gnuradio-windows11-使用（3）离散卷积的结合律证明

书中2.3节介绍了 卷积的 交换律、结合律、分配律。其余的还好，也就是结合律并不是很好证，此外，似乎很多的证明都是用 积分（求和）限是正负无穷来证的，但总觉的这种证明方式不太符合实际，也有点屏蔽细节，因此下面用积分限 k = [0, n]来记录一下：

下面只从 x[n] * (h1(n) * h2(n)) 出发来看，即2.58式左边等于

这里需要注意的是，k1 的积分限是从 0 到 n-k2。

同样的，再看右边，即，2.58式右边等于：

 

这两个等式在写的时候，有个小 trick，就是用卷积的交换律，把 n-k 的项 都放在 h1的内部，因此左右两边再对比的时候，能够统一起来。

这时我们再看E1 和 E2 就会发现，求和的内容完全一致，只有两个积分限不同，即分别是：

• 
• 

这里，如果没记错的话， 在本科教材的《数学物理方法》中似乎有提到，也就是交换求和顺序的方法，用图来看就是：

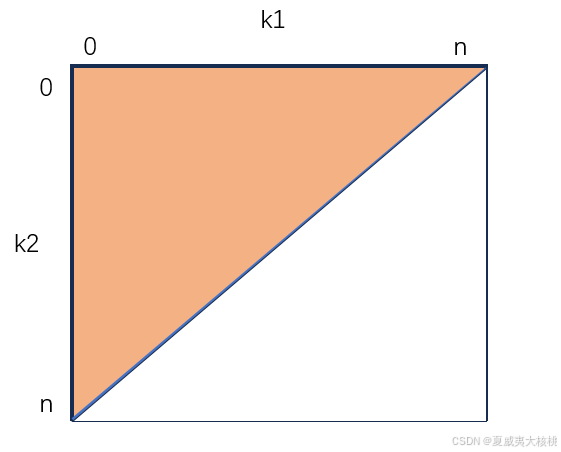
两种求和顺序求的都是橙色面积的三角形，第一个求和是先 k2 再 k1，而第二个求和是先 k1 再 k2 。

说个好理解的，就比如这是一块橘子味的三角蛋糕，不管用刀横着切了，一行一行吃，还是竖着切了，一列一列的吃，最终都能吃完这块蛋糕。

因此，等式左右两边的求和区间 和 求和内容，全部相等，结合律证毕。

如何在 gnuradio 中体现出来，以后再看吧。