深度学习笔记8-逻辑回归

最新推荐文章于 2025-01-29 21:19:09 发布

原创最新推荐文章于 2025-01-29 21:19:09 发布

· 717 阅读

17 ·

版权

文章标签：

#深度学习 #笔记 #逻辑回归

深度学习专栏收录该内容

15 篇文章

订阅专栏

逻辑回归模型

逻辑回归是应用广泛的二分类模型。线性回归模型解决的是回归问题，输出值是连续的实数范围。逻辑回归模型解决的是分类问题，值输出是0或1的离散值。

线性回归假设函数：

$h_{\theta}(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n}$

逻辑回归假设函数：

$h_{\theta}(x)=\frac{1}{1+e^{-(\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n})}}$

逻辑回归在线性回归的基础上增加了sigmoid函数，它也被称为Logistic函数， $g(z)=\tfrac{1}{1+e^{-z}}$ ,sigmoid函数可以将线性计算结果压缩到0-1之间。sigmiod函数，当自变量z趋于负无穷时，函数值趋近于0，当自变量趋于正无穷时，函数值趋近于1。并且sigmoid函数在z=0的位置左右对称。

基于sigmoid函数的性质，可以将线性回归的假设函数放到z的位置即 $z=h_{\theta}(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n}$ ,得到新的函数 $h_{\theta}(x)=\frac{1}{1+e^{-(\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n})}}$ ，该函数就是逻辑回归的假设函数。

逻辑回归和二分类

设逻辑回归模型的输出为 $h_{\theta}(x)$ ,取值范围在0-1之间，可以将它看作是，在给定的输入特征x的情况下，样本属于某个类别的概率。在分类时，会设置一个阈值p，当 $h_{\theta}(x)$ >=p,那么将输入的样本预测为正例，如果 $h_{\theta}(x)$ <p,将输入的样本预测值为负例。根据实际情况可以灵活的设置阈值p，使模型计算出倾向于某种类别的分类结果。

二分类问题的决策边界

决策边界是二分类问题的一个重要概念，决策边界可以是一条直线或一条曲线，前者对应线性分类，后者对应非线性分类。决策边界的形状取决于所使用的分类算法和数据分布。在解决分类问题时，机器算法的目标就寻找合适的决策边界，对数据点进行分类，不同的机器学习算法，对于相同的训练数据会产生不同形状的决策边界。

逻辑回归的决策边界

逻辑回归的假设函数为 $h_{\theta}(x)$ ，先计算线性累加结果 $z=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n}$ ，然后将z输入sigmoid函数 $g(z)=\tfrac{1}{1+e^{-z}}$ ，就得到预测结果h,对于线性方程z,当z=0时，z是n维空间中的平面，该平面将空间中的样本分成两类，分别位于平面两侧。

非线性回归的决策边界

在逻辑回归的假设函数中，z的位置对应一个线性方程，因此逻辑回归属于线性分类器，线性分类器无法直接解决线性不可分的问题。如下图无法使用直线边界进行分类。需要通过曲线对数据点进行分类，这样的曲线就是非线性回归的决策边界。

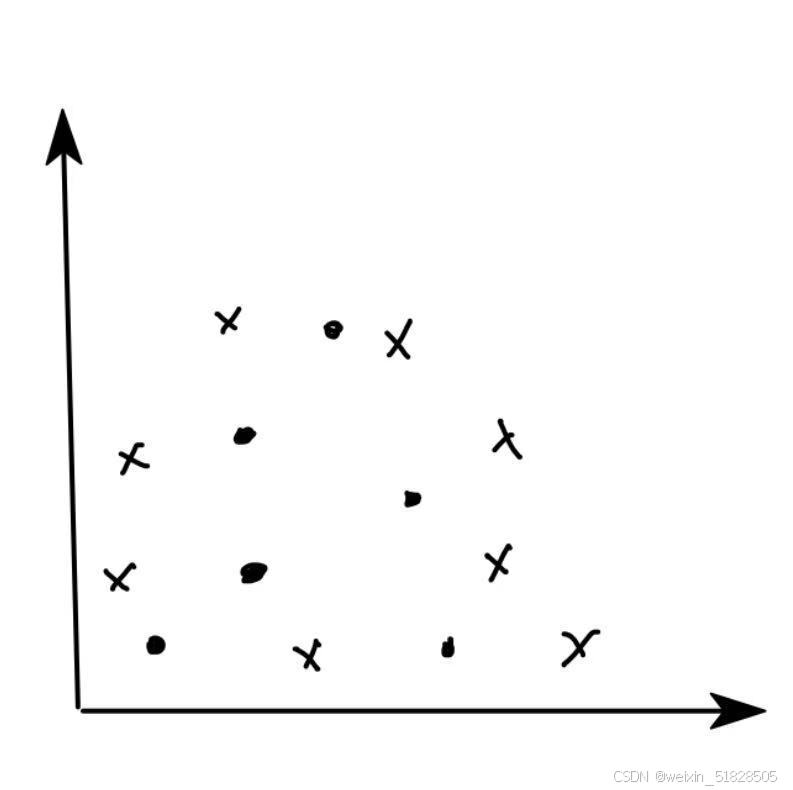
同一分类问题的决策边界不是唯一的，不同的算法会计算出不同的识别方程，就会有不同的决策边界。即使两条决策边界都可以将全部样本识别正确，他们也有好坏之分。对应一些样本分类问题甚至可以找出完全不规则的决策边界，只不过这样的决策边界可能对应的方程 $h_{\theta}(x)$ 会很复杂。在使用方程来表示分类的决策边界时，方程的形式和方程的参数同时决定决策边界的样子。

二元交叉熵损失函数

二元交叉熵损失函数，是用于二分类问题的常用损失函数。这个函数整体衡量了模型的预测概率p，和真实标签y之间的差异。在使用逻辑回归进行二分类时，模型的输出是 $p_{i}=h_{\theta}(x_{i})$ ,代表正样本的预测概率p,因此可以使用二元交叉熵损失函数作为逻辑回归的代价函数，衡量模型预测值 $h_{\theta}(x_{i})$ 和真实值 $y_{i}$ 之间的误差。

$L=-\frac{1}{m}\sum_{i=1}^{m}[y_{i}log(p_{i})+(1-y_{i})log(1-p_{i})]$

$y$ :样本的真实标签， $\in$ {0，1}

$p$ :样本的正例的概率， $\in$ {0，1}

m：训练集中样本的个数

这里log以e为底

线性回归的代价函数使用的是均方误差 $J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x_{i})-y_{i})^{2}$ ,使用均方误差函数可以衡量预测值h和真实值y之间的差异，而对于逻辑回归模型，不能直接使用均方误差。因为逻辑回归的假设函数包含了sigmoid函数，输出的是0-1之间的概率值，如果直接使用均方误差，将 $h_{\theta}(x)$ 带入 $J(\theta)$ 中后，导致 $J(\theta)$ 形成不规则的非凸函数，这种函数很可能会有多个极小值，导致使用梯度下降算法优化函数时，不能找到全局最优解。

分析逻辑回归的代价函数

设 $J(\theta)=\frac{1}{m}\sum_{i=1}^{m}cost(h_{\theta}(x^{i}),y^{i})$ 是逻辑回归模型m个样本的总代价的平均值，定义某一个样本i的代价是 $cost(h_{\theta}(x^{i}),y^{i})$ ，它描述了一个样本的错误值。

我们希望如果某一个样本是正例，标记y=1，此时预测值h越接近0，代价要越大，越接近1，代价越小，相反如果某一个样本是负例，标记y=0，此时预测值h越接近0，代价要越小，越接近1，代价越大。所以设计的cost函数为：

$cost(h_{\theta}(x),y)=\left\{\begin{matrix} -log(h_{\theta}(x)) ,y=1\\ -log(1-h_{\theta}(x)) ,y=0\end{matrix}\right.$ ，

log以e为底

将这两式子合并就得到了逻辑回归的代价函数 $J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}logh_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)})]$

梯度下降求解逻辑回归

逻辑回归模型假设函数： $h_{\theta}(x)=\frac{1}{1+e^{-(\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n})}}$ ,用于逻辑回归模型的预测

逻辑回归模型代价函数： $J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}logh_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)})]$ ，用于衡量全部的m个样本的总误差。

要求的是，使总误差 $J(\theta)$ 取最小值时，模型中的全部参数 $\theta=[\theta_{0},\theta_{1},\theta_{2},...\theta_{n}]^{T}$ ,在这个过程中使用梯度下降算法，进行参数 $\theta$ 的迭代.

求出代价函数在任意一点的梯度向量 $\bigtriangledown J(\theta_{0},\theta_{1}...,\theta_{n})=(\frac{\partial J}{\partial \theta_{0}},\frac{\partial J}{\partial \theta_{1}},...,\frac{\partial J}{\partial \theta_{n}})$

for i in range(0,num)

$\theta_{0}=\theta_{0}-\alpha \frac{\partial J}{\partial \theta_{0}}$ ...

其中对于代价函数 $J(\theta)$ 求得的偏导是： $\frac{\partial J}{\partial \theta_{j}}=\frac{1}{m}\sum_{i=1}^{m}\frac{\partial cost(h_{\theta}(x^{(i)},y^{(i)}))}{\partial \theta_{j}}=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_{j}^{(i)}$