Verilog实现PID控制（跑通带测试案例，不玩虚的）

chen_learning_star

已于 2025-05-19 11:03:18 修改

阅读量485

点赞数 10

CC 4.0 BY-SA版权

分类专栏：高云FPGA 文章标签： fpga开发

于 2025-05-19 10:38:19 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_51352668/article/details/148057692

高云FPGA 专栏收录该内容

3 篇文章

订阅专栏

`PID`的基础知识

自己去补吧，这个很简单，相信大家在做这个的时候PID已经很熟了

`pid_controller.v`模块实现的`pid`控制器

直接先上代码：

module pid_controller (
    input           clk,
    input           rst_n,
    input           pid_en,
    
    input signed [31:0] desired_value,
    input signed [31:0] current_value,
    input [31:0]   Kp,
    input [31:0]   Ki,
    input [31:0]   Kd,

    output          pid_ack,
    output signed [31:0] out
);

// 状态定义
localparam
    IDLE   = 3'b001,       // 空闲状态
    CALC_P = 3'b010,     // 计算比例项
    CALC_I = 3'b011,     // 计算积分项
    CALC_D = 3'b100,     // 计算微分项
    REDUCE = 3'b101,     // 量化处理
    OUTPUT = 3'b110;     // 输出结果

// 寄存器声明
reg [2:0] current_state;
reg [2:0] next_state;
reg signed [31:0] error;            // 当前误差
reg signed [31:0] last_error;       // 上次误差
reg signed [36:0] integral;         // 积分项累加值
reg signed [31:0] p_term;           // 比例项
reg signed [36:0] i_term;           // 积分项
reg signed [31:0] d_term;           // 微分项
reg signed [31:0] p_reduced;        // 量化后的比例项
reg signed [31:0] i_reduced;        // 量化后的积分项
reg signed [31:0] d_reduced;        // 量化后的微分项
reg signed [31:0] pid_output;       // PID输出

// 状态机主逻辑
always @(posedge clk or negedge rst_n) begin
    if (!rst_n) begin
        current_state <= IDLE;
        error <= 0;
        last_error <= 0;
        integral <= 0;
        p_term <= 0;
        i_term <= 0;
        d_term <= 0;
        p_reduced <= 0;
        i_reduced <= 0;
        d_reduced <= 0;
        pid_output <= 0;
    end else begin
        current_state <= next_state;
        
        case (current_state)
            IDLE: begin
                if (pid_en) begin
                    error <= desired_value - current_value;
                end
            end
            
            CALC_P: begin
                p_term <= error * Kp;
            end
            
            CALC_I: begin
                // 抗积分饱和处理
                if (!((integral > 2000 && error > 0) || 
                     (integral < -2000 && error < 0))) begin
                    integral <= integral + error;
                end
                i_term <= integral * Ki;
            end
            
            CALC_D: begin
                d_term <= (error - last_error) * Kd;
                last_error <= error;
            end
            
            REDUCE: begin
                // 右移7+右移9 ≈ 除以102.4
                p_reduced <= (p_term >>> 7) + (p_term >>> 9);
                i_reduced <= (i_term >>> 7) + (i_term >>> 9);
                d_reduced <= (d_term >>> 7) + (d_term >>> 9);
            end
            
            OUTPUT: begin
                pid_output <= p_reduced + i_reduced + d_reduced;
                // 可以在这里添加输出限幅逻辑
            end
        endcase
    end
end

// 状态转移逻辑
always @(*) begin
    case (current_state)
        IDLE:   next_state = pid_en ? CALC_P : IDLE;
        CALC_P: next_state = CALC_I;
        CALC_I: next_state = CALC_D;
        CALC_D: next_state = REDUCE;
        REDUCE: next_state = OUTPUT;
        OUTPUT: next_state = IDLE;
        default: next_state = IDLE;
    endcase
end

// 输出赋值
assign out = pid_output;
assign pid_ack = (current_state == OUTPUT);

endmodule

需要注意的点，注意按情况改变error <= desired_value - current_value; 的顺序，如果仿真的时候控制器输出out出现不正常的值，那么应该换一下顺序；
一般是按照流水线计算输出的，因为首先思路清晰，其次，可以避免在一个时钟周期内干很多事情，比如一堆的乘法，如果加入乘法器的ip核，那么可以实现节约资源，每次复用一个乘法单元；

注意下面的地方：

  	p_reduced <= (p_term >>> 7) + (p_term >>> 9);
      i_reduced <= (i_term >>> 7) + (i_term >>> 9);
      d_reduced <= (d_term >>> 7) + (d_term >>> 9);

这里的意思是把传进来的kp、ki、kd都进行缩小，这个具体原因可以deepseek

测试案例（相信初学的人这里最头疼）

直接上代码：

`timescale 1ns/1ps

module tb_pid_controller;
    reg clk;
    reg rst_n;
    reg pid_en;
    wire pid_ack;
    reg signed [31:0] desired_value;
    reg signed [31:0] current_value;
    reg [31:0] Kp;
    reg [31:0] Ki;
    reg [31:0] Kd;
    wire signed [31:0] out;
    
    //假设一个模型，用来和pid控制器形成闭环   
    always @(posedge clk or negedge rst_n) begin
        if (!rst_n) begin
            desired_value <= 0;
            current_value <= 0;
        end
        else if (pid_ack) begin
            current_value <= current_value + (out >>> 4);
        end
    end
    
    //初始化pid模块
    pid_controller uut (
        .clk(clk),
        .rst_n(rst_n),
        .pid_en(pid_en),
        .desired_value(desired_value),
        .current_value(current_value),
        .Kp(Kp),
        .Ki(Ki),
        .Kd(Kd),
        .pid_ack(pid_ack),
        .out(out)
    );
    
    //模拟时钟
    initial begin
        clk = 0;
        forever #10 clk = ~clk;
    end
    
    //初始化
    initial begin
        clk = 1'b0;
        rst_n <= 1'b0;
        pid_en <= 1'b0;
        desired_value <= 0;
        current_value <= 0;
        Kp <= 32'd100;  // Proportional gain
        Ki <= 32'd5;    // Integral gain
        Kd <= 32'd2;    // Derivative gain
        
        // Apply reset
        #20;
        rst_n <= 1'b1;
        
        #20;
        desired_value <= 1000;
        pid_en <= 1'b1;
        
    end
    
endmodule

注意你为什么有的时候会测试失败（本人也踩了几天的坑），因为你一定要等到pid_controller.v模块计算好了out之后再更新模型的信息，随便假设一模型测试一下，比如最简单的积分模型current_value <= current_value + (out >>> 4);也就是：

//假设一个模型，用来和pid控制器形成闭环   
   always @(posedge clk or negedge rst_n) begin
       if (!rst_n) begin
           desired_value <= 0;
           current_value <= 0;
       end
       else if (pid_ack) begin//只有当控制器算出来可以用的时候更新
           current_value <= current_value + (out >>> 4);
       end
   end

modelsim测试结果

仿真结果

此时你很皮，想的是，为什么都测试一个不变的值呢，万一目标是`sin`这种变动的呢，有没有变动的值呢，有的`xd`，有的`xd`，哎，我一下是定值`1000`，稳定后一下改变为`sin`图像

直接上代码：

`timescale 1ns/1ps

module tb_pid_controller;
    reg clk;
    reg rst_n;
    reg pid_en;
    wire pid_ack;
    reg signed [31:0] desired_value;
    reg signed [31:0] current_value;
    reg [31:0] Kp;
    reg [31:0] Ki;
    reg [31:0] Kd;
    wire signed [31:0] out;
    



    //假设一个模型，用来和pid控制器形成闭环   
    always @(posedge clk or negedge rst_n) begin
        if (!rst_n) begin
            desired_value <= 0;
            current_value <= 0;
        end
        else if (pid_ack) begin
            current_value <= current_value + (out >>> 4);
        end
    end
    
    // 正弦波生成变量
    real sin_phase = 0;
    real sin_step;
    reg desired_value_sin_flag; // 标志着期望轨迹从期望值变为期望的sin图像
    // 正弦波期望值
    initial begin
        sin_step = 2 * 3.1415926 / (20000 / 10);
    end
    always @(posedge clk) begin
        if (desired_value_sin_flag) begin
            sin_phase <= sin_phase + sin_step;
            if (sin_phase >= 2 * 3.1415926) begin
                sin_phase <= sin_phase - 2 * 3.1415926;
            end
            desired_value <= $floor(1000 * $sin(sin_phase));
        end
        
    end

    //初始化pid模块
    pid_controller uut (
        .clk(clk),
        .rst_n(rst_n),
        .pid_en(pid_en),
        .desired_value(desired_value),
        .current_value(current_value),
        .Kp(Kp),
        .Ki(Ki),
        .Kd(Kd),
        .pid_ack(pid_ack),
        .out(out)
    );
    
    //模拟时钟
    initial begin
        clk = 0;
        forever #10 clk = ~clk;
    end
    

    
    //初始化
    initial begin
        clk = 1'b0;
        rst_n <= 1'b0;
        pid_en <= 1'b0;
        desired_value <= 0;
        current_value <= 0;

        desired_value_sin_flag <= 0;

        Kp <= 32'd100;  // Proportional gain
        Ki <= 32'd5;    // Integral gain
        Kd <= 32'd2;    // Derivative gain
        
        // Apply reset
        #20;
        rst_n <= 1'b1;
        
        #20;
        desired_value <= 1000;
        pid_en <= 1'b1;


        # 20000 //注意这里的话我已经测试了desired_value <= 1000;，是20000ns的时候收敛了，这时候才开始sin的图形
        desired_value_sin_flag <= 1;//期望轨迹变为了sin图形
    end
    
endmodule

相比于前面的测试案例只增加了：

    // 正弦波生成变量
    real sin_phase = 0;
    real sin_step;
    reg desired_value_sin_flag; // 标志着期望轨迹从期望值变为期望的sin图像
    // 正弦波期望值
    initial begin
        sin_step = 2 * 3.1415926 / (20000 / 10);
    end
    always @(posedge clk) begin
        if (desired_value_sin_flag) begin
            sin_phase <= sin_phase + sin_step;
            if (sin_phase >= 2 * 3.1415926) begin
                sin_phase <= sin_phase - 2 * 3.1415926;
            end
            desired_value <= $floor(1000 * $sin(sin_phase));
        end
        
    end

以及用一个标志位desired_value_sin_flag标记期望值发生了变化

   # 20000 //注意这里的话我已经测试了desired_value <= 1000;，是20000ns的时候收敛了，这时候才开始sin的图形
        desired_value_sin_flag <= 1;//期望轨迹变为了sin图形

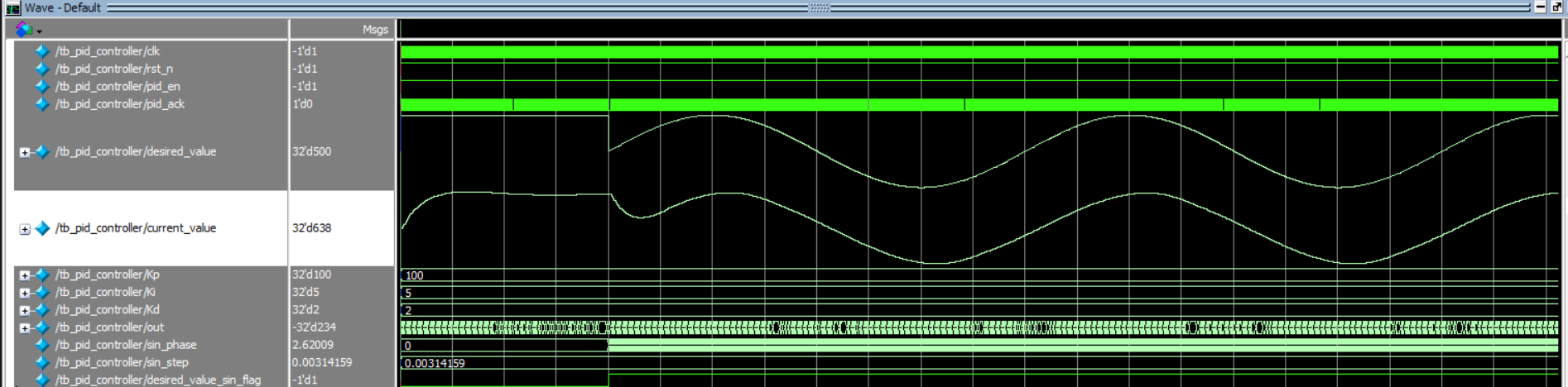
仿真结果

在这里插入图片描述

Verilog实现PID控制（跑通带测试案例，不玩虚的）

PID的基础知识

pid_controller.v模块实现的pid控制器

测试案例（相信初学的人这里最头疼）

modelsim测试结果

此时你很皮，想的是，为什么都测试一个不变的值呢，万一目标是sin这种变动的呢，有没有变动的值呢，有的xd，有的xd，哎，我一下是定值1000，稳定后一下改变为sin图像

仿真结果

`PID`的基础知识

`pid_controller.v`模块实现的`pid`控制器

此时你很皮，想的是，为什么都测试一个不变的值呢，万一目标是`sin`这种变动的呢，有没有变动的值呢，有的`xd`，有的`xd`，哎，我一下是定值`1000`，稳定后一下改变为`sin`图像