递归与回溯解决数组元素组合问题-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_51117061/article/details/123565375

复盘：你重点是思考如何实现一种交互，而绝对不是单独的解题，从效用的角度出发，还是需要提醒一下，所以重点是如何产出问题，如何实现交互——预设有结果的问题，欲擒故纵

最接近的一个题目
首先题目进行对比，都是使得数字和为一个定值的（target和n），只不过此处没有固定下元素的位置，而我们的题目固定了元素只能是m个，这既是简单，也是不简单，一方面如果少了直接补0节课，另一方面如果多了，则该组合应该被舍弃
可不可以重复选取，此处是可以重复的，两者都是可以重复的

树本身的逻辑就是一种迭代
如果给你做，你会如何操作，然后实现一种对比

可以给数组candidates设定一个元素数量i
然后对其遍历，虽然此处我们并没有什么要求，但是可以实现逐个往后的存取操作
我们使用递归的结构
不对 candidates内部的选项应该是遍历的，比如在我们的题目中对应的是m个，在这里对应的是一个固定的；但是我们需要用i去记录的我们的新数组比如select[i]，每取一个就存入其中，在我们的那道题中，i有m个

select[i]=candidates[j]-j实现一轮遍历
target=target-candidates[i]
话说candidates[i]具体取什么是都要遍历一遍吗，这个树的遍历时如何操作的-是的，回答见上

返回和循环什么结构？

begin是什么意思，为什么要仿照树结构，如何实现遍历，提取candidates[i]中的元素呢?
在这里，遍历被翻译为搜索，利用堆栈的树结构

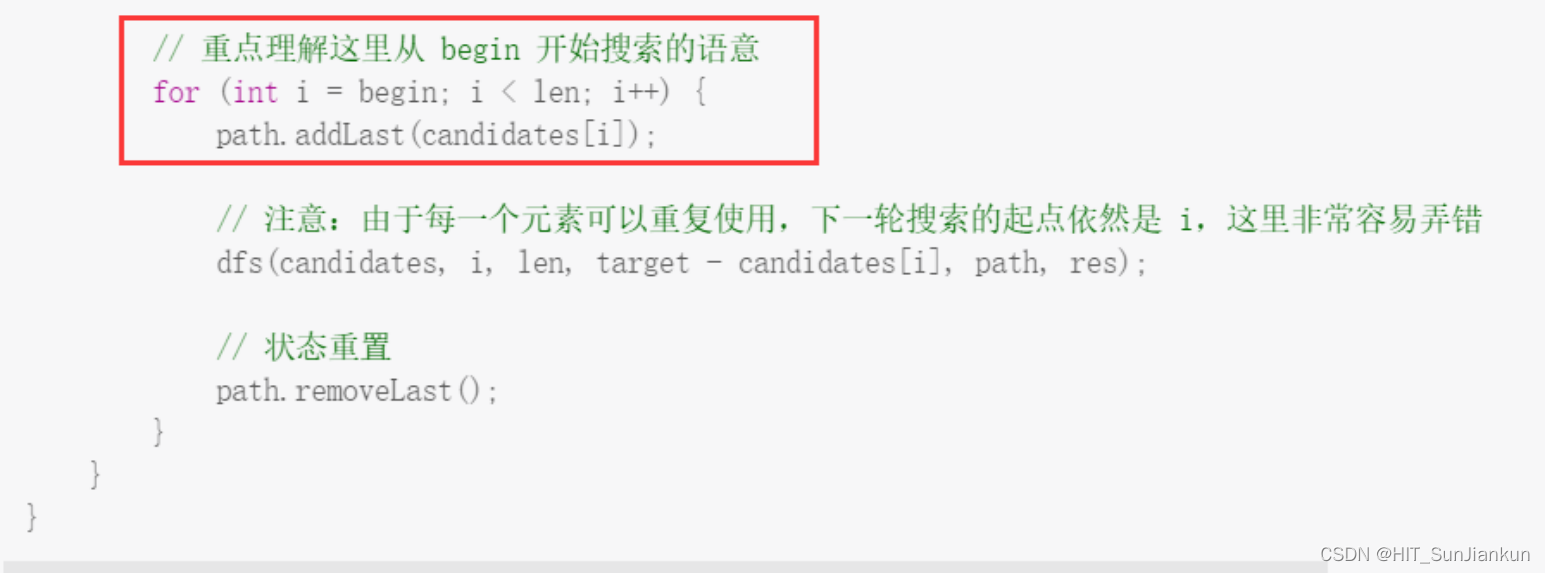
res是一个集，方便收集存储与导出；path是一个栈，路径，方便检索与遍历

感觉两种做法，dfs和backtrack，那么接下来考虑如何就将该写法修改我们可以跑通的下一个程序，差异在哪里，我们的题目是什么？

题目：设置一个数组，里边可以装在m个数字，其中每个数字都可以任意选取0到n的任意整数，并且需要保证容器数组的元素之和为n

可以把target=n看成一段绳子，然后取进行m-1端分割，但是后面怎么采取的操作，达到了什么样的效果，我还没有太注意——可以到时候多关注下那个帖子

直接对比差异，就可以完成填充了
注意：永远要小心最后一步的差异，不到最后不放松

差别在于
步长限定为m
candidates固定为0,1,2,...,n
target=n
如果步长少于m这道改进算法说的有道理，你有没有考虑重复啊，就是这个向量包含顺序的因素吗？
——我们假设的应该是有顺序的向量，所以应该是不考虑的？那这里面还能够适用吗，他有没有删去好像差不多的情况？
我感觉第一个并没有解决这个再列表中担心的额重复问题啊，感觉跟向量是同样的一套解法就停了，则后面都补充0,；如果步长多于m，则即刻停止