verilog典型电路设计之Wallace 树乘法器
Wallace 树乘法器
是一种我们在集成电路学习中应用非常广泛的设计 其中由两部分组成 一个是FA和HA
FA是full add 全加器 HA 是half 半加器
加法从数据最密集的地方开始,不断地反复使用全加器半加器来覆盖“树” 。 这一级全加器 是一个3输入2输出的器件,因此全加器又称为3-2压缩器。通过全加器将树的深度不断缩减,最终缩减为一个深度为2的树。最后一级则采用一个简单的两输入加法器组成。
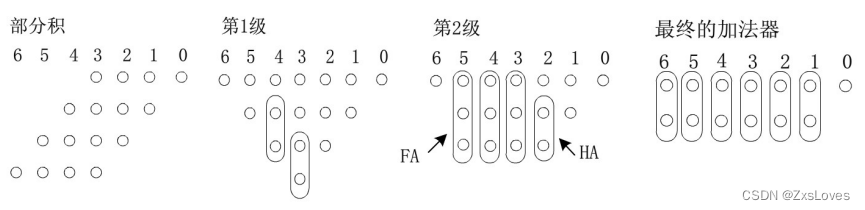

我们所非常熟知的常规算法是印象里 几个数加起来 一种做法是把其中的一个个数添加,依次相乘 然后慢慢算出它最终的结果 还有一种做法是我们按照常规的竖式加算的方法 我们按照小学教的

借用一下上次的图 我们会很清晰的发现 乘算之后会得到4个这种暂态的数
好因为这是4位数乘4位数 要是我们把想法扩大 把目标放在更大的数乘更大的数呢 我们会遇到 更大层次的数相乘 那么就会余下好几层的数乘 我们先引入 全加器的概念将三位数压缩成2位
我就以上面的数相加进行举例
比如说1 2 3 4 组数字 我挑选 1 2 3 组我现在想把他压缩成2位 就是

就是我们将三位数字可以拆解成1个十位 1个个位 就像是1+1+1=11
0+0+1=01 这就是全加器的实现 我们可以把 三个数字 变成 两个数字
而对于半加器来说是 只有两位数相加才会得到结果的
就好比最大的 1+1 =10
这里所有的加数都是以二进制的形式存在的
下面是wallace的verilog代码
module wallace(x,y,out);
parameter size=4;
input [size-1:0] x,y;
output [2*size-1:0] out;
wire [size*size-1:0] a;
wire [1:0] b0,b1,c0,c1,c2,c3;
wire [5:0] add_a,add_b;
wire [6:0] add_out;
wire [2*size-1:0] out;
assign a={x[3],×[3],×[2],x[2],x[1],x[3],x[1],x[0],×[3],×[2],x[1],×[0],×[2],×[1],×[0],×[O]}&
{y[3].y[2].y[3].y[2],y[3].y[1].y[2].y[3].y[0].y[1].y[1],.y[2],.y[0].y[0].y[1].y[0]};
multiplierhadd U1(.x(a[8]),.y(a[9]),.out(b0));
hadd U2(.x(a[11]),y(a[12]),.out(b1));
hadd U3(.x(a[4]),-y(a[5]),.out(c0));
fadd U4(.x(a[6]),-y(a[7]),z(b0[0]),.out(c1));
fadd U5(.x(a[13]),-y(a[14]),z(b0[1]),.out(c2));
fadd U6(.x(b1[0])..y(a[10]),z(b1[1]),.out(c3));
assign add_a={c3[1],c2[1],c1[1],cO[1],a[3],a[1l;lladderassign add_b={a[15],c3[0],c2[0],c1[0],c0[0],a[2]};
assign add_out=add_a+add_b;
assign out={add_out,a[0]};
endmodule
module fadd(x,y, z, out);
output [1:0]out;
input x,y,z;
assign out=x+y+z;
endmodule
module hadd(x, y, out);
output [1:0]out;
input x,y;
assign out=x+y;
endmodule
下面是wallace的testbench
module wallace_tb;
reg [3:0] x, y;
wire [7:0] out;
wallace m(.x(x),.y(y),.out(out));
initial
begin
x=3;y=4;
#20 x=2; y=3;
#20 x=6; y=8;
end
endmodule





 本文详细介绍了Verilog语言中Wallace树乘法器的设计,包括FA(全加器)和HA(半加器)的作用,以及如何通过全加器和半加器构建一个多级的压缩乘法结构。测试bench示例展示了如何在Verilog中实现和测试这个乘法器模块。
本文详细介绍了Verilog语言中Wallace树乘法器的设计,包括FA(全加器)和HA(半加器)的作用,以及如何通过全加器和半加器构建一个多级的压缩乘法结构。测试bench示例展示了如何在Verilog中实现和测试这个乘法器模块。
















 670
670

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








