二叉树的基本概念和性质
二叉树是一种重要的数据结构,在计算机科学和数学中都有广泛的应用。它由一组节点组成,其中每个节点都可以具有零个、一个或两个子节点,而且子节点之间存在特定的关系。下面介绍二叉树的基本概念和性质。
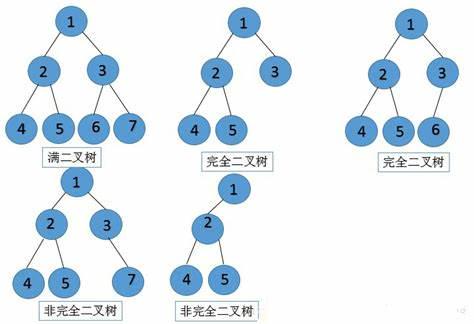
定义
二叉树是一种树形结构,其每个节点最多有两个子节点,分别称为左子节点和右子节点。如果左子节点不为空,则左子节点的值小于或等于其父节点的值;如果右子节点不为空,则右子节点的值大于或等于其父节点的值。
术语
根节点:二叉树的最上面一个节点称为根节点。
叶子节点:没有子节点的节点称为叶子节点或终端节点。
内部节点:有至少一个子节点的节点称为内部节点或非终端节点。
子树:根节点及其所有子孙节点构成的树称为子树。
左子树:某个节点的左子节点及其所有子孙节点构成的树称为左子树。
右子树:某个节点的右子节点及其所有子孙节点构成的树称为右子树。
性质
一个二叉树最多有 2^h - 1 个节点,其中 h 是树的高度。
一棵深度为 h 的二叉树最多有 2^(h+1) - 1 个节点。
在二叉树的第 i 层上最多有 2^(i-1) 个节点。
如果一棵二叉树的叶子节点数为 n0,度为 2 的节点数为 n2,则 n0 = n2 + 1。
在一棵有 n 个节点的完全二叉树中,如果节点按层次编号(根节点为第 1 层),则对于任意的 i,有:
如果 i = 1,则节点 i 是二叉树的根节点。
如果 i > 1,则节点 i 的父节点是节点 i/2。
如果 2i ≤ n,则节点 i 的左子节点是节点 2i。
如果 2i+1 ≤ n,则节点 i 的右子节点是节点 2i+1。
这些基本概念和性质是理解和使用二叉树的基础,可以作为写博客的框架来介绍二叉树。
实现二叉树的基本操作
创建二叉树:可以通过递归或循环方式创建二叉树,其中递归方式较为常用。递归方式可以先读入根节点,然后递归创建左子树和右子树。
遍历二叉树:可以通过前序遍历、中序遍历和后序遍历三种方式遍历二叉树。其中前序遍历的顺序是先访问根节点,然后依次访问左子树和右子树;中序遍历的顺序是先访问左子树,然后访问根节点,最后访问右子树;后序遍历的顺序是先访问左子树,然后访问右子树,最后访问根节点。
查找二叉树节点:可以通过递归方式查找二叉树节点,若当前节点不是目标节点,则递归查找左子树和右子树。
插入二叉树节点:可以通过递归方式插入二叉树节点,先找到插入位置,然后递归创建左子树和右子树。
删除二叉树节点:可以通过递归方式删除二叉树节点,先找到目标节点,然后根据其子节点的情况分别进行处理。
代码实现
public class BinaryTree<T> {
private TreeNode<T> root;
private static class TreeNode<T> {
T val;
TreeNode<T> left;
TreeNode<T> right;
TreeNode(T val) {
this.val = val;
}
}
public void insert(T val) {
root = insert(root, val);
}
private TreeNode<T> insert(TreeNode<T> node, T val) {
if (node == null) {
return new TreeNode<>(val);
}
if (val.hashCode() < node.val.hashCode()) {
node.left = insert(node.left, val);
} else if (val.hashCode() > node.val.hashCode()) {
node.right = insert(node.right, val);
}
return node;
}
public boolean contains(T val) {
return contains(root, val);
}
private boolean contains(TreeNode<T> node, T val) {
if (node == null) {
return false;
}
if (val.hashCode() == node.val.hashCode()) {
return true;
} else if (val.hashCode() < node.val.hashCode()) {
return contains(node.left, val);
} else {
return contains(node.right, val);
}
}
public void remove(T val) {
root = remove(root, val);
}
private TreeNode<T> remove(TreeNode<T> node, T val) {
if (node == null) {
return null;
}
if (val.hashCode() == node.val.hashCode()) {
if (node.left == null && node.right == null) {
return null;
}
if (node.left == null) {
return node.right;
}
if (node.right == null) {
return node.left;
}
TreeNode<T> tmp = node.right;
while (tmp.left != null) {
tmp = tmp.left;
}
node.val = tmp.val;
node.right = remove(node.right, tmp.val);
} else if (val.hashCode() < node.val.hashCode()) {
node.left = remove(node.left, val);
} else {
node.right = remove(node.right, val);
}
return node;
}
public void printTree() {
if (root == null) {
return;
}
Queue<TreeNode<T>> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode<T> node = queue.poll();
System.out.print(node.val + " ");
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
System.out.println();
}
}这个实现只涉及到二叉树的基本操作,包括插入、查找、删除和打印。其中,插入操作根据节点值的哈希码进行比较,小于当前节点值的插入到左子树,大于当前节点值的插入到右子树。查找操作也是基于哈希码进行比较,删除操作则涉及到删除节点后重新构建二叉树。打印操作是基于层次遍历实现的。
二叉搜索树
二叉搜索树(Binary Search Tree,BST)是一种特殊的二叉树,它具有以下性质:
每个节点都存储一个值。
对于任意节点,其左子树中的所有节点的值都小于该节点的值,而右子树中的所有节点的值都大于该节点的值。
左子树和右子树都是二叉搜索树。
因此,二叉搜索树是一种具有有序性的数据结构,它支持快速的查找、插入和删除操作。对于一个有序的序列,我们可以通过构建二叉搜索树来对其进行排序,这也是二叉搜索树的一种常见应用。
二叉搜索树的时间复杂度取决于其高度,如果二叉搜索树的高度为 $h$,则最坏的时间复杂度为 $O(h)$。在最好的情况下,当二叉搜索树是平衡树时,它的高度为 $\log n$,此时查找、插入和删除的时间复杂度均为 $O(\log n)$。但是,如果二叉搜索树是不平衡的,例如退化成一条链的情况,其时间复杂度将退化为 $O(n)$。
因此,在实际应用中,为了保证二叉搜索树的高度尽可能地小,我们通常会采用平衡树的实现方式,例如红黑树、AVL树等。
public class BinarySearchTree<T extends Comparable<T>> {
private Node root;
private class Node {
T value;
Node left;
Node right;
Node(T value) {
this.value = value;
}
}
// 插入节点
public void insert(T value) {
root = insert(root, value);
}
private Node insert(Node node, T value) {
if (node == null) {
return new Node(value);
}
int cmp = value.compareTo(node.value);
if (cmp < 0) {
node.left = insert(node.left, value);
} else if (cmp > 0) {
node.right = insert(node.right, value);
} else {
node.value = value;
}
return node;
}
// 查找节点
public boolean contains(T value) {
return contains(root, value);
}
private boolean contains(Node node, T value) {
if (node == null) {
return false;
}
int cmp = value.compareTo(node.value);
if (cmp < 0) {
return contains(node.left, value);
} else if (cmp > 0) {
return contains(node.right, value);
} else {
return true;
}
}
// 删除节点
public void remove(T value) {
root = remove(root, value);
}
private Node remove(Node node, T value) {
if (node == null) {
return null;
}
int cmp = value.compareTo(node.value);
if (cmp < 0) {
node.left = remove(node.left, value);
} else if (cmp > 0) {
node.right = remove(node.right, value);
} else {
if (node.left == null) {
return node.right;
} else if (node.right == null) {
return node.left;
} else {
Node minNode = findMin(node.right);
node.value = minNode.value;
node.right = remove(node.right, minNode.value);
}
}
return node;
}
private Node findMin(Node node) {
while (node.left != null) {
node = node.left;
}
return node;
}
}这里实现了二叉搜索树的插入、查找、删除操作。其中插入和查找操作都是比较简单的递归实现,而删除操作稍微复杂一些,需要考虑被删除节点的子树的情况。
平衡二叉树
平衡二叉树(Balanced Binary Tree),也叫AVL树,是一种特殊的二叉搜索树。在平衡二叉树中,任何一个节点的左右子树的高度差不超过1,这保证了树的高度始终在log(n)级别,提高了树的查找效率。
平衡二叉树具有以下性质:
树中任意一个节点的左右子树的高度差不超过1;
平衡二叉树是一棵空树,或它的左右两个子树的高度差的绝对值不超过1,且左右两个子树都是一棵平衡二叉树。
常见的平衡二叉树有AVL树、红黑树、替罪羊树、Treap等。
在平衡二叉树中,因为每个节点的左右子树高度差不超过1,因此对于任意一个节点,它的左子树和右子树的高度最多相差1。因此,我们可以将左子树的高度和右子树的高度都记录下来,并将它们的差值称为平衡因子。
当插入或删除节点后,如果导致某个节点的平衡因子的绝对值大于1,则需要通过旋转操作将其调整平衡。常见的旋转操作有左旋和右旋两种,它们的具体实现可以根据平衡二叉树的类型而有所不同。
下面是一个简单的Java代码实现平衡二叉树的基本操作(以AVL树为例):
class Node {
int val, height;
Node left, right;
Node(int val) {
this.val = val;
height = 1;
}
}
class AVLTree {
Node root;
// 计算节点高度
int height(Node node) {
if (node == null)
return 0;
return node.height;
}
// 获取节点的平衡因子
int getBalance(Node node) {
if (node == null)
return 0;
return height(node.left) - height(node.right);
}
// 右旋转
Node rightRotate(Node y) {
Node x = y.left;
Node t2 = x.right;
x.right = y;
y.left = t2;
// 更新高度
y.height = Math.max(height(y.left), height(y.right)) + 1;
x.height = Math.max(height(x.left), height(x.right)) + 1;
return x;
}
// 左旋转
Node leftRotate(Node x) {
Node y = x.right;
Node t2 = y.left;
y.left = x;
x.right = t2;
// 更新高度
x.height = Math.max(height(x.left), height(x.right)) + 1;
y.height = Math.max(height(y.left), height(y.right)) + 1;
return y;
}
// 插入节点
Node insert(Node node, int val) {
// 执行标准的BST插入
if (node == null)
return new Node(val);
if (val < node.val)
node.left = insert(node.left, val);
else if (val > node.val)
node.right = insert(node.right, val);
else
return node;
// 更新高度
node.height = 1 + Math.max(height(node.left), height(node.right));
// 获取平衡因子
int balance = getBalance(node);
// LL情况,需要右旋转
if (balance > 1 && val < node.left.val)
return rightRotate(node);
// RR情况,需要左旋转
if (balance < -1 && val > node.right.val)
return leftRotate(node);
// LR情况,需要先左旋再右旋
if (balance > 1 && val > node.left.val) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// RL情况,需要先右旋再左旋
if (balance < -1 && val < node.right.val) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
// 中序遍历
void inorderTraversal(Node node) {
if (node != null) {
inorderTraversal(node.left);
System.out.print(node.val + " ");
inorderTraversal(node.right);
}
}
}
public class Main {
public static void main(String[] args) {
AVLTree<Integer> tree = new AVLTree<Integer>();
tree.insert(5);
tree.insert(10);
tree.insert(15);
tree.insert(20);
tree.insert(25);
tree.insert(30);
tree.insert(35);
tree.insert(40);
System.out.println("Inorder traversal of AVL tree:");
tree.inorder();
System.out.println("\n\nLevel order traversal of AVL tree:");
tree.levelOrder();
System.out.println("\n\nDeleting 20 from AVL tree:");
tree.delete(20);
System.out.println("\n\nInorder traversal of AVL tree after deletion:");
tree.inorder();
System.out.println("\n\nLevel order traversal of AVL tree after deletion:");
tree.levelOrder();
}
}
public class AVLTree<T extends Comparable<T>> {
private Node<T> root;
private int height(Node<T> node) {
if (node == null) {
return 0;
} else {
return node.getHeight();
}
}
private int getBalance(Node<T> node) {
if (node == null) {
return 0;
} else {
return height(node.getLeft()) - height(node.getRight());
}
}
private Node<T> rotateRight(Node<T> y) {
Node<T> x = y.getLeft();
Node<T> T2 = x.getRight();
x.setRight(y);
y.setLeft(T2);
y.setHeight(Math.max(height(y.getLeft()), height(y.getRight())) + 1);
x.setHeight(Math.max(height(x.getLeft()), height(x.getRight())) + 1);
return x;
}
private Node<T> rotateLeft(Node<T> x) {
Node<T> y = x.getRight();
Node<T> T2 = y.getLeft();
y.setLeft(x);
x.setRight(T2);
x.setHeight(Math.max(height(x.getLeft()), height(x.getRight())) + 1);
y.setHeight(Math.max(height(y.getLeft()), height(y.getRight())) + 1);
return y;
}
private Node<T> minValueNode(Node<T> node) {
Node<T> current = node;
while (current.getLeft() != null) {
current = current.getLeft();
}
return current;
}
private Node<T> insert(Node<T> node, T data) {
if (node == null) {
return new Node<>(data);
}
int cmp = data.compareTo(node.data);
if (cmp < 0) {
node.left = insert(node.left, data);
} else if (cmp > 0) {
node.right = insert(node.right, data);
} else {
return node;
}
// 更新节点的高度
node.height = Math.max(height(node.left), height(node.right)) + 1;
// 计算平衡因子
int balanceFactor = getBalanceFactor(node);
// 如果节点不平衡,进行平衡操作
if (balanceFactor > 1) {
// LL型:右旋
if (getBalanceFactor(node.left) >= 0) {
return rightRotate(node);
} else { // LR型:左旋+右旋
node.left = leftRotate(node.left);
return rightRotate(node);
}
} else if (balanceFactor < -1) {
// RR型:左旋
if (getBalanceFactor(node.right) <= 0) {
return leftRotate(node);
} else { // RL型:右旋+左旋
node.right = rightRotate(node.right);
return leftRotate(node);
}
}
return node;
}堆和优先队列
堆(Heap)是一种特殊的树状数据结构,它是一个完全二叉树,其中父节点的键值总是大于或等于任何一个子节点的键值(最大堆),或者小于或等于任何一个子节点的键值(最小堆)。由于这个性质,堆被广泛应用于排序、优先队列、图形数据结构等领域。
优先队列(Priority Queue)是一种抽象数据类型,它是一种特殊的队列,其中每个元素都有一个优先级。元素按照优先级依次被插入到队列中,当从队列中弹出元素时,总是弹出优先级最高的元素。
堆可以用于实现优先队列。堆排序的核心思想就是通过构建一个堆来实现排序,而优先队列可以通过使用堆来实现元素的插入和删除。具体来说,对于最大堆,优先队列的最大元素就是堆的根节点;对于最小堆,优先队列的最小元素就是堆的根节点。
Java中提供了优先队列的实现类PriorityQueue,它是通过堆来实现的。可以使用PriorityQueue实现元素的插入、删除和查找最大/最小元素等操作。堆和优先队列在算法和数据结构中都具有重要的应用价值。
在数据结构中,二叉树、平衡二叉树、堆和优先队列都是非常重要的概念和数据结构。通过了解它们的基本概念和操作,我们可以更好地应用它们解决实际问题。同时,掌握这些数据结构的实现原理和时间复杂度也是很重要的,可以帮助我们更好地进行算法分析和设计。希望这篇博文能够为你提供一些帮助。























 2286
2286

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








