随机森林

什么是随机森林？

随机森林是在决策树的基础上衍生出来的。决策树和随机森林的关系就是树和森林的关系。通过对原始训练样本的抽样，以及对特征节点的选择，我们可以得到许多棵不同的树。

构造决策树：信息增益或者基尼算法。决策树算法很直观，且易于理解，而且它和我们通常决策思考的习惯基本契合，这些都是它的优点，但是同样它的缺点也很明显。对于多特征的复合分类问题，它的效率往往就不会很高，而且极易过拟合。

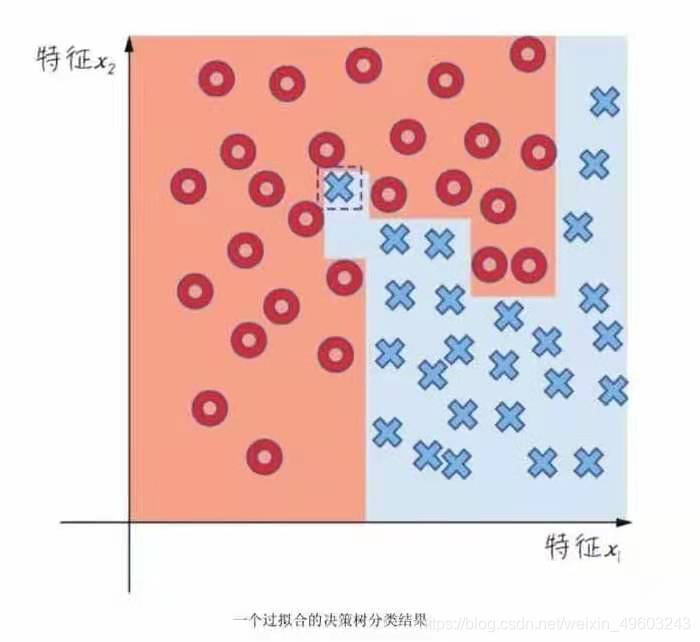
当树的节点很深时，容易学习到高度不规则的模式造成较大的方差，泛化能力弱 。

随机森林就相当于决策树经过集成后的升级版本。

随机森林的基本思路就是把很多棵决策树的结果集成起来，避免过拟合，同时提高准确率。其中每一棵树都是在原始数据集当中抽取不同子集进行训练，这样做虽然单独的一棵决策树它的预测偏差可能会有小幅度增加，但是进行综合平均之后，模型性能会大大地提升。

 算法核心：或许每棵树都是一个糟糕的预测器，但是集中起来可以得到一个很好的模型。决策树的数量越大，随机森林的精确度越高。

构造随机森林（假设数据集包括了n个训练样本，特征维度是m）

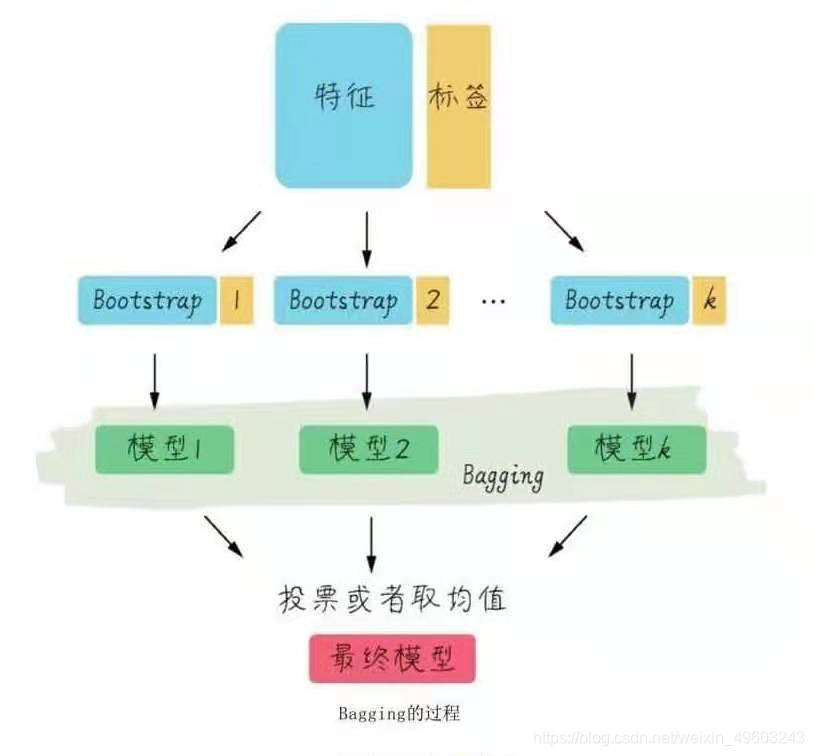
从原始样本集中通过随机抽取形成k个训练集，每轮抽取个训练q个样本，（有放回抽取），这k个训练集彼此独立，这一过程就是bootstrap

每次使用一个训练集通过相同的机器学习算法（如决策树）得到一个模型。k个训练集得到k个模型（基模型）

对多棵决策树进行bagging

给定一个新的识别对象，随机森林中的每一课树都会根据这个对象的属性得出一个分类结果，然后我们把这些分类结果以投票的形式保存下来，随机森林选出票数最高的分类结果作为这个森林的分类结果。

而在回归问题中，我们把每一棵树的输出进行平均得到结果。

(bagging是一种集成学习算法，是bootstrap aggregating的缩写，有些地方会叫做套袋法，袋装法，自助聚合。)

随机森林的优点：1.既可以用于分类，也可以用于回归问题。分类：即使有部分数据缺失，随机森林也可以保持很高的分类精度。而且可以防止过拟合。

缺点：在噪声过大的分类和处理回归问题时还是容易过拟合.

它像一个黑箱，很难控制它的行为.相比于单一决策树，它的随机性让我们难以对模型进行解释

随机森林的运用：

1银行利用随机森林寻找忠诚度高的和忠诚度低的客户。医药行业利用随机森林寻找和正确的成分组合来获得新药

对病人的记录进行分析确诊病情

预测股市走势，对某只股票的盈亏预期进行估计，电子商务的推荐引擎中，以确定客户对推荐的好评度，在计算机视觉中负责图像的分类，唇语识别

随机森林参数：

criterion：为了将数据生成一棵树，决策树需要找出最佳节点和最佳的分枝方法，对分类树来说，衡量这个“最佳”的指标叫做“不纯度”。通常来说，不纯度越低，决策树对训练集的拟合越好。 

random_state用来设置分枝中的随机模式的参数，默认None，在高维度时随机性会表现更明显，低维度的数据（比如鸢尾花数据集），随机性几乎不会显现。输入任意整数，会一直长出同一棵树，让模型稳定下来。splitter也是用来控制决策树中的随机选项的，有两种输入值，输入”best"，决策树在分枝时虽然随机，但是还是会优先选择更重要的特征进行分枝（重要性可以通过属性feature_importances_查看），输入“random"，决策树在分枝时会更加随机。

四个剪枝参数：max_depth, ，min_sample_leaf，min_samples_split，max_feature， min_impurity_decrease（限制信息增益的大小，信息增益小于设定数值的分枝不会发生）

决策树的参数，加8个新增参数

（1）用于调参的参数：

max_features（最大特征数）: 默认为auto。“auto”/“sqrt”（总特征个数开平方取整）,“log2”（总特征个数取对数取整）这个参数在决策树中也有其默认为None，即有多少特征用多少特征。
n_estimators：决策树个数，默认100。
（2）控制样本抽样参数：
bootstrap：每次构建树是否采用有放回样本的方式抽取数据集，默认为True。
oob_score：是否使用袋外数据来评估模型，默认为False。
boostrap和 oob_score两个参数一般要配合使用。如果boostrap是False，那么每次训练时都用整个数据集训练，如果boostrap是True，那么就会产生袋外数据。

袋外数据的概念：

有放回抽样，一些样本可能在同一个自助集中出现多次，而其他一些却可能被忽略，如果数据量足够大的时候，会有约37%的训练数据被浪费掉，没有参与建模，这些数据被称为袋外数据(out of bag data，简写为oob)。

为了这些数据不被浪费，可以把他们用来作为集成算法的测试集。也就是说，在使用随机森林时，我们可以不划分测试集和训练集，只需要用袋外数据来测试我们的模型即可。

（3）不重要参数
max_samples：构建每棵树需要抽取的最大样本数据量，默认为None
n_jobs:：设定fit和predict阶段并列执行的CPU核数,如果设置为-1表示并行执行的任务数等于计算机核数。默认为None，即采用单核计算。
verbose：控制构建数过程的冗长度，默认为0。
warm_start：当设置为True,重新使用之前的结构去拟合样例并且加入更多的估计器(estimators,在这里就是随机树)到组合器中。默认为 False

示例：

导入需要用到的包

%matplotlib inline
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_wine

导入需要的数据集:

wine = load_wine()
wine.data
wine.target

sklearn建模：

from sklearn.model_selection import train_test_split  #从sklearn中导入适当的评估器类，选择模型类
Xtrain,Xtest,Ytrain,Ytest =train_test_split(wine.data,wine.target,test_size=0.3)  #实例化
clf=DecisionTreeClassifier(random_state=0)
rfc=RandomForestClassifier(random_state=0)
clf=clf.fit(Xtrain,Ytrain)    #调用模型的fit方法对数据进行拟合
rfc=rfc.fit(Xtrain,Ytrain)
score_c=clf.score(Xtest,Ytest)   #评估模型
score_r=rfc.score(Xtest,Ytest)
print("Single Tree:{}".format(score_c)
      ,"Random Forest:{}".format(score_r))

Single Tree:0.9629629629629629 Random Forest:1.0

交叉验证效果对比：

rfc_1=[]
clf_1=[]
for i in range(10):
    rfc=RandomForestClassifier(n_estimators=25)
    rfc_s=cross_val_score(rfc,wine.data,wine.target,cv=10).mean()
    rfc_1.append(rfc_s)
    clf=DecisionTreeClassifier()
    clf_s=cross_val_score(clf,wine.data,wine.target,cv=10).mean()
    clf_1.append(clf_s)

plt.plot(range(1,11),rfc_1,label="Random Forest")
plt.plot(range(1,11),clf_1,label="Decision Tree")
plt.legend()
plt.show

superpa=[]
for i in range(200):
    rfc=RandomForestClassifier(n_estimators=i+1,n_jobs=-1)
    rfc_s=cross_val_score(rfc,wine.data,wine.target,cv=10).mean()
    superpa.append(rfc_s)
    print(max(superpa),superpa.index(max(superpa)))
    plt.figure(figsize=[20,5])
    plt.plot(range(1,201),superpa)
    plt.show()

关于调参：

大多数机器学习都有些参数需要设定，参数配置不同，模型的性能也会有显著差别，因此在进行模型评估和选择时，还需要对算法参数进行设定，这就是参数调节，简称调参。

调参的目标是提升某个模型评估指标。

以随机森林为例，我们需要提高的是模型在未知数据上的准确率（它由score，oob_score_来衡量）。在机器学习中，用来衡量模型在未知数据上的准确率的指标，叫做泛化误差。

泛化误差越小模型越好。 

一般树调参的目标都是为了降低模型的复杂度。

随机森林的调参顺序，随机森林的调参顺序一般遵循先重要后次要的原则，即先确定需要多少棵树参与建模，再对每棵树做细致的调参

eg：

调参过程

（1）n_estimators一般来说，树的棵数越多，模型效果表现越好，但树的棵数达到一定的数量之后，模型精确度不再上升，训练这个模型的计算量却逐渐变大。这个时候，再加树的数量就没必要了。

# 调参，绘制学习曲线来调参n_estimators（对随机森林影响最大）
score_lt = []

# 每隔10步建立一个随机森林，获得不同n_estimators的得分
for i in range(0,200,10):
    rfc = RandomForestClassifier(n_estimators=i+1
                                ,random_state=90)
    score = cross_val_score(rfc, data.data, data.target, cv=10).mean()
    score_lt.append(score)
score_max = max(score_lt)
print('最大得分：{}'.format(score_max),
      '子树数量为：{}'.format(score_lt.index(score_max)*10+1))
# 绘制学习曲线
x = np.arange(1,201,10)
plt.subplot(111)
plt.plot(x, score_lt, 'r-')
plt.show()

# 在71附近缩小n_estimators的范围为60-79
score_lt = []
for i in range(60,80):
    rfc = RandomForestClassifier(n_estimators=i
                                ,random_state=90)
    score = cross_val_score(rfc, data.data, data.target, cv=10).mean()
    score_lt.append(score)
score_max = max(score_lt)
print('最大得分：{}'.format(score_max),
      '子树数量为：{}'.format(score_lt.index(score_max)+60))

# 绘制学习曲线
x = np.arange(60,80)
plt.subplot(111)
plt.plot(x, score_lt,'o-')
plt.show()

(2)max_depth

# 建立n_estimators为73的随机森林
rfc = RandomForestClassifier(n_estimators=73, random_state=90)

# 用网格搜索调整max_depth
param_grid = {'max_depth':np.arange(1,20)}
GS = GridSearchCV(rfc, param_grid, cv=10)
GS.fit(data.data, data.target)

best_param = GS.best_params_
best_score = GS.best_score_
print(best_param, best_score)

sklearn的网格搜索：可为特定机器学习算法找到每一个超参数指定范围内的最佳值。也可以帮我们找到随机森林的最佳参数组合。

(3)max_features

# 用网格搜索调整max_features
param_grid = {'max_features':np.arange(5,31)}

rfc = RandomForestClassifier(n_estimators=45
                            ,random_state=90
                            ,max_depth=11)
GS = GridSearchCV(rfc, param_grid, cv=10)
GS.fit(data.data, data.target)
best_param = GS.best_params_
best_score = GS.best_score_
print(best_param, best_score)     

总结一下在sklearn中调参的思路：

① 基于泛化误差与模型复杂度的关系来进行调参；

② 根据对模型的影响程度，由大到小对参数排序，并确定哪些参数会使模型复杂度减小，哪些会增大；

③ 依次选择合适的参数，通过绘制学习曲线或网格搜索的方法调参，直到找到最大准确得分。

调参过程充满了不确定性，以上仅仅是提供一个可以参考的思路。