机器学习（1）

借这次Datawhale组队学习吃瓜教程的学习，来系统看一看西瓜书。
对于机器学习其实之前只能说是很粗糙学过一点儿。当时没怎么了解原理，只是在B站找了一些课程（比如菜菜的sklearn）简单学了一些怎么调包。

第一章绪论

引言

机器学习，就是机器基于输入数据集中的信息来训练，确立模型，对以前没见过的数据做出有用的预测。

基本术语

术语	解释
数据集	数据的集合
样本	数据集中的一条具体记录
特征	用于描述数据的输入变量
标签	要预测的真实事物或结果，也称为目标
属性	反映事件或对象在某方面的表现或性质，属性上的取值称为属性值
属性空间	属性张成的空间，又叫样本空间或输入空间
样例	拥有了标记信息的示例
维数	每个记录包含的属性个数

• 一批西瓜数据称为一个 “数据集” (data set)
• 对一个西瓜的描述是一条记录，也称为一个 “示例” (instance) 或"样本" (sample)
• “色泽” “根蒂” “敲声”，称为西瓜的属性 (attribute) 或 “特征”(feature)
• “青绿” “乌黑”，是属性上的取值，称为属性值 (attribute value)
• “色泽” “根蒂” “敲声"作为三个坐标轴，则它们张成一个用于描述西瓜的三维空间，每个西瓜都可在这个空间中找到自己的坐标位置。示例称为一个 “特征向量”
• ((色泽:青绿;根蒂二蜷缩; 敲声=浊响)，好瓜)“好瓜”，称为 “标记” (label); 拥有了标记信息的示例，则称为"样例" (example).

分类

• 传统的监督学习：每一个训练数据都有对应的标签

• 无监督学习：所有训练数据都没有对应的标签（假设同一类的训练数据，在空间中的距离更近）

• 半监督学习：一部分有标签，一部分没有标签（由于标注数据是一项比较繁琐的任务，所以通常会采用少量的标注数据、大量的未标注数据）
  分类和回归是监督学习的代表，聚类是无监督学习的代表

• 分类：标签是离散的值

• 回归：标签是连续的值

假设空间

好瓜的影响因素：色泽、根蒂、敲声，如果一个瓜的这三个属性确定下来，我们就能判断它是不是好瓜。
首先明确好瓜不仅仅是以上数据集中出现的情况，学习的目的是泛化，即通过对训练集中的瓜的学习以获得对没见过的瓜进行判断的能力。学习过程可以看作一个在所有假设组成的空间中进行搜索的过程，而搜索目标是找到与训练集匹配的假设，即能够将训练集中的瓜判断正确的假设。
所以上图，其中，色泽有青绿、乌黑、浅白3种取值，根蒂有蜷缩、稍蜷、硬挺3种取值，敲声有浊响、清脆、沉闷3种取值。
那么假设空间由形如 “(色泽=？) ∧ (根蒂=？) ∧ (敲声=？)” 的所有假设组成。
除了考虑属性色泽、根蒂、敲声的所有可能取值，还要考虑到一种属性可能无论取什么值都合适（用通配符*表示），另外有一种情况就是好瓜这个概念根本不成立（用∅表示）
假设空间规模大小的计算：
假设色泽，根蒂，敲声有3,2,2种取值。
则计算公式：（3+1）x（2+1）x（2+1）+1=37

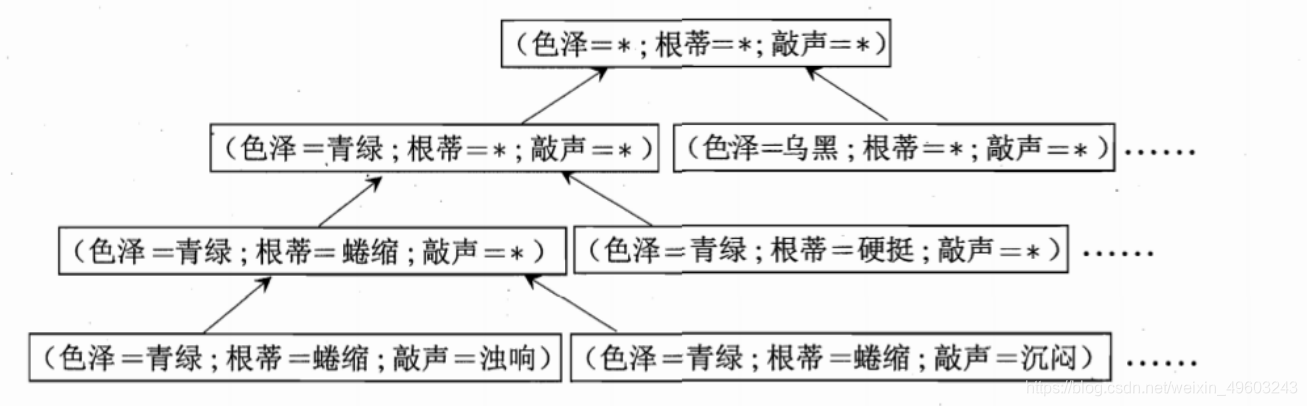
【版本空间】关键在于模型训练的方案。不同的模型方案，可以搜索到不同的假设，这个假设的集合叫做版本空间。
第二章模型评估与选择

经验误差与过拟合

术语	解释
误差	学习器预测与样本实际输出值之间的差异
训练误差	学习器在训练集上的误差
泛化误差	训练集在新样本上的误差
过拟合	学习器把训练样本自身的特点当作了所有样本潜在的样本都会具有的一般特质
欠拟合	训练样本的一般性质没学好

【Q】如何减小泛化误差
希望泛化误差小的，实际只能使经验误差最小化
【Q】无法直接获得泛化误差，训练误差又由于过拟合现象存在不适合作为标准，如何进行模型评估与选择？
通过实验测试对泛化误差进行评估（使用一个测试集来测试学习器对新样本的判别能力，即测试误差作为泛化误差的近似

评估方法

• 测试样本假设：从样本真实分布独立同分布采样而得。

• 分层采样：保留类别比例的采样方式，来保持样本类别比例类似的划分手段。

• 单次留出法往往不够稳定可靠，需要多次随机划分、重复进行实验评估后取平均值作为结果。一般而言，测试集最少包含30个样例

• 留一法缺点补充：由于“没有免费午餐”，留一法不会永远比其他评估方法准确。留一法无法应用于较大的数据集

• 留出法和、k折交叉验证法缺点：因为训练集比D的规模小，引入了因训练集规模变动而导致的估计偏差。

• 自助法的优缺点：优点：自助法适用于数据集较小的情况；自助法从原始数据集产生多个训练集，很有利于集成学习。缺点：自助法改变了原始数据分布，引入估计偏差。

术语	解释
均方误差	回归任务常用。均等代价假设。计算欧几里得距离作为代价函数。
真正例TP	预测为正例且真实为正例的
假正例FP	预测为正例但真实为反例的
真反例TN	预测为反例且真实为反例的
假反例FN	预测为反例但真实为正例的。机器学习模型的假正例和假反例越少越好。
查准率	记号为P，是真正例在所有预测为正例（真正例+假正例）中的比率。
查全率	记号为R，是真正例在所有真实为正例（真正例+假反例）中的比率。
P-R曲线	用来衡量模型的性能。学习器的P-R曲线下围成面积越大，学习器性能越好。
平衡点	它是一种度量。值大小是当“P=R”时的取值。对于两个学习器，若各自P-R曲线围城面积相同，则平衡点较大的性能更优。
Fβ度量	Fβ是基于查全率和查准率的加权调和平均，1/Fβ = (1/P + 1/R) / (1 + β^2) = (1 + β^2)PR / (β^2*P + R)。适用于类别不均衡问题，能够反映对查全率R和查准率P的不同偏好。β=1时，退化为F1度量；β>1时，更重视查全率；β<1时，更注重查准率。
宏查全率、宏查准率、宏F1	对于n个二分类混淆矩阵考察查全率和查准率，先分别求出n个查全率、查准率、F1，然后分别对n个查全率、查准率、F1求平均得到宏查全率、宏查准率、宏F1。
微查全率、微查准率、微F1	对于n个二分类混淆矩阵考察查全率和查准率，先分别求出n对真正例、假正例、真反例、假反例的平均值，然后根据平均值求查全率、查准率、F1得到微查全率、微查准率、微F1。
ROC曲线和AUC	全称“受试者工作特征”曲线，反映测试集总体期望代价（均等代价假设）。将模型对测试集N个样本的预测排序，分别以前n个样本为正例，后（N-n）个样本为反例，假正例率FPR为横轴，真正例率TPR为纵轴，n遍历从1到N，将对应假正例率FPR和真正例率TPR标在坐标系内，连成线。最理想的模型是所有正例都排在反例之前，反映在ROC曲线上就是曲线在纵轴起始点是(0, 1)。使用ROC曲线来对比不同学习器性能就是ROC曲线下面积越大（即AUC）的学习器性能越好。AUC是ROC曲线下的面积，表征任取一对正例和反例时正例预测值大于反例的概率。
真正例率TPR	真正例在真实正例中的比例，等同于查全率，越大越好。TPR不关心错判为正的样例。
假正例率FPR	假正例在真实正例中的比例。越小越好。
非均等代价	对不同类型错误赋予不同权重损失所计算出来的代价。
代价敏感错误率	不同错误类型个数乘以对应代价，求总和后除以总样本数m。综合表现了分类器性能以及度量的偏好。
正概率代价	记p为样例为正的概率，则正概率代价P+cost等于正例概率p与假反代价的积除以代价总和（假正代价+假反代价）。以正例概率p作为自变量，是分类阈值变动的量化。考虑假正代价和假反代价的比值，与具体值无关。
归一化代价	见书上公式2.25。
代价曲线	以正概率代价做横轴，归一化代价为纵轴。以样例为正概率p为自变量，取ROC曲线上每一点计算FPR和FNR（FNR=1-TPR）绘制线段，所有线段的公共下界就是代价曲线，所围成的面积就是总体期望代价。总体期望代价反映了学习器在所有条件下的总代期望，越小分类性能越好。当p=0时，假正率为0，代价总体期望最小为0，不关心假反率，因为没正例。当p=1时，总体期望代价最小为0，不关心假正率，因为没有反例。