分享啊哈算法之Dijkstra算法邻接矩阵+解决12届B组蓝桥路径问题

DijKstra算法通过边实现松弛----单源最短路径
如求下图中的1号顶点到2，3，4，5，6号顶点的最短路径

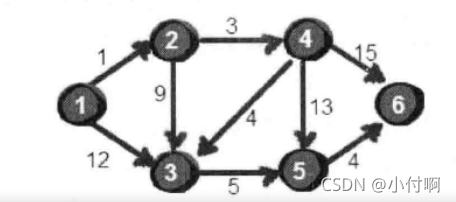
这里使用二维数组e来存储顶点之间边的关系初始值如下

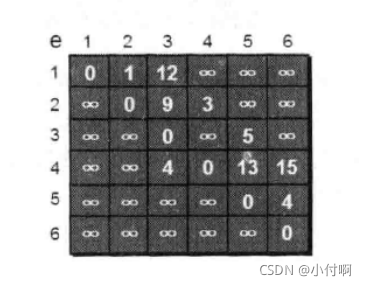
我们还需要用一个一维数组dis来存储1号顶点到其他各顶点的初始路程如下：

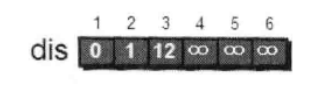
我们将此时 dis 数组中的值称为最短路程的“估计值”。
既然是求1号顶点到其余各个顶点的最短路程,那就先找一个离1号顶点最近的顶点。通过数组 dis 可知当前离1号顶点最近的是2号顶点。当选择了2号项点后, dis [2]的值就已经从“估计值”变为了“确定值”,即1号顶点到2号顶点的最短路程就是当前 dis [2]值。为什么呢?

你想啊,目前离1号项点最近的是2号顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得1号顶点到2号顶点的路程进一步缩短了。因为1号顶点到其他顶点的路程肯定没有1号到2号顶点短,对吧 O ( n _ n )0~

既然选了2号顶点,接下来再来看2号顶点有哪些出边呢。有2→3和2→4这两条边。先讨论通过2→3这条边能否让1号顶点到3号顶点的路程变短,也就是说现在来比较 dis [3]和 dis [2]+ e [2][3]的大小。其中 dis [3]表示1号项点到3号顶点的路程; dis [2]+ e [2][3]中 dis [2]表示1号项点到2号顶点的路程, e [2][3]表示2→3这条边。所以 dis [2]+ e [2][3]就表示从1号顶点先到2号顶点,再通过2→3这条边,到达3号顶点的路程。
我们发现 dis [3]=12, dis [2]+ e [2][3]=1+9=10, dis [3]> dis [2]+ e [2][3],因此 dis [3]要更新为10。这个过程有个专业术语叫做“松弛”,1号顶点到3号顶点的路程即 dis [3],通过2→3这条边松弛成功。这便是 Dijkstra 算法的主要思想:通过“边”来松弛1号顶点到其余各个顶点的路程。
同理,通过2→4( e [2][4]),可以将 dis [4]的值从∞松弛为4( dis [4]初始为四, dis [2]+ e [2][4]-1+3=4, dis [4]> dis [2]+ e [214],因此 dis [4]要更新为4)。
刚才我们对2号顶点所有的出边进行了松弛。松弛完毕之后 dis 数组为:

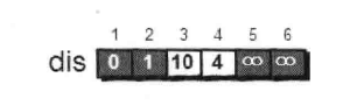
下来,继续在剩下的3、4、5和6号顶点中,选出离1号顶点最近的顶点。通过上面更新过的 dis 数组,当前离1号顶点最近的是4号顶点。此时, dis [4]的值已经从“估计值”变为了“确定值”。下面继续对4号顶点的所有出边(4→3,4→5和4→6)用刚才的方法进行松弛。松弛完毕之后 dis 数组为:

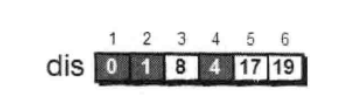
继续在剩下的3、5和6号顶点中,选出离1号顶点最近的顶点,这次选择3号顶点。此时, dis [3]的值已经从“估计值”变为了“确定值”。对3号项点的所有出边(35)进行松弛。松弛完毕之后 dis 数组为:

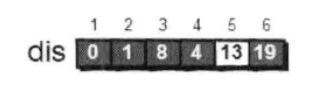
继续在剩下的5和6号顶点中,选出离1号项点最近的项点,这次选择5号顶点。此时, dis [5]的值已经从“估计值”变为了“确定值”。对5号顶点的所有出边(5→4)进行松弛。松弛完毕之后 dis 数组为:

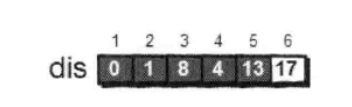
最后对6号顶点的所有出边进行松弛。因为这个例子中6号项点没有出边,因此不用处理。到此, dis 数组中所有的值都已经从“估计值”变为了“确定值”。
最终 dis 数组如下,这便是1号顶点到其余各个顶点的最短路径

OK ,现在来总结一下刚才的算法。算法的基本思想是:每次找到离源点(上面例子的源点就是1号顶点)最近的一个顶点,然后以该项点为中心进行扩展,最终得到源点到其余所有点的最短路径。基本步骤如下:

1.将所有的顶点分为两部分:已知最短路程的项点集合 P 和未知最短路径的顶点集合 Q 。最开始,已知最短路径的顶点集合 P 中只有源点一个顶点。我们这里用一个 book 数组来记录哪些点在集合 P 中。例如对于某个顶点 i ,如果 book [i]为1则表示这个顶点在集合 P 中,如果 book []i为0则表示这个项点在集合 Q 中。

2.设置源点 s 到自己的最短路径为0即 dis [ s ]=0。若存在有源点能直接到达的项点 i 则把 dis [i]设为 e [ s][i]。同时把所有其他(源点不能直接
到达的)顶点的最短路径设为 ∞

3.在集合 Q 的所有顶点中选择一个离源点。最近的顶点 u (即 dis [ u ]最小)加入到集合 P 。并考察所有以点 u 为起点的边,对每一条边进行松弛操作。例如存在一条从 u 到 v 的边,那么可以通过将边1→ v 添加到尾部来拓展一条从 s 到 v 的路径,这条路径的长度是 dis [ u ]+ e [ u] [ v] 。如果这个值比目前已知的 dis [v]的值要小,我们可以用新值来替代当前 dis [v]中的值。
重复第3步,如果集合 Q 为空,算法结束。最终 dis "数组中的值就是源点到所有顶点的最短路径。

完整的Dijkstra代码如下：

#include <bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
//0x3f3f3f3f的十进制是1061109567，是10^9级别的（和0x7fffffff一个数量级），
//而一般场合下的数据都是小于10^9的，所以它可以作为无穷大使用而不致出现数据大于无穷大的情形。
int e[100][100];
int dis[100];
int n,m;
int minm;
int book[100];
int u;
void Dijkstra(int node){
	
		book[node]=1;
		for(int i=0;i<n;i++)
			dis[i]=e[node][i];
		
	//核心 
	for(int i=0;i<n;i++){
			minm=INF;
		//来找最dis中最小的那个路径 
		for(int j=0;j<n;j++){
			if(book[j]==0 && dis[j]<minm){
				minm=dis[j];
				u=j;
			}		
		}	
			book[u]=1;
		for(int v=0;v<n;i++){
			if(e[u][v]<INF){
				if(dis[v]>dis[u]+e[u][v])
					dis[v]=dis[u]+e[u][v];
			}
		}
			
	}
	
	cout<<"顶点"<<node<<"到其他顶点的最短路径为："<<endl; 
	for(int i=0;i<n;i++){
		cout<<dis[i]<<" ";
	}
			
} 
int main(){
	cin>>n>>m;   //n为节点个数 	m边的条数 
	//初始化e
	for(int i=0;i<n;i++)
		for(int j=0;j<m;j++)
			if(i==j)
				e[i][j]=0;
			else
				e[i][j]=INF;
	
	int x,y,value;
	for(int i=0;i<m;i++){
		cin>>x>>y>>value;
		e[x][y]=value;
	} 
	Dijkstra(0);//节点0到其他节点的最短路径 
}
//6 9
//0 1 1
//0 2 12
//1 2 9
//1 3 3
//2 4 5
//3 2 4
//3 4 13
//3 5 15
//4 5 4

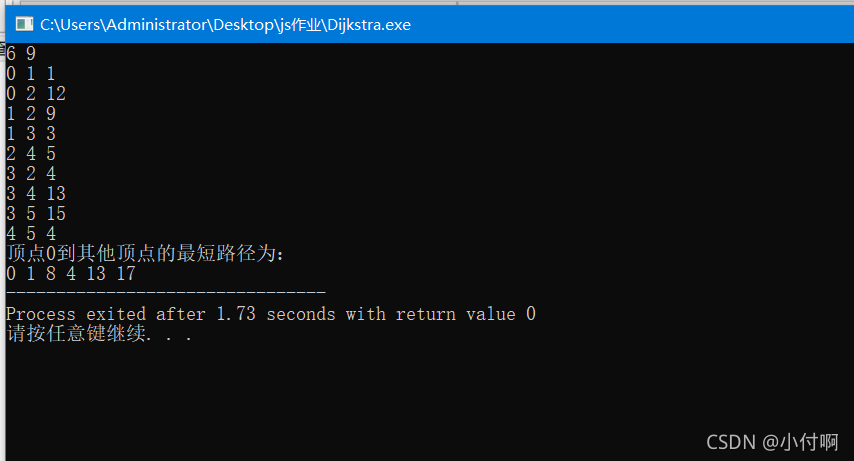
接下来，算法实战一下：
试题 E: 路径
本题总分：15 分

【问题描述】
小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图中的最短路径。
小蓝的图由 2021 个结点组成，依次编号 1 至 2021。
对于两个不同的结点 a, b，如果 a 和 b 的差的绝对值大于 21，则两个结点之间没有边相连；如果 a 和 b 的差的绝对值小于等于 21，则两个点之间有一条长度为 a 和 b 的最小公倍数的无向边相连。
例如：结点 1 和结点 23 之间没有边相连；结点 3 和结点 24 之间有一条无向边，长度为 24；结点 15 和结点 25 之间有一条无向边，长度为 75。
请计算，结点 1 和结点 2021 之间的最短路径长度是多少。
提示：建议使用计算机编程解决问题。

【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分

答案
10266837

#include <bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
int data[2022][2022];
int dis[2022];
int n=2021;
int minm;
int book[2022];
int u;
void Dijkstra(int node){
	
		book[node]=1;
		for(int i=1;i<=n;i++)
			dis[i]=data[node][i];
		
		//核心 
	for(int i=1;i<=n;i++){
		
			minm=INF;
		for(int j=1;j<=n;j++){
			if(book[j]==0 && dis[j]<minm){
				minm=dis[j];
				u=j;
			}		
		}	
			book[u]=1;
		for(int v=1;v<=n;v++){
			if(data[u][v]<INF){
				if(dis[v]>dis[u]+data[u][v])
					dis[v]=dis[u]+data[u][v];
			}
		}
			
	}
	
	cout<<"顶点"<<node<<"到2021顶点的最短路径为："<<endl; 
		cout<<dis[2021]<<" ";		
} 
int main(){
	
	for(int i=1;i<=2021;i++)
		for(int j=1;j<=2021;j++)
			if(i!=j)
				data[i][j]=INF;	
		
	
				
	for(int i=1;i<=2021;i++){
		for(int j=1;j<=2021;j++){
			if(abs(i-j)<=21 && i!=j)
				data[i][j]=(i*j)/__gcd(i,j);
		}
	}
	Dijkstra(1);
}