prim算法实现c++描述

prim算法的实现c++描述

题目描述：求下图的最小生成树
先附上答案：

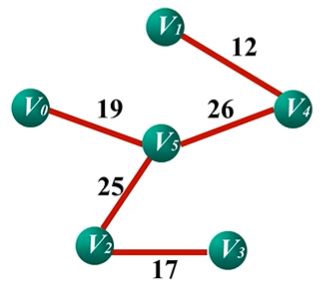
最小生成树为:U{v0,v5,v2,v3,v4,v1}

由于在算法的执行过程中，需要不断的读取任意两个顶点的权值，所以图采用邻接矩阵的存储方式比较好
U={ V0 }

V-U={V1，V2，V3，V4，V5}
shortEdge={ (V0,V1)34， (V0,V2)46，(V0,V3)∞ ，(V0,V4)∞ ，(V0,V5)19}

prim的核心思想是在集合U和剩余集合之间的所有节点，计算出它们的权值如(V0,V1)的权值为34 (V0,V3)的权值为∞ ,∞ 是因为v0和v3之间没有直达边的所以设置为无穷大

我们发现shortEdge集合里面(V0,V5)19的权值最小，然后把v5放到集和U中
U={V0 ,V5 }
V-U={V1，V2，V3，V4}
shortEdge={ (V0,V1)34，(V5,V2)25，(V5,V3)25，(V5,V4)26}
在将最小权值的节点放入到U集合里U={V0 ,V5 ，V2}.然后以此类推…最后将V-U的最后一个节点放入到集合U中就完成了最小生成树算法

数据结构的设计，设置候选最短边集shortEdge，包括adjvex[ ]和lowcost[ ] 两个域数组，分别保存候选最短边的顶点和权值…。。。。(￢_￢)好困。。。最接附代码把…

#include <bits/stdc++.h>
using namespace std;
const int MAX=10;
int vertex[MAX]; //顶点数组 
int vertexNum;//顶点数  
int arcNum;//边数 
struct matrix{
	int weight; 
}arc[MAX][MAX];//边数组--带权的矩阵 
struct path {
	int adjvex[MAX];
	int lowcost[MAX];
}shortEdge; //候选最短边集  

//数据的初始化   
void input(){ //输入格式为  节点数，边数，每个节点的值，某两个节点之间的关系和权值   如 6  9   0 1 2 3 4 5      0 1 9     这里的节点是从0开始的 
	int vi,vj,weight; //vi  vj 代表是那两个节点之间有关系(下标)    weigt是节点之间的权值 
	cin>>vertexNum;   //要设置几个节点
	cin>>arcNum;//设置几条边 
	for(int i=0;i<vertexNum;i++){  //对每个节点赋值 
		cin>>vertex[i];
	}
	for(int i=0;i<vertexNum;i++){  //边的关系数组初始化9999 表示无穷大---节点之间没有关系 
		for(int j=0;j<vertexNum;j++){
			arc[i][j].weight=9999;
		}
	} 
	for(int i=0;i<arcNum;i++){  
		cin>>vi>>vj>>weight;          
		arc[vi][vj].weight=weight;
		arc[vj][vi].weight=weight;
	}
} 
//用来寻找 shortEdge里最小权值的节点的下标 
int minEdge(path Se ,int num){
	int k=0;
	for(int i=0;i<num;i++){
		if(Se.lowcost[i]!=0 && Se.lowcost[i]!=9999){
			k=i;
			break;
		}
	}
	for(int i=0;i<num;i++){
		if(Se.lowcost[i]!=0 && Se.lowcost[i]<Se.lowcost[k]){
			k=i;
		}
	}
	return k;
}
void outputMST(int k,path putSe){  //输出最小生成树的路径 
	cout<<"("<<putSe.adjvex[k]<<","<<k<<")"<<putSe.lowcost[k]<<"   ";
} 
void Graph(int start){
	int k;//最短边的下标 
	for(int i=0;i<vertexNum;i++){  //对shortEdge辅助数组初始化 
		shortEdge.adjvex[i]=start;
		shortEdge.lowcost[i]=arc[start][i].weight;
	}
	shortEdge.lowcost[start]=0; //将起点start放入集合U 
	
	for(int i=0;i<vertexNum-1;i++){
	k=minEdge(shortEdge,vertexNum);	//在shortEdege数组里寻找最小权值的节点的下标 
	outputMST(k,shortEdge);	//输出最小权值的节点 
	shortEdge.lowcost[k]=0;   //将顶点K加入到集合U中   	U是最小路径关系的集合           V是全部的节点关系的集合 
	for(int j=0;j<vertexNum;j++){ //对shortEdge数组进行更新 
		if(arc[k][j].weight<shortEdge.lowcost[j]){
			shortEdge.adjvex[j]=k;
			shortEdge.lowcost[j]=arc[k][j].weight;
			}
		}
	} 
}
int main(){
	input();
	Graph(0);
	return 0;
}