《啊哈，算法》-13-单源最短路径问题-C语言编程实现-Dijkstra算法

一、问题描述

求一个顶点到其余各个顶点的最短路径，也叫单源最短路径。如下图，求1号顶点到2,3，4,5，6号顶点的最短路径。

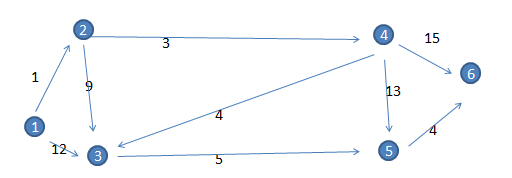
二、思路解析

1.使用二维数组e来存储顶点之间的关系。
初始值如下：

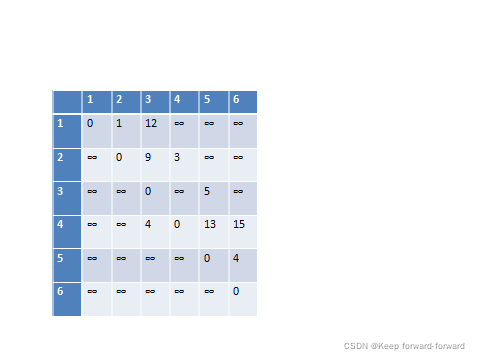
2.使用一个1维数组dist来存储1号到其余各个顶点的原始路程。如下：

3.算法的基本思想：
每次找到离源点最近的一个顶点，然后以该顶点为中心进行扩展，最终得到源点到其余所有点的最短路径。

4.算法基本步骤：
（1）将所有的顶点分为两部分：已知最短路程的顶点集合P和未知最短路径的顶点集合Q。
最开始，已知最短路径的顶点集合p只有源点一个点点。这里 我们用book数组来记录哪些顶点在集合P中，如果book[i]为0则表示这个顶点在集合Q中。
（2）设置源点s到自己的最短路径为0，即dis[s]=0.
若存在有源点可以直接到达的顶点i,则把dis[i]设为e[s][i].
同时把所有其他源点不能直接到达的顶点的最短路径设置为∞。
（3）在集合Q的所有顶点中选择一个离源点s最近的顶点u(即dis[u]最小）加入到集合P。
并考察所有以点u为起点的边，对每一条边镜像松弛操作。
例如存在1条从u到v的边，那么可以通过将边u->v添加到尾部扩展一条从s到v的路径，这条路径的长度是dis[u]+e[u][v].
如果这个值比目前已知的dis[v]的值要小，我们可以用新值来替代当前dis[v]中的值。
（4）重复第3步，如果集合Q为空，算法结束。最终dis数组中的值就是源点到所有顶点的最短路径。

三、代码复现

#include<stdio.h>
int main(){
	int e[10][10],dis[10],book[10],i,j,n,m,t1,t2,t3,u,v,min;
	int inf=99999999;//存储一个我们认为的正无穷值
	//读入n和m,n表示顶点数目，m表示边的数目
	scanf("%d %d",&n,&m);
	
	//初始化
	for(i=1;i<=n;i++)
		for(j=1;j<=n;j++)
			if(i==j) e[i][j]=0;
			else e[i][j]=inf;
			
	//读入边
	for(i=1;i<=m;i++)
	{
		scanf("%d %d %d",&t1,&t2,&t3);
		e[t1][t2]=t3;
	} 
	
	//初始化dist数组
	for(i=1;i<=n;i++)
	{
		//这里是1号顶点到其余各个顶点的初始路程 
		dis[i]=e[1][i];
	} 
	
	//book数组初始化
	for(i=1;i<=n;i++)
		book[i]=0;
	book[1]=1; 
	
		 
	//Dijkstra算法的核心代码 
	for(i=1;i<=n-1;i++){
		//找到离1号最近的顶点
		min=inf;
		for(j=1;j<=n;j++){ 
			if(book[j]==0 &&dis[j]<min){
				min=dis[j];
				u=j;
			}
		}
		book[u]=1;
		for(v=1;v<=n;v++){
			if(e[u][v]<inf){
				if(dis[v]>dis[u]+e[u][v])
					dis[v]=dis[u]+e[u][v];
			}
		} 
	}
		
					
   //输出最终结果
   for(i=1;i<=n;i++)
   		printf("%d ",dis[i]);
	
	getchar();
	getchar();
	return 0;
} 

四、总结

该算法的时间复杂度是O（N的平方）。
下一章节可以用“堆”来优化，降低时间复杂度。
也可以对于比较稀疏的图，使用邻接表来代替邻接矩阵，降低时间复杂度。
该算法是一个基于贪心策略的算法，算法每扩展一个路程最短的点，更新与其相邻的点的路程。
根据算法原理，用这个算法求最短路径是不能有负权边的。