神经网络-数模应用

人工神经元模型/人工神经网络(artificial neural network,NN),有三个基本要素
（i）一组连接（对应于生物神经元的突触），连接强度由各连接上的权值表示，权值为正表示激活，为负表示抑制。
（ii）一个求和单元，用于求取各输入信号的加权和（线性组合）。
（iii）一个非线性激活函数，起非线性映射作用并将神经元输出幅度限制在一定范围内（一般限制在(0,1) 或(−1,1) 之间）。
此外还有一个阈值${\theta }_k$ （或偏置$b_k=-{\theta }_k$ ）。

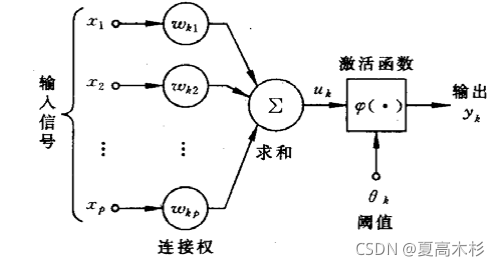
以上作用可分别以数学式表达出来：

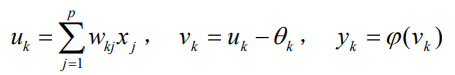
• 神经网络应用
  • 模式分类：需要提供已知样本
  • 聚类：不需要提供已知样本
  • 回归与拟合：相似的样本输入在神经网络的映射下，往往能得到相近的输出
  • 优化计算：寻找一组参数组合，由该组合确定的目标函数达到最小值
  • 数据压缩：将数据保存于连接权值中
• 神经网络种类
  • 单层感知器
  • 线性网络
  • BP网络
  • 径向基网络
  • 自组织网络
  • 反馈网络
  • 随机神经网络
• 按性能分：连续型和离散型网络，或确定型和随机型网络
• 按拓扑结构分：前向网络和反馈网络
• 按学习方法分：监督学习网络和无监督学习网络
• 按连接突触性质分：一阶线性关联网络和高阶线性非关联网络

遗传算法优化BP神经网络-非线性函数拟合

BP(误差反向传播算法) 神经网络是包含多个隐含层的网络，具备处理线性不可分问题的能力，是一种多层前向网络(核心)，又叫多层感知器
广泛应用于分类识别、逼近、回归、压缩等领域。
BP是一种按误差反向传播算法训练的多层前馈网络，它能学习和存储大量的输入-输出模式映射关系，而无需事前描述这种映射关系的数学模型。它的学习规划是使用最速下降法，通过误差反向传播来不断跳转网络的权值和阈值，使网络的误差平方和最小。

• 感知器：单层前向网络。除了输入层和输出层只有一层神经元节点。(只用来解决线性可分的二分类问题)
• 隐含层：除了输入层和输出层以外的其他各层
• 误差反向传播：误差信号反向传播。修正权值时，网络根据误差从后往前逐层进行修正
• 反馈神经网络：输出层的
• 传递函数
  • 必须处处可导
  • 一般使用s型函数(Sigmoid函数)
  • 最大可能保留数据特征，容错性高
    

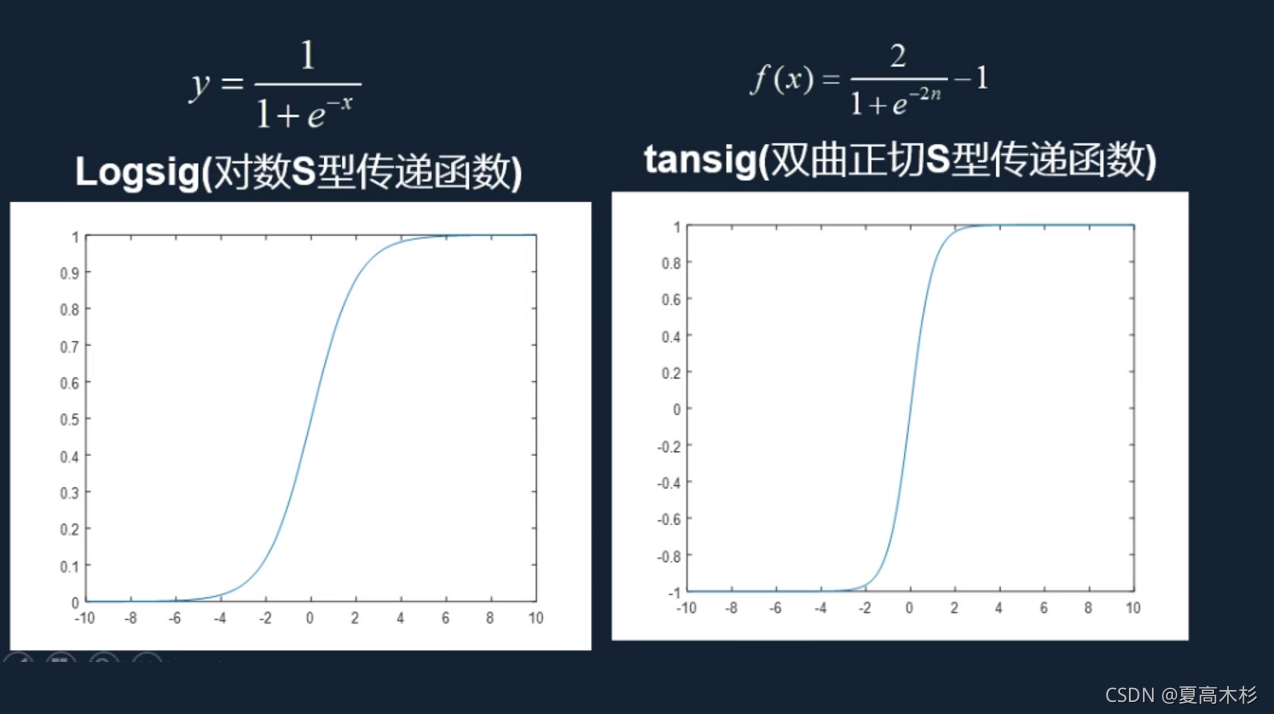
BP是一种按误差反向传播算法(Back-Propagation Algorithm)训练的多层前馈网络，它能学习和存储大量的输入-输出模式映射关系，而无需事前描述这种映射关系的数学模型。它的学习规划是使用最速下降法，通过误差反向传播来不断跳转网络的权值和阈值，使网络的误差平方和最小。

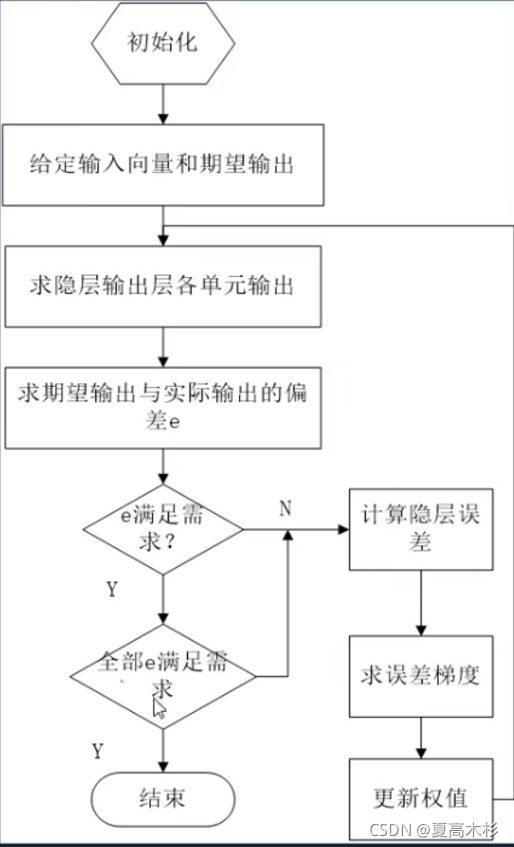
遗传算法优化BP神经网络分为BP神经网络结构确定、遗传算法优化和BP神经网络预测3个部分。

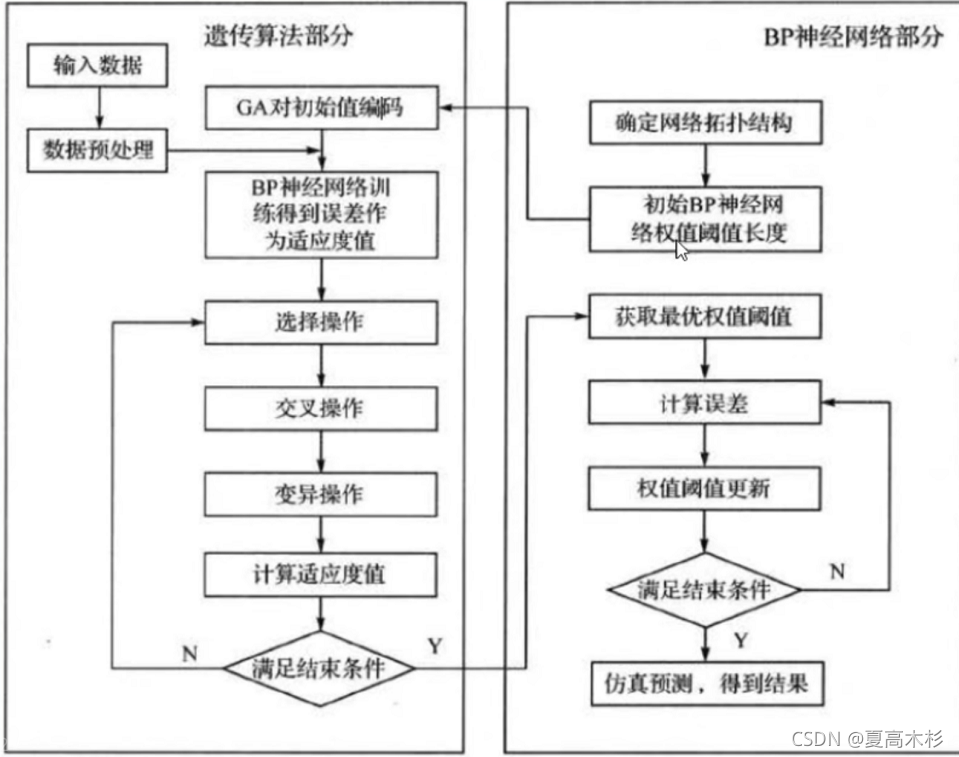
• 神经网络结构确定部分根据拟合函数，输入输出参数个数确定BP神经网络结构，进而确定遗传算法个体长度。
• 遗传算法优化神经网络的权值和阈值，个体通过适应函数计算个体适应度值。遗传算法通过选择、交叉和变异操作找到最优适应度值对应个体
• BP神经网络预测用遗传算法得到最优个体对网络初始权值和阈值赋值，网络经训练后预测函数输出
• 拟合函数中输入层节点m，输出层节点n，a为1~10之间的调节常数 h为隐含层节点数目
• $h=\sqrt{m+n}+a$
• 隐函数条件：
  • 节点数必须小于N-1，(N为训练样本数)，否则网络模型的系统误差与训练样本的特征无关而趋于0，即建立的网络模型没有泛化能力。
• 同理：输入层的节点数也必须小于N-1