神经网络学习入门（二）

继上一篇：

        关于感知机，既有好消息，也有坏消息。好消息是，即便对于复杂的函数，感知机也隐含着能够表示它的可能性。上一章已经介绍过，即便是计算机进行的复杂处理，感知机（理论上）也可以将其表示出来。坏消息是，设定权重的工作，即确定合适的、能符合预期的输入与输出的权重，现在还是由人工进行的。 神经网络的出现就是为了解决刚才的坏消息。具体地讲，神经网络的一个重要性质是它可以自动地从数据中学习到合适的权重参数。

从感知机到神经网络

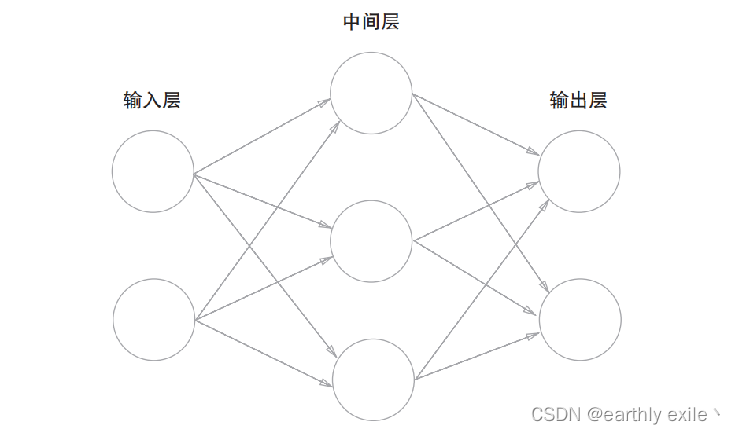
        神经网络和前面介绍的感知机有很多共同点。这里，我们主要以两者的差异为中心，来介绍神经网络的结构。 用图来表示神经网络的话，如图所示。我们把最左边的一列称为输入层，最右边的一列称为输出层，中间的一列称为中间层。中间层有时也称为隐藏层。“隐藏”一词的意思是，隐藏层的神经元（和输入层、输出层不同肉眼看不见）

我们再回顾一下上一篇讲的感知机

感知机的图像表达

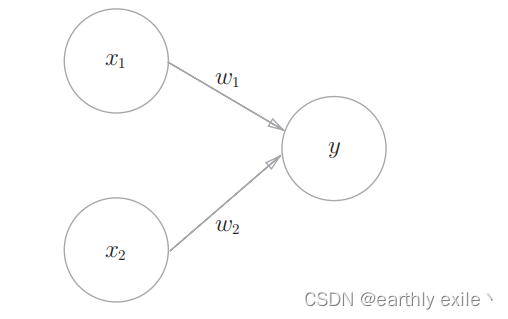
感知机接收x1和x2两个输入信号，输出y

感知机的数学表达

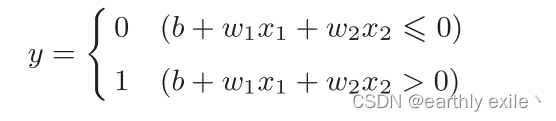
b是被称为偏置的参数，用于控制神经元被激活的容易程度；而w1和w2 是表示各个信号的权重的参数，用于控制各个信号的重要性。

我们将上述数学表达式改写一下：  y = h(b + w1x1 + w2x2) 此处

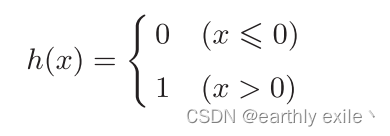
刚才登场的h（x）函数会将输入信号的总和转换为输出信号，这种函数一般称为激活函数（activation function）。如“激活”一词所示，激活函数的作用在于决定如何来激活输入信号的总和。

我们将上面的数学表达式按照下述过程从左至右再转化一下

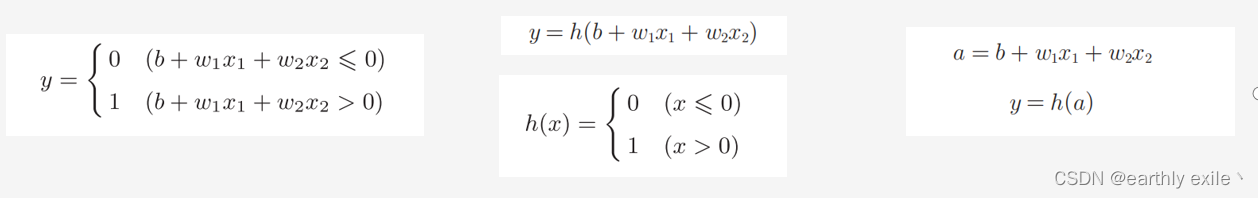
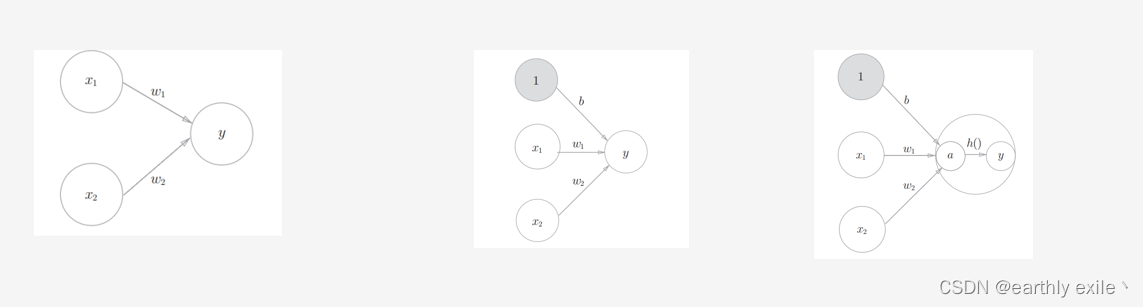
到了最右边就是完整的神经网络啦！无论是RNN(循环神经网络)，LSTM（长短期记忆网络），GAN（对抗神经网络） ，他们的共同基础都是基础神经网络。因此牢记神经网络最最基本的结构和原理非常必要。

下面我们来了解一下上述公式中常用的的h（）

常用的激活函数

阶越函数

阶越函数的数学表达式：

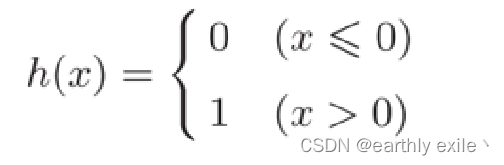
阶越函数的图像

如图3-6所示，阶跃函数以0为界，输出从0切换为1（或者从1切换为0）。

它的值呈阶梯式变化，所以称为阶跃函数。

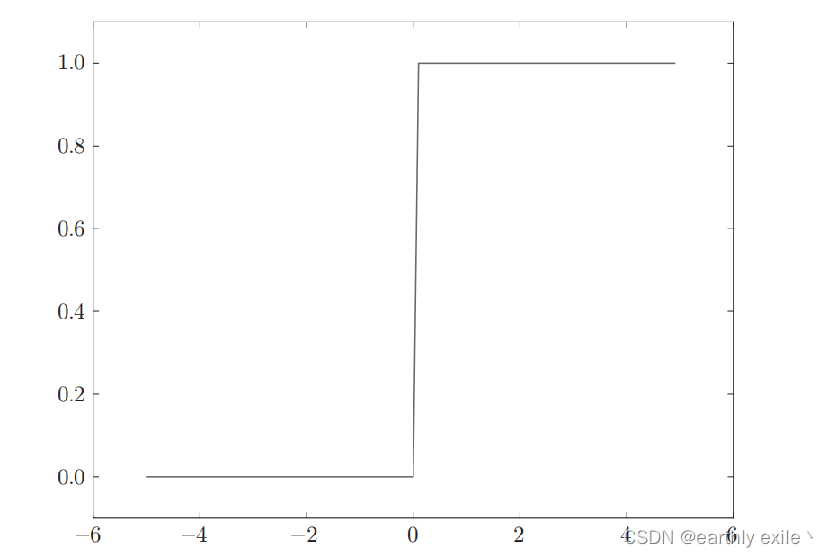
sigmoid函数

sigmoid函数的数学表达式

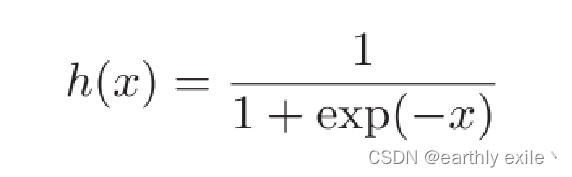
sigmoid函数的函数图像

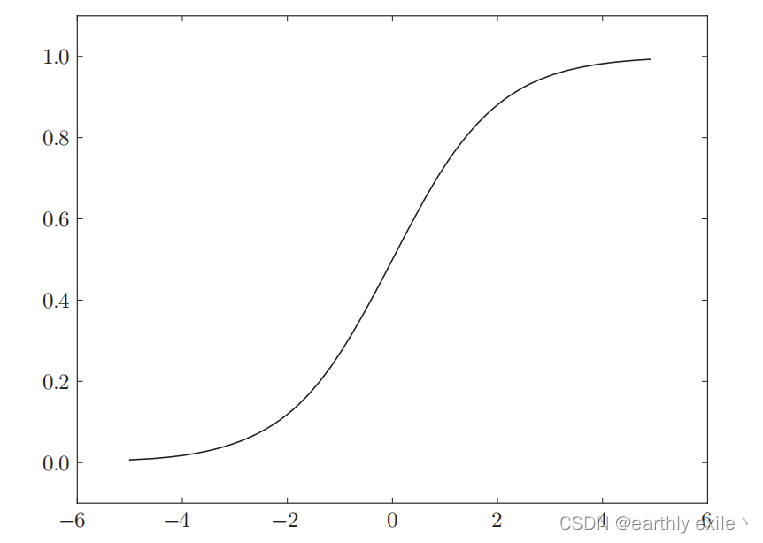
ReLU函数

ReLU函数的数学表达式

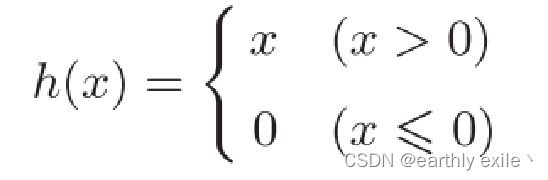
ReLU函数的数学表达式

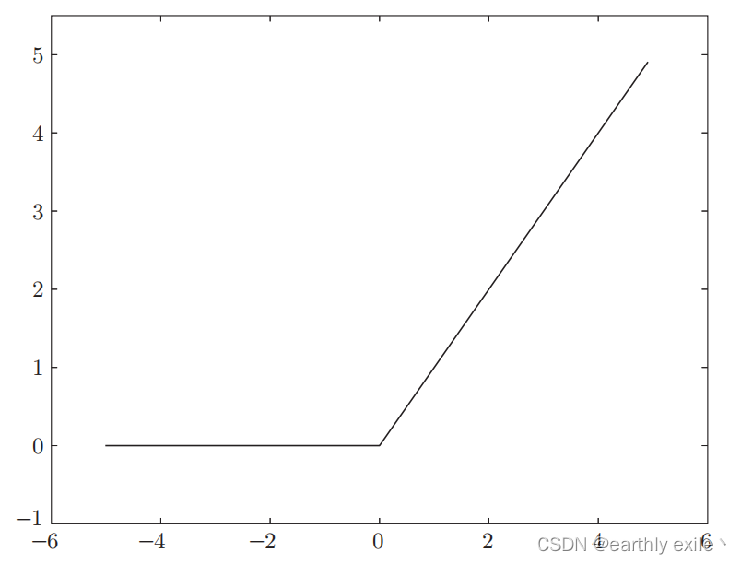
        在实际搭建神经网络的过程中我们可以根据实际需求（主要是根据任务类型-回归问还是分类）选择不同的激活函数。但是选择对于激活函数也不是全无要求

        神经网络的激活函数必须使用非线性函数。换句话说，激活函数不能使用线性函数。为什么不能使用线性函数呢？因为使用线性函数的话，加深神经网络的层数就没有意义了。线性函数的问题在于，不管如何加深层数，总是存在与之等效的“无隐藏层的神经网络”。

神经网络需要掌握的工具

        1. 编程语言 Python： Python是一个简单、易读、易记的编程语言，而且是开源的，可以免费地自由使用。Python可以用类似英语的语法编写程序，编译起来也不费力，因此我们可以很轻松地使用Python。在科学领域，特别是在机器学习、数据科学领域，Python也被大量使用。Python除了高性能之外，凭借着 NumPy、SciPy等优秀的数值计算、统计分析库，在数据科学领域占有不可动摇的地位。深度学习的框架中也有很多使用Python的场景，比如Caffe、TensorFlow、Chainer、Theano等著名的深度学习框架都提供了Python接口。

        2. NumPy：一个用python实现的科学计算，包括：1、一个强大的N维数组对象Array；2、比较成熟的（广播）函数库；3、用于整合C/C++和Fortran代码的工具包；4、实用的线性代数、傅里叶变换和随机数生成函数。numpy和稀疏矩阵运算包scipy配合使用更加方便。numpy内置了并行运算功能，当系统有多个核心时，做某种计算时，numpy会自动做并行计算。Numpy底层使用C语言编写，数组中直接存储对象，而不是存储对象指针，所以其运算效率远高于纯Python代码。         3.Matplotlib:  是一个 Python 的 2D绘图库。方便我们观察学习效果。

        4.pytorch： 主流的开源深度学习框架，可以通过简单的配置实现神经网络模型，相较于 tensorflow 有着易用，简洁，的优点。    

        为什么使用Numpy

下面我们对一个简化神经网络推理过程进行演示，神经网络图如下

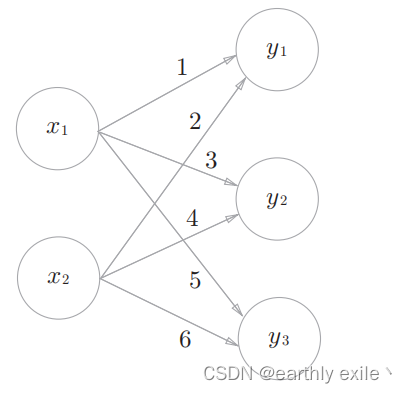
假设输入值为 X1 =1 ,X2 = 2 ,箭头上的数值为对应的权重W,下面我们通过常规的计算方法来计算y1，y2，y3的值。      

常规方法计算：

y1 = X1 * 1 + X2 * 2 =  1 * 1 + 2 * 2 = 5

y2 = X1 * 1 + X2 * 4 = 1 * 3 + 2 * 4 = 11

y3 = X1 * 5 + X2 * 6 = 1 * 5 + 2 * 6 = 17

使用Numpy计算

#输入值记作一维数组

X = np.array([1, 2]) #权重用二维数组表示

W = np.array([[1, 3, 5], [2, 4, 6]])

Y = np.dot(X, W)     #点积运算

print(Y)  ->>   [ 5 11 17]

通过观察可以发现，使用Numpy可以简单迅速的计算出矩阵乘积。

神经网络的foward计算

神经网络通过上述计算不断一层一层推进，这就是神经网络推理过程做的事，我们将这个过程称为foward计算

        

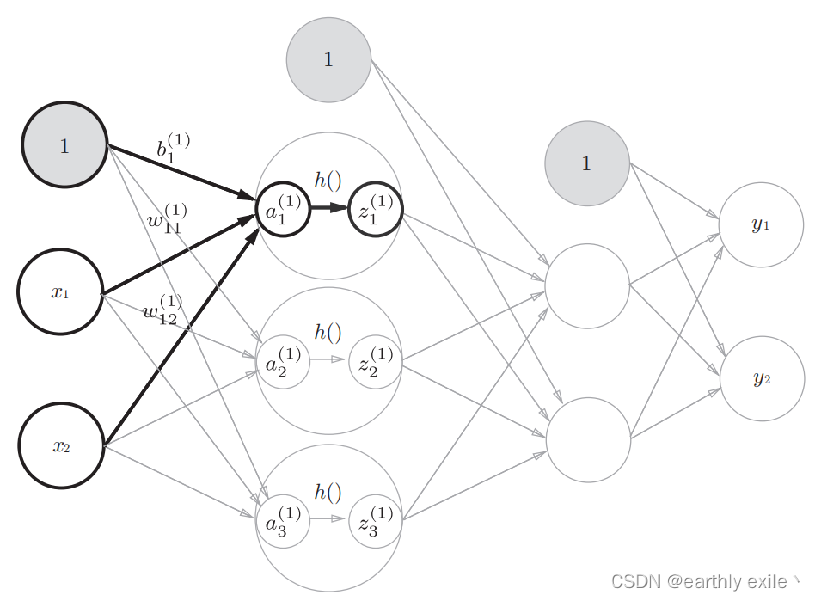
实际在神经网络中，信号通过权重计算传入下一级之后还会经过偏置 和 激活函数，就是图种的h(),此处我们用sigmoid函数作为我们的激活函数，我们只需要在上面的代码中加入简单一行代码即可：

        使用Numpy计算

#输入值记作一维数组
X = np.array([1, 2])
# 权重用二维数组表示
W = np.array([[1, 3, 5], [2, 4, 6]])
# B为偏置
B = np.array([1, 1, 1])
Y = np.dot(X, W)   # 点积运算 权重处理
A = Y + B              # 此处B为偏置
B = sigmoid(A)      # 流过激活函数
print(Y)   -> [ 5 11 17]
print(A)   -> [ 5 11 17]
print(B)   -> [0.99752738 0.99999386 0.99999998]

输出层的设计

        机器学习的问题大致可以分为分类问题和回归问题。分类问题是数据属于哪一个类别的问题。比如，区分图像中的人是男性还是女性的问题就是分类问题。而回归问题是根据某个输入预测一个（连续的）数值的问题。比如，根据一个人的图像预测这个人的体重的问题就是回归问题。

        神经网络可以用在分类问题和回归问题上，不过需要根据情况改变输出层的激活函数。一般而言，回归问题用恒等函数，分类问题用softmax函数。

恒等函数就是输入值原样输出-即不做任何操作，可省略

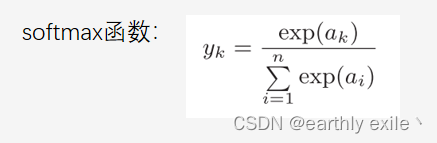
softmax函数的输出是0.0到1.0之间的实数。并softmax 函数的输出值的总和是1。输出总和为1是softmax函数的一个重要性质。正因为有了这个性质，我们才可以把softmax函数的输出解释为“概率”。

给我们的神经网络加上输出层后，就迎来了神经网络的最终形态，如下图所示：

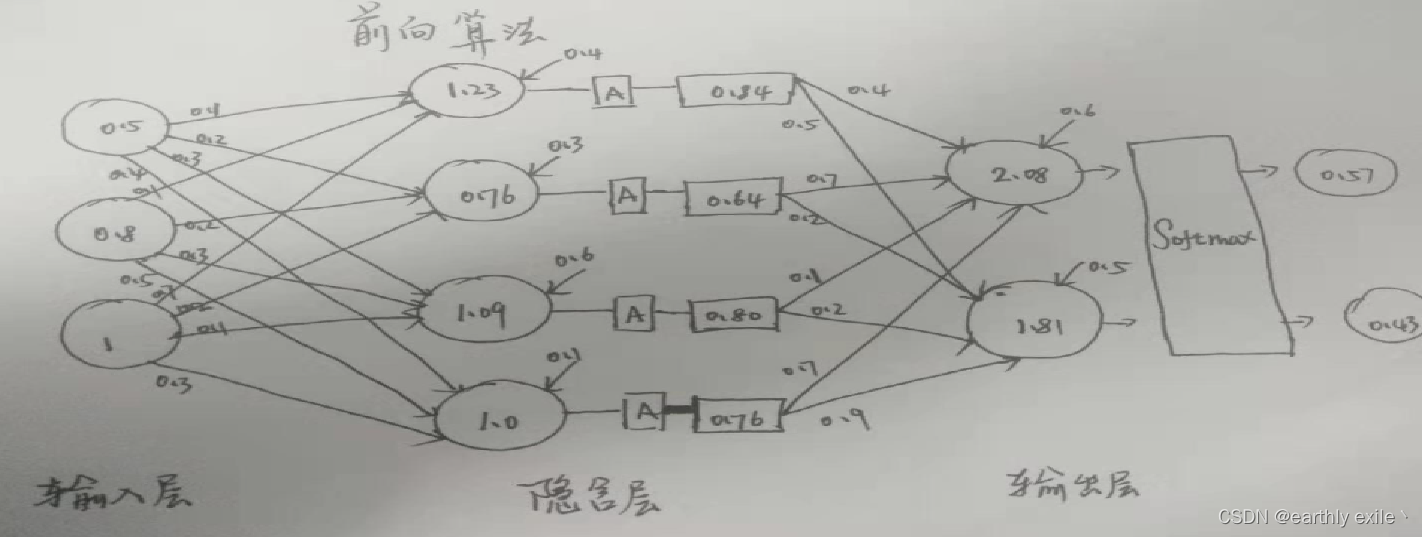
至此我们就了解了神经网络的全貌。

MNIST数据集

在手写数字识别前，先给大家介绍一下MNIST数据集

        MNIST是机器学习领域最有名的数据集之一，被应用于从简单的实验到发表的论文研究等各种场合。实际上，在阅读图像识别或机器学习的论文时，MNIST数据集经常作为实验用的数据出现。MNIST数据集是由0到9的数字图像构成的。训练图像有6万张，测试图像有1万张，这些图像可以用于学习和推理。MNIST数据集的一般使用方法是，先用训练图像进行学习，再用学习到的模型度量能在多大程度上对测试图像进行正确的分类。

        MNIST的图像数据是28像素 × 28像素的灰度图像（1通道），各个像素的取值在0到255之间。每个图像数据都相应地标有“7”“2”“1”等标签。 我们的目的是识别MNIST数据集的图片，而MINST数据集的一张图片可以用一个784的一维数组表示，输入层的784这个数字来源于图像大小的28 × 28 = 784，输出层的10这个数字来源于10类别分类（数字0到9，共10类别）。此外，这个神经网络有2个隐藏层，第1个隐藏层有50个神经元，第2个隐藏层有100个神经元。这个50和100可以设置为任何值。 首先我们将MNIST数据集下载下来，我们通过mnist_show.py 脚本来查看一下MNIST图集(这一步就是简单的图像读取和展示，如果读者可以直接复制下来运行，不用深究)，

脚本源码如下：

# coding: utf-8
try:
    import urllib.request
except ImportError:
    raise ImportError('You should use Python 3.x')
import os.path
import gzip
import pickle
import os
import numpy as np


url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
    'train_img':'train-images-idx3-ubyte.gz',
    'train_label':'train-labels-idx1-ubyte.gz',
    'test_img':'t10k-images-idx3-ubyte.gz',
    'test_label':'t10k-labels-idx1-ubyte.gz'
}

dataset_dir = os.path.dirname(os.path.abspath(__file__))
save_file = dataset_dir + "/mnist.pkl"

train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784


def _download(file_name):
    file_path = dataset_dir + "/" + file_name
    
    if os.path.exists(file_path):
        return

    print("Downloading " + file_name + " ... ")
    urllib.request.urlretrieve(url_base + file_name, file_path)
    print("Done")
    
def download_mnist():
    for v in key_file.values():
       _download(v)
        
def _load_label(file_name):
    file_path = dataset_dir + "/" + file_name
    
    print("Converting " + file_name + " to NumPy Array ...")
    with gzip.open(file_path, 'rb') as f:
            labels = np.frombuffer(f.read(), np.uint8, offset=8)
    print("Done")
    
    return labels

def _load_img(file_name):
    file_path = dataset_dir + "/" + file_name
    
    print("Converting " + file_name + " to NumPy Array ...")    
    with gzip.open(file_path, 'rb') as f:
            data = np.frombuffer(f.read(), np.uint8, offset=16)
    data = data.reshape(-1, img_size)
    print("Done")
    
    return data
    
def _convert_numpy():
    dataset = {}
    dataset['train_img'] =  _load_img(key_file['train_img'])
    dataset['train_label'] = _load_label(key_file['train_label'])    
    dataset['test_img'] = _load_img(key_file['test_img'])
    dataset['test_label'] = _load_label(key_file['test_label'])
    
    return dataset

def init_mnist():
    download_mnist()
    dataset = _convert_numpy()
    print("Creating pickle file ...")
    with open(save_file, 'wb') as f:
        pickle.dump(dataset, f, -1)
    print("Done!")

def _change_one_hot_label(X):
    T = np.zeros((X.size, 10))
    for idx, row in enumerate(T):
        row[X[idx]] = 1
        
    return T
    

def load_mnist(normalize=True, flatten=True, one_hot_label=False):
    """读入MNIST数据集
    
    Parameters
    ----------
    normalize : 将图像的像素值正规化为0.0~1.0
    one_hot_label : 
        one_hot_label为True的情况下，标签作为one-hot数组返回
        one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
    flatten : 是否将图像展开为一维数组
    
    Returns
    -------
    (训练图像, 训练标签), (测试图像, 测试标签)
    """
    if not os.path.exists(save_file):
        init_mnist()
        
    with open(save_file, 'rb') as f:
        dataset = pickle.load(f)
    
    if normalize:
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].astype(np.float32)
            dataset[key] /= 255.0
            
    if one_hot_label:
        dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
        dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
    
    if not flatten:
         for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].reshape(-1, 1, 28, 28)

    return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label']) 


if __name__ == '__main__':
    init_mnist()

# coding: utf-8
import sys, os

sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image


# 将 28*28的二维数组以图片的方式展示
def img_show(img_array):
    pil_img = Image.fromarray(np.uint8(img_array))
    pil_img.show()


# 加载MNIST数据集 (训练图像 ,训练标签 )，(测试图像，测试标签 )
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
# 图片index
index = 5
# 取出训练数据集指定位置数据
img = x_train[index]
# 取出训练数据集指定位置对应的标签
label = t_train[index]
print(label)  # 5
# 格式为一个拥有784个元素的一维数组
print(img.shape)  # (784,)
# 把图像的形状变为原来的尺寸，转换成 28 * 28的二维数组
img = img.reshape(28, 28)
# 查看转换之后数据的格式
print(img.shape)  # (28, 28)
img_show(img)

    下面我们通过一个简单的神经网络来识别上诉MNIST的数据集中的数据

  

# coding: utf-8
import os
import pickle
import sys

import numpy as np

from common.functions import sigmoid, softmax
from dataset.mnist import load_mnist
from PIL import Image

sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定


def img_show(index):
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=False, flatten=True, one_hot_label=False)
    img = x_test[index]
    img = img.reshape(28, 28)
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()


# 加载MNIST数据集 (训练图像 ,训练标签 )，(测试图像，测试标签 )
def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test


# 初始化权重，偏置 参数   这部分参数由模型训练而来，此处我们使用训练好的参数，后面会说如何来确定这些参数。
def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network


# 推断 会是 0 ~ 9 中每个数字的概率
def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    # 信号流过权重和偏置
    a1 = np.dot(x, W1) + b1
    # 流过激活函数
    z1 = sigmoid(a1)
    # 进入下一层神经网络
    # 信号流过权重和偏置
    a2 = np.dot(z1, W2) + b2
    # 流过激活函数
    z2 = sigmoid(a2)
    # 流向输出层 信号流过权重和偏置
    a3 = np.dot(z2, W3) + b3
    # 流进输出层激活函数
    y = softmax(a3)
    return y


# 获取MNIST数据集
x, t = get_data()
# 初始化权重,偏置,参数
network = init_network()
# 随机选取一张测试图片
index = 1001
# 使用神经网络来推断
y = predict(network, x[index])
print(y)
p = np.argmax(y)
print(p)

# 统计 1000张测试图片的正确识别率，推断结果与label相同则表示成功识别
accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])
    p = np.argmax(y)  # 获取概率最高的元素的索引
    if p == t[i]:
        accuracy_cnt += 1

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

# 显示一下图片
img_show(index)


#  图像人看起来是7
# 输出层神经元位置
# 0               1             2             3            4             5             6              7             8             9
# 神经网络的输出
# [8.4412488e-05 2.6350656e-06 7.1549456e-04 1.2586262e-03 1.1727954e-06 4.4990808e-05 1.6269318e-08 9.9706501e-01 9.3744702e-06 8.1831159e-04]
# 理想状态下的输出
# [0              0              0               0            0            0             0             1             0           0            ]                           ]
# 思考如何衡量上面两组数据的误差？

我们来看一下运行结果

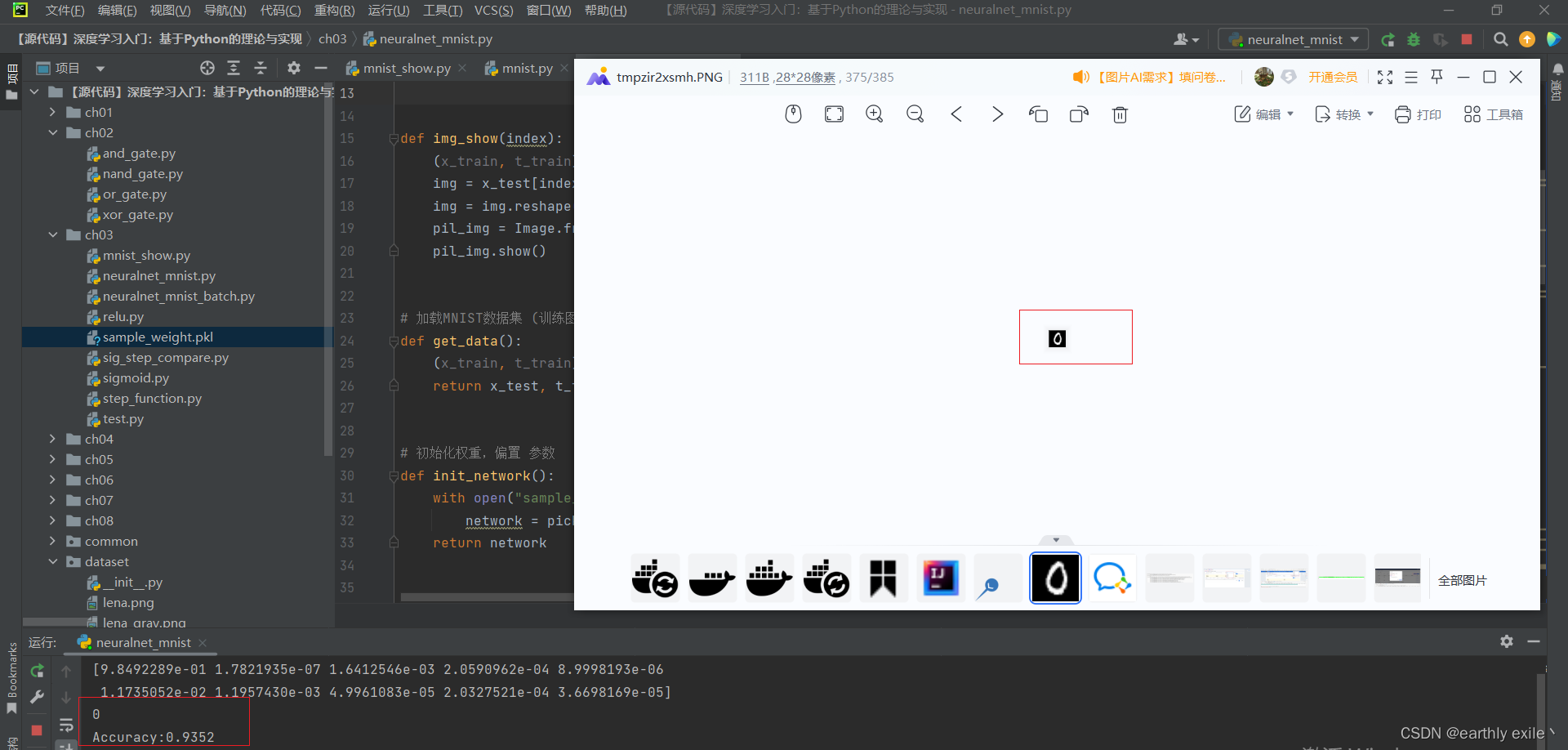
程序识别出来图像为0的概率为93.52%与我们人眼看到的没有出入。

注意上述脚本使用的是训练好的权重，我放在这里（暂时上传有点问题稍后上传）

        我们使用训练好的权重和偏置参数实现了一个识别率高达0.9352的神经网络模型，可是这些权重参数又是如何确定的呢？ 神经网络的特征就是可以从数据中学习。所谓“从数据中学习”，是指可以由数据自动决定权重参数的值。这是非常了不起的事情！因为如果所有的参数都需要人工决定的话，工作量就太大了。前面感知机的例子中，我们对照着真值表，人工设定了参数的值，但是那时的参数只有3个。而在实际的神经网络中，参数的数量成千上万，在层数更深的深度学习中，参数的数量甚至可以上亿，想要人工决定这些参数的值是不可能的。

损失函数

        在了解神经网络事如何自我学习之前先了解一下损失函数。 神经网络的学习通过某个指标表示现在的状态。然后，以这个指标为基 准，寻找最优权重参数。神经网络以某个指标为线索寻找最优权重参数。神经网络的学习中所用的指标称为损失函数（loss function）。这个损失函数可以使用任意函数，但一般用均方误差和交叉熵误差等。

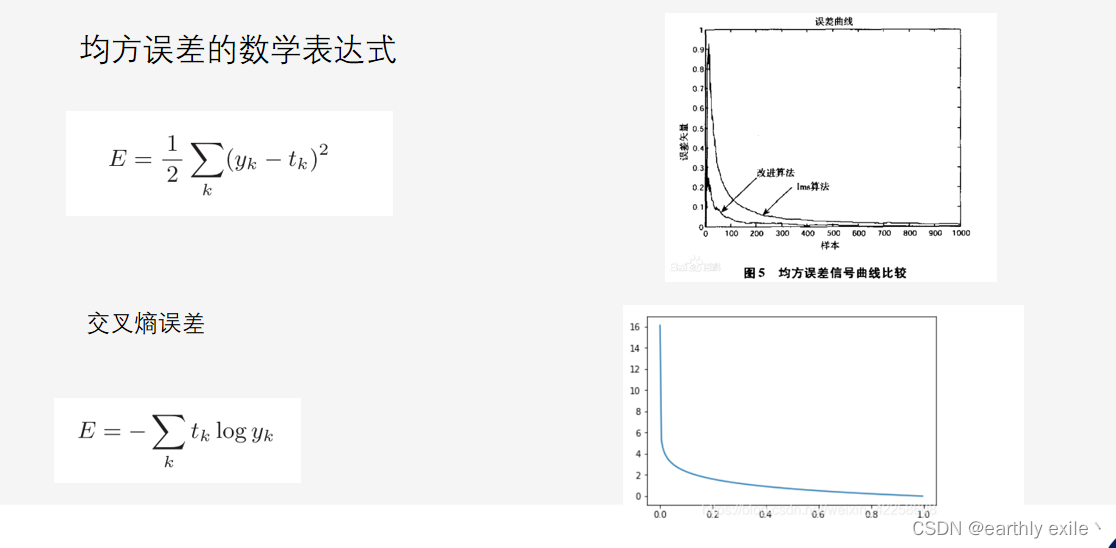
        损失函数是表示神经网络性能的“恶劣程度”的指标，即当前的神经网络对监督数据在多大程度上不拟合，在多大程度上不一致。以“性能的恶劣程度”为指标可能会使人感到不太自然，但是如果给损失函数乘上一个负值，就可以解释为“在多大程度上不坏”，即“性能有多好”。并且，“使性能的恶劣程度达到最小”和“使性能的优良程度达到最大”是等价的，不管是用“恶劣程度”还是“优良程度”，做的事情本质上都是一样的。

        结论，神经网络的推断结果通过损失函数计算之后的损失值越小，则表示神经网络的性能越好。通过损失函数值的变化我们可以定量的来衡量神经网络性能。

        损失函数是表示神经网络性能的“恶劣程度”的指标，即当前的神经网络对监督数据在多大程度上不拟合，在多大程度上不一致。以“性能的恶劣程度”为指标可能会使人感到不太自然，但是如果给损失函数乘上一个负值，就可以解释为“在多大程度上不坏”，即“性能有多好”。并且，“使性能的恶劣程度达到最小”和“使性能的优良程度达到最大”是等价的，不管是用“恶劣程度”还是“优良程度”，做的事情本质上都是一样的。

导数与微分

导数就是表示某个瞬间的变化量

导数的数学表达式

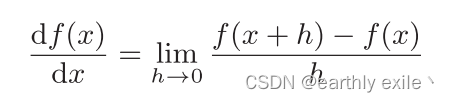
导数体现在函数图像上为某一点的切线斜率

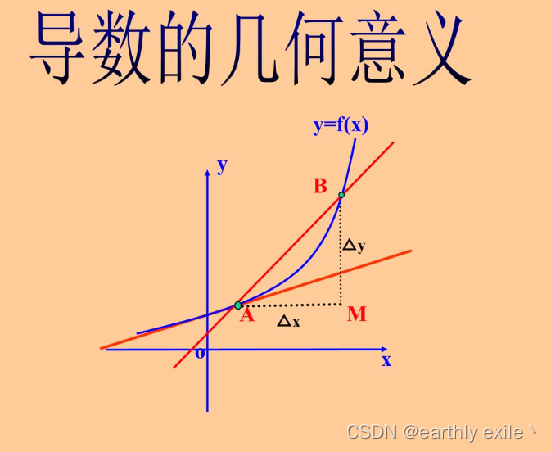
如何计算导数？

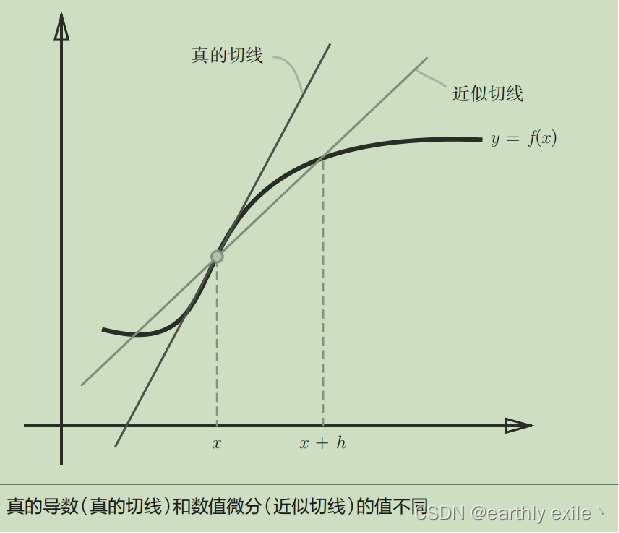
导数的计算，一般有两种方法，数值数值求导和解析求导。

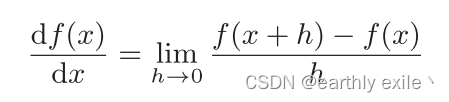
数值求导和解析求导的图像表达

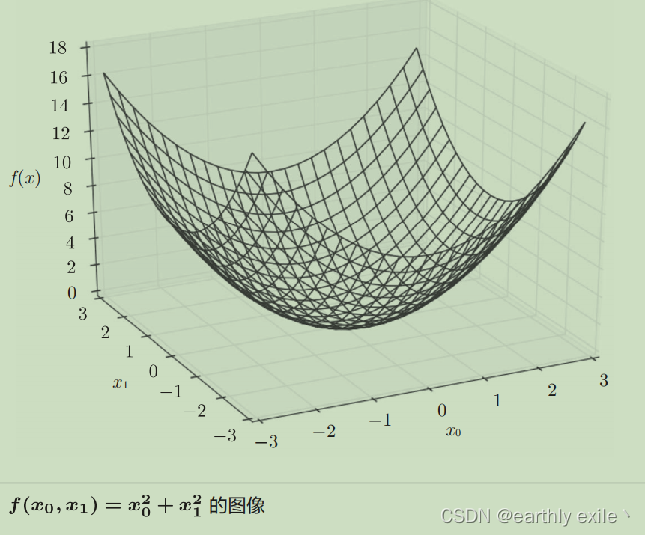
三维空间的导数

三维空间的导数由两个向量组成，那么如何计算三维空间具体某个点的导数？

计算多维空间导数的步骤。

        

在刚才的例子中，我们按变量分别计算了x0和x1的偏导数。然后将他们组成了一组向量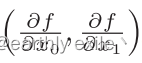，像这种由全部变量的偏导数组成的的向量我们称之为梯度（gradient）。

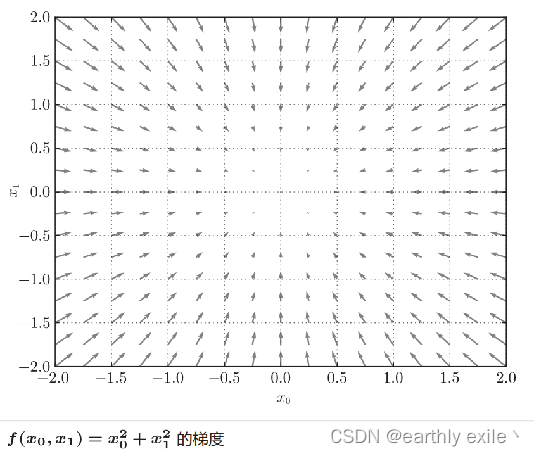
我们多取一些点，然后将视角变成俯视，我们发现所有的向量都变成了一个个箭头指向了中间最低处。此次引出我们的结论

        梯度总是指向函数值减少最多的方向。

梯度下降法

        机器学习的主要任务是在学习时寻找最优参数。同样地，神经网络也必须在学习时找到最优参数（权重和偏置）。这里所说的最优参数是指损失函数。取最小值时的参数。但是，一般而言，损失函数很复杂，参数空间庞大，我们不知道它在何处能取得最小值。而通过巧妙地使用梯度来寻找函数最小值或者尽可能小的值）的方法就是梯度下降法。这里需要注意的是，梯度表示的是各点处的函数值减小最多的方向。因此， 无法保证梯度所指的方向就是函数的最小值或者真正应该前进的方向。实际 上，在复杂的函数中，梯度指示的方向基本上都不是函数值最小处。

什么是鞍点

        

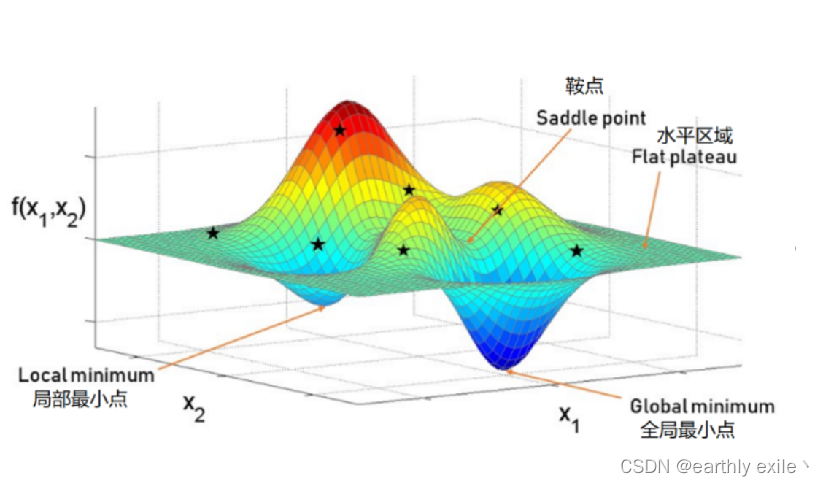
        函数的极小值、最小值以及被称为鞍点（saddle point）的地方， 梯度为 0。极小值是局部最小值，也就是限定在某个范围内的最 小值。鞍点是从某个方向上看是极大值，从另一个方向上看则是 极小值的点。虽然梯度法是要寻找梯度为 0的地方，但是那个地 方不一定就是最小值（也有可能是极小值或者鞍点）。此外，当函 数很复杂且呈扁平状时，学习可能会进入一个（几乎）平坦的地区， 陷入被称为“学习高原”的无法前进的停滞期。

        在梯度法中，函数的取值从当前位置沿着梯 度方向前进一定距离，然后在新的地方重新求梯度，再沿着新梯度方向前进， 如此反复，不断地沿梯度方向前进。像这样，通过不断地沿梯度方向前进， 逐渐减小函数值的过程就是梯度法（gradient method）。梯度法是解决机器 学习中最优化问题的常用方法，特别是在神经网络的学习中经常被使用。

        我们介绍了神经网络的学习，并通过数值微分计算了神经网络的权重参数的梯度（严格来说，是损失函数关于权重参数的梯度）。数值微分虽然简单，也容易实现，但缺点是计算上比较费时间。本章我们将学习一个能够高效计算权重参数的梯度的方法——误差反向传播法。

        误差反向传播法很重要，但是内容太多，这里不做介绍，后续我有空会单独开一篇来让大家系统学习。大家记住误差反向传播法是一种更高效的求梯度的方法，实际工程中都被机器学习框架实现，我们不需要手动写代码实现。

        到此神经网络所有的基础知识点都已经介绍完了。

常用的机器学习框架

        Keras：一个用 Python 编写的有效的高级神经网络应用程序编程接口 (API)。这个开源神经网络库旨在提供深度神经网络的快速实验，它可以在 CNTK、TensorFlow 和 Theano 之上运行。

        PyTorch：是一个相对较新的基于 Torch 的深度学习框架。由 Facebook 的 AI 研究小组开发并于 2017 年在 GitHub 上开源，用于自然语言处理应用程序。PyTorch 以简单、易用、灵活、高效的内存使用和动态计算图而闻名。它还让人感觉原生，使编码更易于管理并提高处理速度。         TensorFlow : 由 Google 开发并于 2015 年发布的端到端开源深度学习框架。它以文档和培训支持、可扩展的生产和部署选项、多个抽象级别以及对不同平台（例如 Android）的支持而闻名。

        实际工程中，我们可以选择机器学习框架来帮助我们实现神经网络，如PyTorch和TensorFlow,为了快速上手我们选择使用起来比较容易的pytorch。 PyTorch来取代大部分的底层工作，从而可以专注于网络的设计。PyTorch最强大且最便利的功能之一是，无论我们设想的网络是什么样子的，它都能替我们进行所有的微积分计算。即使设计改变了，PyTorch也会自动更新微积分计算，无须我们亲自动手计算梯度（gradient）。同时，PyTorch尽量在外观体验上与Python保持一致，以帮助Python用户快速上手。

pytorch初体验

        我们来看看如何使用pytorch实现下图这个神经网络模型

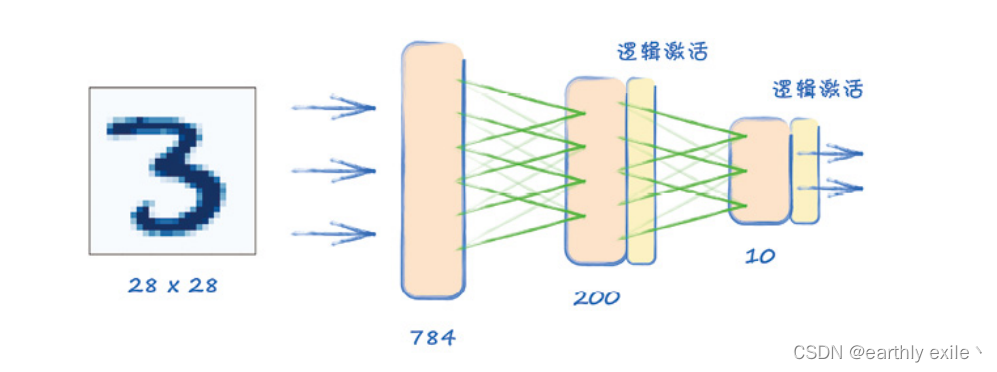
       未完待续。。。