cs231n assignment1

cs231n Assignment1

前言

​ 本文为 2024 年斯坦福 cs231n 作业一 的参考答案，代码框架可在官网下载，作业一包含 5 个问题：

1. k-Nearest Neighbor classifier
2. Training a Support Vector Machine
3. Implement a Softmax classifier
4. Two-Layer Neural Network
5. Higher Level Representations: Image Features

Q1: k-Nearest Neighbor classifier

​ kNN 分类器由两个阶段组成：

• 在训练期间，分类器获取训练数据并简单记忆。
• 在测试阶段，kNN 将每张测试图像与所有训练图像进行比较，并将最相似的 k 个训练实例的标签进行投票，从而对图像进行分类。
• k 值经过交叉验证。

​ cs231n 作业使用的数据集为 CIFAR-10，数据集包含 60000 张共 10 个类别的 32x32x3 的彩色图片，每个类别共有 6000 张图片，训练集包含 50000 张图片，测试集包含 10000 张图片，数据集详细介绍可参考 CIFAR-10 数据集官网。

​ kNN 分类器的训练代码如下：

class KNearestNeighbor(object):
    """ a kNN classifier with L2 distance """
    
    def train(self, X, y):
        """
        Train the classifier. For k-nearest neighbors this is just
        memorizing the training data.

        Inputs:
        - X: A numpy array of shape (num_train, D) containing the training data
          consisting of num_train samples each of dimension D.
        - y: A numpy array of shape (N,) containing the training labels, where
             y[i] is the label for X[i].
        """
        self.X_train = X
        self.y_train = y

​ 现在，我们想用 kNN 分类器对测试数据进行分类。我们可以将这一过程分为两个步骤：

1. 首先，我们必须计算所有测试示例和所有训练示例之间的距离。
2. 根据这些距离，我们为每个测试示例找出 k 个最近的示例，并让它们为标签投票，票数最高的标签即为预测结果。

compute_distances_two_loops

​ 使用两重 for 循环，计算所有测试示例和所有训练示例之间的距离，距离指标采用 L2 距离（欧几里得距离）：
$$d_2(I_1^p,I_2^p)=\sqrt{\sum _p(I_1^p-I_2^p{)}^2}$$
​ dists[i, j] 表示第 i 个测试图片与第 j 个训练图片的距离，实现思路为：

1. 遍历每一组测试图片和训练图片。
2. 通过表达式 np.sqrt(np.sum(np.square(X[i] - self.X_train[j]))) 计算每一组图片的 L2 距离。

def compute_distances_two_loops(self, X):
    """
    Compute the distance between each test point in X and each training point
    in self.X_train using a nested loop over both the training data and the
    test data.

    Inputs:
    - X: A numpy array of shape (num_test, D) containing test data.

    Returns:
    - dists: A numpy array of shape (num_test, num_train) where dists[i, j]
      is the Euclidean distance between the ith test point and the jth training
      point.
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in range(num_test):
        for j in range(num_train):
            #####################################################################
            # TODO:                                                             #
            # Compute the l2 distance between the ith test point and the jth    #
            # training point, and store the result in dists[i, j]. You should   #
            # not use a loop over dimension, nor use np.linalg.norm().          #
            #####################################################################
            # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
            
            dists[i, j] = np.sqrt(np.sum(np.square(X[i] - self.X_train[j])))
            
            # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    return dists

Inline Question 1：

​ 请注意距离矩阵中的结构模式，其中某些行或列明显更亮。(请注意，在默认配色方案中，黑色表示距离小，白色表示距离大）。

• 在数据中，是什么原因导致这些行明显变亮？
• 是什么导致了这些列？

【答】距离矩阵某一行明显更亮说明对应的测试图片与所有训练图片的 L2 距离都很大，距离矩阵某一列明显更亮说明对应的训练图片与所有测试图片的 L2 距离都很大。

predict_labels

​ 计算距离矩阵 dists 后，可以根据 dists 进行类别预测，实现思路为：

1. 遍历距离矩阵 dists 每一行。
2. 获取距离最近的 k 个训练图片的标签，存放在列表 closest_y 中。
3. 将 k 个距离最近的训练图片标签进行投票，票数最高的标签为预测结果。

def predict_labels(self, dists, k=1):
    """
    Given a matrix of distances between test points and training points,
    predict a label for each test point.

    Inputs:
    - dists: A numpy array of shape (num_test, num_train) where dists[i, j]
      gives the distance betwen the ith test point and the jth training point.

    Returns:
    - y: A numpy array of shape (num_test,) containing predicted labels for the
      test data, where y[i] is the predicted label for the test point X[i].
    """
    num_test = dists.shape[0]
    y_pred = np.zeros(num_test)
    for i in range(num_test):
        # A list of length k storing the labels of the k nearest neighbors to
        # the ith test point.
        closest_y = []
        #########################################################################
        # TODO:                                                                 #
        # Use the distance matrix to find the k nearest neighbors of the ith    #
        # testing point, and use self.y_train to find the labels of these       #
        # neighbors. Store these labels in closest_y.                           #
        # Hint: Look up the function numpy.argsort.                             #
        #########################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        closest_y = [self.y_train[i] for i in np.argsort(dists[i, :])[:k]]

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        #########################################################################
        # TODO:                                                                 #
        # Now that you have found the labels of the k nearest neighbors, you    #
        # need to find the most common label in the list closest_y of labels.   #
        # Store this label in y_pred[i]. Break ties by choosing the smaller     #
        # label.                                                                #
        #########################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        count = np.zeros(10)
        most_common_label, maxcount = -1, -1
        for label in closest_y:
          count[label] += 1
          if count[label] > maxcount:
            maxcount = count[label]
            most_common_label = label
        y_pred[i] = most_common_label

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    return y_pred

​ predict_labels 实现完成后，对 k=1 和 k=5 两种情况进行测试，分别得到的测试精度为 0.274、0.288。

Inline Question 2：

​ 我们还可以使用其他距离指标，如 L1 距离。记 $p_{ij}^{(k)}$ 为图片 $I_k$ 在位置 $(i,j)$ 处的像素值，所有图片的所有像素均值 $\mu$ 为：
$$\mu =\frac{1}{nhw}\sum _{k=1}^n\sum _{i=1}^h\sum _{j=1}^w{p}_{ij}^{(k)}$$
​ 所有图像的像素平均值 ${\mu }_{ij}$ 为：
$${\mu }_{ij}=\frac{1}{n}\sum _{k=1}^n{p}_{ij}^{(k)}$$
​ 所有图片的所有像素标准差 $\sigma$ 和所有图像的像素标准差 ${\sigma }_{ij}$ 的定义是类似的。

​ 以下哪些预处理步骤不会改变使用 L1 距离的 Nearest Neighbor 分类器的性能？请选择所有适用的步骤（训练和测试示例的预处理方式相同）。

1. 减去均值 $\mu$（${\widetilde{p_{ij}}}^{(k)}=p_{ij}^{(k)}-\mu$​）。

2. 减去每一个像素均值 ${\mu }_{ij}$（${\widetilde{p_{ij}}}^{(k)}=p_{ij}^{(k)}-{\mu }_{ij}$）。

3. 减去均值 $\mu$ 并除以标准差 $\sigma$。
   $${\widetilde{p_{ij}}}^{(k)}=\frac{p_{ij}^{(k)}-\mu }{\sigma }$$

4. 减去每一个像素均值 ${\mu }_{ij}$ 并除以像素标准差 ${\sigma }_{ij}$。
   $${\widetilde{p_{ij}}}^{(k)}=\frac{p_{ij}^{(k)}-{\mu }_{ij}}{{\sigma }_{ij}}$$

5. 旋转数据坐标轴，即以相同角度旋转所有图像。旋转造成的图像空白区域将填充相同的像素值，不进行插值处理。

【答】1、2、3、5。L1 距离公式为：
$$d_1(I_1,I_2)=\sum _p|I_1^p-I_2^p|$$
​ 若经过数据预处理后，$I_1^{p^{\prime }}-I_2^{p^{\prime }}=k(I_1^p-I_2^p)$（相对差值为原来的 k 倍, k > 0）时，不会对 Nearest Neighbor 分类器性能产生影响，因此 1、2、3、5 的预处理不会对 Nearest Neighbor 分类器产生影响。理由如下：

• 经过 1 或者 2 的预处理后，$I_1^{p^{\prime }}-I_2^{p^{\prime }}=I_1^p-I_2^p$，因此 L1 距离不变。
• 经过 3 的预处理后，$I_1^{p^{\prime }}-I_2^{p^{\prime }}=\frac{1}{\sigma }(I_1^p-I_2^p)$，L1 距离变为原来的 $\frac{1}{\sigma }$ 倍。
• 经过 5 的预处理后，原始区域对应的 L1 距离不变，新增的使用相同像素值填充的空白区域的像素差值为 0，因此总的 L1 距离不变。

compute_distances_one_loop

​ 使用一重 for 循环，计算所有测试示例和所有训练示例之间的距离，实现思路为：

1. 遍历每一张测试图片。
2. 通过表达式 np.sqrt(np.sum(np.square(X[i] - self.X_train), axis=1))，计算它与所有训练图片的 L2 距离，并存放于 dists[i, :] 中。

def compute_distances_one_loop(self, X):
    """
    Compute the distance between each test point in X and each training point
    in self.X_train using a single loop over the test data.

    Input / Output: Same as compute_distances_two_loops
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in range(num_test):
        #######################################################################
        # TODO:                                                               #
        # Compute the l2 distance between the ith test point and all training #
        # points, and store the result in dists[i, :].                        #
        # Do not use np.linalg.norm().                                        #
        #######################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        dists[i, :] = np.sqrt(np.sum(np.square(X[i] - self.X_train), axis=1))

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    return dists

​ 测试 compute_distances_one_loop 的实现，结果正确：

compute_distances_no_loops

​ 不使用 for 循环，计算所有测试示例和所有训练示例之间的距离，首先我们将 L2 距离公式进行如下变形，将括号展开：
$$\begin{array}{rl}{d}_2(I_1,I_2)& =\sqrt{\sum _p(I_1^p-I_2^p{)}^2}\\ & =\sqrt{\sum _p((I_1^p{)}^2-2I_1^p{I}_2^p+(I_2^p{)}^2)}\\ & =\sqrt{\sum _p(I_1^p{)}^2-2\sum _p{I}_1^p{I}_2^p+\sum _p(I_2^p{)}^2}\end{array}$$
​ 首先， dists[i, j] 表示第 i 个测试图片与第 j 个训练图片的 L2 距离。实现思路为：

1. 通过表达式 np.square(X), axis=1, keepdims=True) 计算 ${\sum }_p(I_1^p{)}^2$。
2. 通过表达式 np.sum(np.square(self.X_train), axis=1)) 计算 ${\sum }_p(I_2^p{)}^2$​。
3. 通过表达式 np.dot(X, self.X_train.T) 计算 ${\sum }_p{I}_1^p{I}_2^p$​。
4. 将 1、2、3 组合起来，利用广播机制计算 dists。

【注意】计算 ${\sum }_p(I_1^p{)}^2$ 时使用了带有 keepdims=True 参数的 np.sum 函数，目的是在计算 dists 时让其按列广播，具体原因与 dists 定义相关。

def compute_distances_no_loops(self, X):
    """
    Compute the distance between each test point in X and each training point
    in self.X_train using no explicit loops.

    Input / Output: Same as compute_distances_two_loops
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    #########################################################################
    # TODO:                                                                 #
    # Compute the l2 distance between all test points and all training      #
    # points without using any explicit loops, and store the result in      #
    # dists.                                                                #
    #                                                                       #
    # You should implement this function using only basic array operations; #
    # in particular you should not use functions from scipy,                #
    # nor use np.linalg.norm().                                             #
    #                                                                       #
    # HINT: Try to formulate the l2 distance using matrix multiplication    #
    #       and two broadcast sums.                                         #
    #########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    dists = np.sqrt(np.sum(np.square(X), axis=1, keepdims=True) 
                    - 2 * np.dot(X, self.X_train.T) 
                    + np.sum(np.square(self.X_train), axis=1))

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    return dists

​ 测试 compute_distances_no_loops 的实现，结果正确：

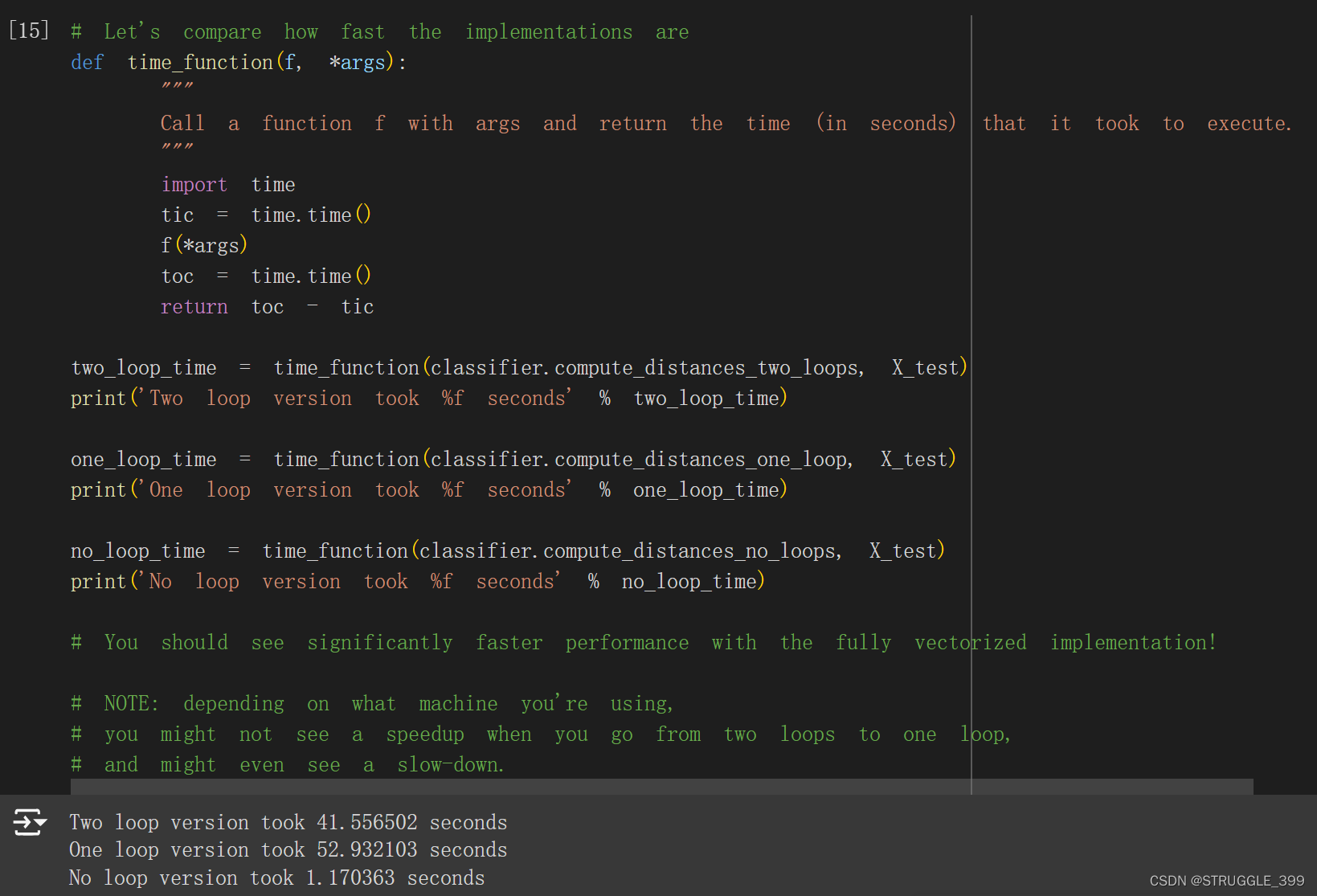
​ 最后，我们比较三个版本的距离计算时间，可以看到，不使用循环的版本（全向量化代码实现）快很多！

Cross Validation

​ K 折交叉验证的思想如下图所示（图示为 5 折交叉验证）：

1. 将训练数据分为 num_folds 份。
2. 将每一份作为验证集，剩余部分作为训练集，计算验证精度。
3. 计算平均验证精度。

​ 使用交叉验证进行超参数调整（Hyper parameter tuning）的步骤为：

1. 通过 numpy.array_split 函数将训练数据分为 num_folds 份。
2. 遍历每一组超参数，将每一份作为验证集，剩余部分作为训练集，计算验证精度，进而计算平均验证精度。
3. 选择平均验证精度最高对应的那一组超参数作为调参的结果。

num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]

X_train_folds = []
y_train_folds = []
################################################################################
# TODO:                                                                        #
# Split up the training data into folds. After splitting, X_train_folds and    #
# y_train_folds should each be lists of length num_folds, where                #
# y_train_folds[i] is the label vector for the points in X_train_folds[i].     #
# Hint: Look up the numpy array_split function.                                #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# 将训练集等分为 num_folds 份
X_train_folds = np.array_split(X_train, num_folds) 
y_train_folds = np.array_split(y_train, num_folds) 

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}


################################################################################
# TODO:                                                                        #
# Perform k-fold cross validation to find the best value of k. For each        #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times,   #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all     #
# values of k in the k_to_accuracies dictionary.                               #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

for k in k_choices:
  k_to_accuracies[k] = []
  for m in range(num_folds):
    # 使用第 m fold 作为 validation fold.
    knn = KNearestNeighbor()
    # 划分训练集和验证集
    X_train_set = np.concatenate(X_train_folds[:m] + X_train_folds[m+1:])
    y_train_set = np.concatenate(y_train_folds[:m] + y_train_folds[m+1:])
    X_validation_set = X_train_folds[m]
    y_validation_set = y_train_folds[m]

    knn.train(X_train_set, y_train_set)
    Y_preds = knn.predict(X_validation_set, k=k) # 获取预测结果
    acc = np.mean(Y_preds == y_validation_set) # 计算预测正确率
    k_to_accuracies[k].append(acc)

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# Print out the computed accuracies
for k in sorted(k_to_accuracies):
    for accuracy in k_to_accuracies[k]:
        print('k = %d, accuracy = %f' % (k, accuracy))

​ 最终的结果如下图所示，折线表示平均精度，由此可见 k=10 时平均验证精度最高，因此 best_k=10。

最终，我们设置 k=10，进行测试，得到测试精度为 28.8%，与题中描述一致。

Inline Question 3：

​ 在分类设置中，对于所有 k，以下哪些关于 k -Nearest Neighbor ( k -NN) 的说法是正确的？选择所有适用的。

1. k-NN 分类器的决策边界是线性的。
2. 1-NN 的训练误差总是低于或等于 5-NN 的误差。
3. 1-NN 的测试误差总是低于 5-NN 的测试误差。
4. 使用 k-NN 分类器对测试示例进行分类所需的时间随训练集的大小而增长。
5. 以上都不是。

【答】2、4，解释如下：

1. k-NN 分类器的决策边界是非线性的。
2. 1-NN 的训练误差始终为零，因为与其最近的图片就是其本身，因此训练误差为零，5-NN 的训练误差则不一定为零。
3. 不一定，5-NN 的测试误差可能更低。
4. k-NN 分类器在预测时，需要计算预测图片与所有训练图片的距离，因此分类时间随着训练集大小而增长。

Q2: Training a Support Vector Machine

​ SVM 分类器是线性分类器，为每一张测试图片计算一个得分向量，得分最高的类别即为 SVM 分类器预测的结果，得分向量的计算公式如下：
$$s=f(x,W,b)=Wx+b$$
​ 其中，$W$ 和 $b$ 为参数。SVM 分类器的损失函数（loss function）为：
$$L_i=\sum _{j\ne y_i}\max (0,s_j-s_{y_i}+\Delta )$$
​ 其中，$\Delta$ 为超参数，在该作业中 $\Delta =1$。SVM 分类器的代价函数（cost function）为：
$$L=\underset{\text{data loss}}{\underbrace{\frac{1}{N}\sum _i\sum _{j\ne y_i}\max (0,s_j-s_{y_i}+\Delta )}}+\underset{\text{regularization loss}}{\underbrace{\frac{1}{2}\lambda \sum _k\sum _l{W}_{k,l}^2}}$$
​ 其中，$\lambda$（正则化强度）为超参数，前面乘以 0.5 是因为在计算梯度时可以将其消除，无需在前面乘以梯度。

svm_loss_naive

​ 可参考 cs231n 课程笔记中的 SVM 损失函数的实现代码，其中包含完全非向量化的实现和半向量化的实现。

使用两个 for 循环，计算 SVM 损失，实现思路为：

1. 遍历每一张训练图片，计算对应的得分向量 scores，正确类别对应的得分 correct_class_score = scores[y[i]]。
2. 遍历每个类别的得分（正确类别得分除外），loss 累加上 margin = max(0, scores[j] - correct_class_score + 1)。
3. 当 magin > 0 时，出现非零项，需要更新 dW，dW 的第 j 列加上 X[i].T，第 y[i] 列减去 X[i].T。

def svm_loss_naive(W, X, y, reg):
    """
    Structured SVM loss function, naive implementation (with loops).

    Inputs have dimension D, there are C classes, and we operate on minibatches
    of N examples.

    Inputs:
    - W: A numpy array of shape (D, C) containing weights.
    - X: A numpy array of shape (N, D) containing a minibatch of data.
    - y: A numpy array of shape (N,) containing training labels; y[i] = c means
      that X[i] has label c, where 0 <= c < C.
    - reg: (float) regularization strength

    Returns a tuple of:
    - loss as single float
    - gradient with respect to weights W; an array of same shape as W
    """
    dW = np.zeros(W.shape)  # initialize the gradient as zero

    # compute the loss and the gradient
    num_classes = W.shape[1]
    num_train = X.shape[0]
    loss = 0.0
    #############################################################################
    # TODO:                                                                     #
    # Implement a unvectorized version of the structured SVM loss, storing the    #
    # result in loss.                                                           #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    for i in range(num_train):
        scores = X[i].dot(W)
        correct_class_score = scores[y[i]]
        for j in range(num_classes):
            if j == y[i]:
              continue
            margin = max(0, scores[j] - correct_class_score + 1)  # note delta = 1
            loss += margin
            if margin > 0:
              # 出现非零项, 与矩阵W的第j列和第y[i]列相关
              dW[:, j] += X[i]
              dW[:, y[i]] -= X[i]

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    # Right now the loss is a sum over all training examples, but we want it
    # to be an average instead so we divide by num_train.
    loss /= num_train
    dW /= num_train
    # Add regularization to the loss.
    loss += 0.5 * reg * np.sum(np.square(W))

    #############################################################################
    # TODO:                                                                     #
    # Compute the gradient of the loss function and store it dW.                #
    # Rather that first computing the loss and then computing the derivative,   #
    # it may be simpler to compute the derivative at the same time that the     #
    # loss is being computed. As a result you may need to modify some of the    #
    # code above to compute the gradient.                                       #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    # data loss的导数 + regularization loss 的导数就是 dW
    dW += reg * W

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    return loss, dW

【注意】上面的代码实现中没有涉及到参数 b，是因为进行了预处理操作，在图片向量添加了一个维度，其值固定为1，而参数矩阵 W 也增加一个维度，这一维就是原始的参数 b。

梯度推导

SVM 代价函数（cost function）为： $$L=\underset{\text{data loss}}{\underbrace{\frac{1}{N}\sum _i\sum _{j\ne y_i}\max (0,f(x_i;W{)}_j-f(x_i;W{)}_{y_i}+\Delta )}}+\underset{\text{regularization loss}}{\underbrace{\frac{1}{2}\lambda \sum _k\sum _l{W}_{k,l}^2}}$$ 由于： $$f(x_i;W{)}_j=x_{i1}{w}_{1j}+x_{i2}{w}_{2j}+\cdots +x_{iD}{w}_{Dj}$$ 因此，$f(x_i;W{)}_j$​ 与参数矩阵 W 的第 j 列有关： $$\frac{\partial }{\partial w_{kj}}f(x_i;W{)}_j=x_{ik},(1\le k\le D)$$ 同理，$f(x_i;W{)}_{y_i}$ 与参数矩阵 W 的第 yi 列有关，因此，在 margin = max(0, scores[j] - correct_class_score + 1) 大于 0 的情况下，需要更新 dW 的第 j 列和第 yi 列，分别加上 $x_i^T$、$-x_i^T$（其中 $x_i$ 为第 i 个训练图片向量（行向量））。

​ 运行梯度检查，测试结果如下，误差几乎为零，测试通过：

svm_loss_half_vectorized

​ 在实现全向量化实现前，先完成半向量化（仅使用一个 for 循环）的实现，实现的思路为：

1. 遍历每一个训练图片，计算得分向量 scores，正确类别对应的得分 correct_class_score = scores[y[i]]。。
2. 通过 np.maximum(0, scores - correct_class_score + 1) 计算 margins 向量，margins 的每个分量之和就是该训练图片的损失（注意需要 margins[y[i]] = 0）。
3. 将 margins 向量中每个大于 0 的分量置为 1（因为 dW 与 margins 的具体值无关，只要大于0即可）。
4. 将正确分类对应的 margins 分量置为 margins 向量大于 0 的分量个数的相反数。
5. dW 累加上 np.dot(X[i].reshape(-1, 1), margins)。

【注】该半向量化实现不是作业要求的，只是为了更平滑地过渡到全向量化代码的实现。前两步为损失计算，后三步为梯度计算。

def svm_loss_half_vectorized(W, X, y, reg):
    """
    Structured SVM loss function, vectorized implementation.

    Inputs and outputs are the same as svm_loss_naive.
    """
    loss = 0.0
    dW = np.zeros(W.shape)  # initialize the gradient as zero
    num_train = X.shape[0]
    num_classes = W.shape[1]

    for i in range(num_train):
        scores = X[i].dot(W)
        correct_class_score = scores[y[i]]
        margins = np.maximum(0, scores - correct_class_score + 1) # delta = 1
        margins[y[i]] = 0
        loss += np.sum(margins)

        margins[margins > 0] = 1
        margins[y[i]] = -np.sum(margins)
        dW += np.dot(X[i].reshape(-1, 1), margins)
    
    
    loss /= num_train
    dW /= num_train
    
    # 加上正则化项的损失和梯度
    loss += 0.5 * reg * np.sum(np.square(W))
    dW += reg * W
    
    return loss, dW

​ 由 svm_loss_naive 分析可知，当 margins[j] > 0 时， 矩阵 dW 的第 j 列和第 yi 列分别需要加上 $x_i^T$、$-x_i^T$，将 margins 进行第4、5 步的处理后，$x_i^T$ （列向量）与 margins（行向量）作矩阵乘法，得到的矩阵具有如下性质：

1. 若 margins[j] > 0，则得到的矩阵第 j 列为 $x_i^T$。
2. 矩阵第 yi 列为 -num 倍的 $x_i^T$，其中 num 为 margins 向量中分量大于零的个数。

将此矩阵加到 dW 即可完成一个训练图片的损失计算。

svm_loss_vectorized

​ 有了半向量化实现的思路，只需要做一些调整即可，不使用循环的实现的思路为：

1. 通过 X.dot(W)（矩阵乘法）， 计算得分矩阵 scores，获取每个训练图片正确分类类别的得分，存放于列表 correct_class_scores 中。
2. 通过 np.maximum(0, scores - correct_class_scores + 1) 计算 margins 矩阵，margins 的每个分量之和就是所有训练图片的损失（注意需要 margins[range(num_train), y] = 0）。
3. 将 margins 向量中每个大于 0 的分量置为 1。
4. 将正确分类对应的 margins 分量置为 margins 向量大于 0 的分量个数的相反数。
5. dW 累加上 np.dot(X.T, margins)。

def svm_loss_vectorized(W, X, y, reg):
    """
    Structured SVM loss function, vectorized implementation.

    Inputs and outputs are the same as svm_loss_naive.
    """
    loss = 0.0
    dW = np.zeros(W.shape)  # initialize the gradient as zero

    #############################################################################
    # TODO:                                                                     #
    # Implement a vectorized version of the structured SVM loss, storing the    #
    # result in loss.                                                           #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    num_train = X.shape[0]
    num_classes = W.shape[1]
    scores = np.dot(X, W)
    # 获取每个 x 正确分类类别的得分
    correct_class_scores = scores[range(num_train), y].reshape(-1, 1)
    margins = np.maximum(0, scores - correct_class_scores + 1)
    # 将正确分类的margins置为0
    margins[range(num_train), y] = 0
    loss += np.sum(margins) / num_train
    loss += 0.5 * reg * np.sum(np.square(W))

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    #############################################################################
    # TODO:                                                                     #
    # Implement a vectorized version of the gradient for the structured SVM     #
    # loss, storing the result in dW.                                           #
    #                                                                           #
    # Hint: Instead of computing the gradient from scratch, it may be easier    #
    # to reuse some of the intermediate values that you used to compute the     #
    # loss.                                                                     #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    margins[margins > 0] = 1
    margins[range(num_train),y] = -np.sum(margins, axis=1)
    dW += np.dot(X.T, margins) / num_train + reg * W

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    return loss, dW

​ 进行损失的测试，损失与 svm_loss_naive 的差异为零，测试通过：

​ 进行梯度的测试，梯度与 svm_loss_naive 的差异为零，测试通过：

Stochastic Gradient Descent (SGD)

​ 我们现在已经有了向量化的 SVM 损失实现，我们可以使用 SGD 最小化 SVM 代价函数。具体实现中，我们使用的是小批量随机梯度下降（minibatch SGD），实现的思路为：

1. 随机选择一部分训练样本（样本大小为 batch_size），通过 np.random.choice(num_train, size=batch_size) 可随机生成 [0, num_train-1] 之间的整数下标列表（长度为 batch_size）。
2. 根据这部分样本，计算 SVM 损失和梯度。
3. 运行梯度下降，进行参数 W 的更新。

def train(
        self,
        X,
        y,
        learning_rate=1e-3,
        reg=1e-5,
        num_iters=100,
        batch_size=200,
        verbose=False,
    ):
    """
    Train this linear classifier using stochastic gradient descent.

    Inputs:
    - X: A numpy array of shape (N, D) containing training data; there are N
      training samples each of dimension D.
    - y: A numpy array of shape (N,) containing training labels; y[i] = c
      means that X[i] has label 0 <= c < C for C classes.
    - learning_rate: (float) learning rate for optimization.
    - reg: (float) regularization strength.
    - num_iters: (integer) number of steps to take when optimizing
    - batch_size: (integer) number of training examples to use at each step.
    - verbose: (boolean) If true, print progress during optimization.

    Outputs:
    A list containing the value of the loss function at each training iteration.
    """
    num_train, dim = X.shape
    num_classes = (
        np.max(y) + 1
    )  # assume y takes values 0...K-1 where K is number of classes
    if self.W is None:
        # lazily initialize W
        self.W = 0.001 * np.random.randn(dim, num_classes)

    # Run stochastic gradient descent to optimize W
    loss_history = []
    for it in range(num_iters):
        X_batch = None
        y_batch = None

        #########################################################################
        # TODO:                                                                 #
        # Sample batch_size elements from the training data and their           #
        # corresponding labels to use in this round of gradient descent.        #
        # Store the data in X_batch and their corresponding labels in           #
        # y_batch; after sampling X_batch should have shape (batch_size, dim)   #
        # and y_batch should have shape (batch_size,)                           #
        #                                                                       #
        # Hint: Use np.random.choice to generate indices. Sampling with         #
        # replacement is faster than sampling without replacement.              #
        #########################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        idxs = np.random.choice(num_train, size=batch_size)
        X_batch, y_batch = X[idxs], y[idxs]

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        # evaluate loss and gradient
        loss, grad = self.loss(X_batch, y_batch, reg)
        loss_history.append(loss)

        # perform parameter update
        #########################################################################
        # TODO:                                                                 #
        # Update the weights using the gradient and the learning rate.          #
        #########################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        self.W = self.W - learning_rate * grad

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        if verbose and it % 100 == 0:
            print("iteration %d / %d: loss %f" % (it, num_iters, loss))

    return loss_history

​ 运行测试，SGD 的每一次迭代，SVM 的损失呈下降趋势，算法正确：

​ 损失随迭代次数的变化如下图所示：

​ 线性分类器的预测函数特别简单，实现思路如下：

1. 计算得分矩阵 scores。
2. 预测类别就是得分向量中分量最大的下标，通过 numpy.argmax 实现。

def predict(self, X):
    """
    Use the trained weights of this linear classifier to predict labels for
    data points.

    Inputs:
    - X: A numpy array of shape (N, D) containing training data; there are N
      training samples each of dimension D.

    Returns:
    - y_pred: Predicted labels for the data in X. y_pred is a 1-dimensional
      array of length N, and each element is an integer giving the predicted
      class.
    """
    y_pred = np.zeros(X.shape[0])
    ###########################################################################
    # TODO:                                                                   #
    # Implement this method. Store the predicted labels in y_pred.            #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    scores = np.dot(X, self.W) # 计算得分
    y_pred = np.argmax(scores, axis=1)

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    return y_pred

​ 运行测试，可得训练精度和验证精度：

​ 接下来进行超参数调整（Hyperparameter tuning），修改原始的 learning_rates 和 regularization_strengths 列表，增加更多的超参数以供搜索。实现的思路如下：

1. 遍历每一组超参数，在该超参数设定下进行 SVM 的训练。
2. 进行预测，计算训练精度、验证精度。
3. 记录最佳验证精度，以及对应的 SVM 分类器。

# Use the validation set to tune hyperparameters (regularization strength and
# learning rate). You should experiment with different ranges for the learning
# rates and regularization strengths; if you are careful you should be able to
# get a classification accuracy of about 0.39 (> 0.385) on the validation set.

# Note: you may see runtime/overflow warnings during hyper-parameter search.
# This may be caused by extreme values, and is not a bug.

# results is dictionary mapping tuples of the form
# (learning_rate, regularization_strength) to tuples of the form
# (training_accuracy, validation_accuracy). The accuracy is simply the fraction
# of data points that are correctly classified.
results = {}
best_val = -1   # The highest validation accuracy that we have seen so far.
best_svm = None # The LinearSVM object that achieved the highest validation rate.

################################################################################
# TODO:                                                                        #
# Write code that chooses the best hyperparameters by tuning on the validation #
# set. For each combination of hyperparameters, train a linear SVM on the      #
# training set, compute its accuracy on the training and validation sets, and  #
# store these numbers in the results dictionary. In addition, store the best   #
# validation accuracy in best_val and the LinearSVM object that achieves this  #
# accuracy in best_svm.                                                        #
#                                                                              #
# Hint: You should use a small value for num_iters as you develop your         #
# validation code so that the SVMs don't take much time to train; once you are #
# confident that your validation code works, you should rerun the validation   #
# code with a larger value for num_iters.                                      #
################################################################################

# Provided as a reference. You may or may not want to change these hyperparameters
learning_rates = [1e-7, 3e-7, 1e-6, 3e-6, 1e-5, 3e-5, 1e-4, 3e-4, 1e-3, 3e-3, 1e-2, 3e-2]
regularization_strengths = [1e4, 1.5e4, 2e4, 2.5e4, 3e4, 3.5e4, 4e4, 4.5e4, 5e4]

# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

for lr in learning_rates:
  for reg in regularization_strengths:
    svm = LinearSVM()
    loss_hist = svm.train(X_train, y_train, learning_rate=lr, reg=reg,
                      num_iters=500, verbose=True)
    y_train_pred = svm.predict(X_train)
    y_val_pred = svm.predict(X_val)
    training_accuracy = np.mean(y_train == y_train_pred)
    validation_accuracy = np.mean(y_val == y_val_pred)
    results[(lr, reg)] = (training_accuracy, validation_accuracy)

    if best_val < validation_accuracy:
      best_val = validation_accuracy
      best_svm = svm

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# Print out results.
for lr, reg in sorted(results):
    train_accuracy, val_accuracy = results[(lr, reg)]
    print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
                lr, reg, train_accuracy, val_accuracy))

print('best validation accuracy achieved during cross-validation: %f' % best_val)

​ 结果如下图所示：

​ 利用 best_svm 进行预测，测试精度为 37.4%。

​ 最后，将 SVM 学习到的权重参数 W 进行可视化：

​ 可视化结果如下：

Inline Question 2

​ 描述可视化 SVM 权重的外观，并简要解释其外观的原因。

【答】SVM 权重的外观与对应类别的图片形状相似，比较明显的类别是 car、frog、horse 等。出现这种外观的原因是因为 SVM 分类器实质上是在做模板匹配，SVM 分类器在训练时会为每一个类别的图片学习一个模板，这个模板会平均同一类别的所有图片的差异。

Q3: Implement a Softmax classifier

​ Softmax 分类器也是一个线性分类器，与 SVM 分类器的区别是其损失函数不同，Softmax 的损失函数为交叉熵函数（cross entropy function）：
$$L_i=-\log (\frac{e^{f_{y_i}}}{{\sum }_j{e}^{f_j}})=\log (\sum _j{e}^{f_j})-f_{y_i}$$
​ Softmax 分类器的代价函数为：
$$L=\underset{\text{data loss}}{\underbrace{\frac{1}{N}\sum _i[\log (\sum _j{e}^{f_j})-f_{y_i}]}}+\underset{\text{regularization loss}}{\underbrace{\frac{1}{2}\lambda \sum _k\sum _l{W}_{k,l}^2}}$$
​ 损失函数梯度推导
$$\frac{\partial }{\partial w_{kl}}{L}_i=\{\begin{array}{ll}\frac{e^{f_l}}{{\sum }_j{e}^{f_j}}{x}_{ik}=p_l{x}_{ik}& \text{if }l\ne y_i\\ \frac{e^{f_l}}{{\sum }_j{e}^{f_j}}{x}_{ik}-x_{ik}=(p_l-1)x_{ik}& \text{if }l=y_i\end{array}$$
​ 其中，$1\le k\le D$，整理后可得：
$$\frac{\partial }{\partial w_{kl}}{L}_i=\{\begin{array}{ll}{p}_l{x}_{ik}& \text{if }l\ne y_i\\ (p_l-1)x_{ik}& \text{if }l=y_i\end{array}$$

softmax_loss_naive

​ 梯度的推导过程如上所示，实现的思路为：

1. 首先计算得分向量 score，然后将 score 的每一个分量减去最大分量值，保证数值稳定性（这一步不会影响损失和梯度）。
2. 为了便于计算梯度，通过 p[y[i]] -= 1 统一形式。
3. 将 np.dot(X[i].reshape(-1, 1), p.reshape(1, -1)) 累加到 dW。

def softmax_loss_naive(W, X, y, reg):
    """
    Softmax loss function, naive implementation (with loops)

    Inputs have dimension D, there are C classes, and we operate on minibatches
    of N examples.

    Inputs:
    - W: A numpy array of shape (D, C) containing weights.
    - X: A numpy array of shape (N, D) containing a minibatch of data.
    - y: A numpy array of shape (N,) containing training labels; y[i] = c means
      that X[i] has label c, where 0 <= c < C.
    - reg: (float) regularization strength

    Returns a tuple of:
    - loss as single float
    - gradient with respect to weights W; an array of same shape as W
    """
    # Initialize the loss and gradient to zero.
    loss = 0.0
    dW = np.zeros_like(W)

    #############################################################################
    # TODO: Compute the softmax loss and its gradient using explicit loops.     #
    # Store the loss in loss and the gradient in dW. If you are not careful     #
    # here, it is easy to run into numeric instability. Don't forget the        #
    # regularization!                                                           #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    num_train = X.shape[0]
    num_classes = W.shape[1]
    for i in range(num_train):
      score = X[i].dot(W)
      score -= max(score) # 防止溢出，保证数值稳定性
      p = np.exp(score) / np.sum(np.exp(score))
      loss += -np.log(p[y[i]])

      p[y[i]] -= 1 # 统一形式
      for j in range(num_classes):
        dW[:, j] += p[j] * X[i]


    loss /= num_train
    loss += 0.5 * reg * np.sum(np.square(W))
    dW /= num_train
    dW += reg * W
    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    return loss, dW

​ 测试结果如下，与预期结果相近：

Inline Question 1

​ 为什么我们预计损失接近-log(0.1)？请简要解释。

【答】因为我们随机产生参数 W，因而分类也是随机的，CIFAR-10 共有 10 个类别的图片，因此分类正确的概率为 10%，所以 softmax loss 应该接近 -log(0.1)。

梯度测试如下，解析梯度和数值梯度相差几乎为零，梯度测试通过：

softmax_loss_half_vectorized

​ 该实现为半向量化实现，作业中没有要求此实现，实际上就是使用一个 for 循环计算损失和梯度，主要是为了更好地过渡到全向量化代码的实现。

​ softmax_loss_naive 内层循环是很容易优化的，只需要计算 $x_i^T$ 与 p 的乘积（矩阵乘法），加到 dW 即可。

def softmax_loss_half_vectorized(W, X, y, reg):
    """
    Softmax loss function, naive implementation (with loops)

    Inputs have dimension D, there are C classes, and we operate on minibatches
    of N examples.

    Inputs:
    - W: A numpy array of shape (D, C) containing weights.
    - X: A numpy array of shape (N, D) containing a minibatch of data.
    - y: A numpy array of shape (N,) containing training labels; y[i] = c means
      that X[i] has label c, where 0 <= c < C.
    - reg: (float) regularization strength

    Returns a tuple of:
    - loss as single float
    - gradient with respect to weights W; an array of same shape as W
    """
    # Initialize the loss and gradient to zero.
    loss = 0.0
    dW = np.zeros_like(W)

    #############################################################################
    # TODO: Compute the softmax loss and its gradient using explicit loops.     #
    # Store the loss in loss and the gradient in dW. If you are not careful     #
    # here, it is easy to run into numeric instability. Don't forget the        #
    # regularization!                                                           #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    num_train = X.shape[0]
    num_classes = W.shape[1]
    for i in range(num_train):
      score = X[i].dot(W)
      score -= max(score) # 防止溢出，保证数值稳定性
      p = np.exp(score) / np.sum(np.exp(score))
      loss += -np.log(p[y[i]])

      p[y[i]] -= 1
      dW += np.dot(X[i].reshape(-1, 1), p.reshape(1, -1))


    loss /= num_train
    loss += 0.5 * reg * np.sum(np.square(W))
    dW /= num_train
    dW += reg * W

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    return loss, dW

softmax_loss_vectorized

​ 完成半向量化实现后，做一些调整即可完成全向量化实现，实现思路如下：

1. 计算得分矩阵 scores，将 scores 做与 softmax_loss_naive相同的处理，以保证数值稳定性（这一步不会影响损失和梯度）。
2. 计算概率矩阵 p。
3. 剩下的损失、梯度计算与 softmax_loss_half_vectorized 类似。

def softmax_loss_vectorized(W, X, y, reg):
    """
    Softmax loss function, vectorized version.

    Inputs and outputs are the same as softmax_loss_naive.
    """
    # Initialize the loss and gradient to zero.
    loss = 0.0
    dW = np.zeros_like(W)

    #############################################################################
    # TODO: Compute the softmax loss and its gradient using no explicit loops.  #
    # Store the loss in loss and the gradient in dW. If you are not careful     #
    # here, it is easy to run into numeric instability. Don't forget the        #
    # regularization!                                                           #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    num_train, dim = X.shape
    num_classes = W.shape[1]

    scores = X.dot(W) # 得分矩阵
    scores -= np.max(scores, axis=1, keepdims=True)
    p = np.exp(scores) / np.sum(np.exp(scores), axis=1, keepdims=True)
    loss += np.sum(-np.log(p[range(num_train), y])) / num_train + 0.5 * reg * np.sum(np.square(W))

    p[range(num_train), y] -= 1
    dW += np.dot(X.T, p) / num_train + reg * W
    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    return loss, dW

​ 最后进行超参数调整（Hyperparameter tuning）：

# Use the validation set to tune hyperparameters (regularization strength and
# learning rate). You should experiment with different ranges for the learning
# rates and regularization strengths; if you are careful you should be able to
# get a classification accuracy of over 0.35 on the validation set.

from cs231n.classifiers import Softmax
results = {}
best_val = -1
best_softmax = None

################################################################################
# TODO:                                                                        #
# Use the validation set to set the learning rate and regularization strength. #
# This should be identical to the validation that you did for the SVM; save    #
# the best trained softmax classifer in best_softmax.                          #
################################################################################

# Provided as a reference. You may or may not want to change these hyperparameters
learning_rates = [1e-7, 3e-7, 1e-6]
regularization_strengths = [1e4, 2.5e4, 5e4, 1e5]

# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

for lr in learning_rates:
  for reg in regularization_strengths:
    softmax = Softmax()
    softmax.train(X_train, y_train, learning_rate=lr, reg=reg)
    y_train_pred = softmax.predict(X_train)
    y_val_pred = softmax.predict(X_val)
    training_accuracy = np.mean(y_train == y_train_pred)
    validation_accuracy = np.mean(y_val_pred == y_val)
    results[(lr, reg)] = (training_accuracy, validation_accuracy)
    if best_val < validation_accuracy:
      best_val = validation_accuracy
      best_softmax = softmax

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# Print out results.
for lr, reg in sorted(results):
    train_accuracy, val_accuracy = results[(lr, reg)]
    print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
                lr, reg, train_accuracy, val_accuracy))

print('best validation accuracy achieved during cross-validation: %f' % best_val)

​ 测试的结果如下，获取的最高验证精度接近 38.4%。

​ 在测试集中测试，获取测试精度为 37.3%。

​ Softmax 分类器学习到的权重可视化如下，结果与 SVM 分类器学习到的权重可视化图相近。

Q4: Two-Layer Neural Network

​ 在本练习中，我们将采用模块化方法实现全连接网络（fully-connected neural network）。我们将为每一层实现一个 forward 和 backward 函数。forward 函数将接收输入、权重和其他参数，并返回输出和 cache 对象，cache 对象中存储了后向传递所需的数据，就像下面这样：

def layer_forward(x, w):
  """ Receive inputs x and weights w """
  # Do some computations ...
  z = # ... some intermediate value
  # Do some more computations ...
  out = # the output

  cache = (x, w, z, out) # Values we need to compute gradients

  return out, cache

后向传递将接收上游导数和 cache 对象，并返回相对于输入和权重的梯度，就像这样：

def layer_backward(dout, cache):
  """
  Receive dout (derivative of loss with respect to outputs) and cache,
  and compute derivative with respect to inputs.
  """
  # Unpack cache values
  x, w, z, out = cache

  # Use values in cache to compute derivatives
  dx = # Derivative of loss with respect to x
  dw = # Derivative of loss with respect to w

  return dx, dw

affine layer

affine_forward

​ 首先实现的是仿射层（affine layer）的前向函数，仿射层做的变换为仿射变换，形式为：
$$y=wx+b$$
​ 具体的实现思路为：

1. 将 x 变换形状，将每一行延展成一个行向量，最终 x 变换为矩阵，其形状为 (N, D)。
2. 通过 np.dot(x, w) + b 即可完成仿射变换。

def affine_forward(x, w, b):
    """
    Computes the forward pass for an affine (fully-connected) layer.

    The input x has shape (N, d_1, ..., d_k) and contains a minibatch of N
    examples, where each example x[i] has shape (d_1, ..., d_k). We will
    reshape each input into a vector of dimension D = d_1 * ... * d_k, and
    then transform it to an output vector of dimension M.

    Inputs:
    - x: A numpy array containing input data, of shape (N, d_1, ..., d_k)
    - w: A numpy array of weights, of shape (D, M)
    - b: A numpy array of biases, of shape (M,)

    Returns a tuple of:
    - out: output, of shape (N, M)
    - cache: (x, w, b)
    """
    out = None
    ###########################################################################
    # TODO: Implement the affine forward pass. Store the result in out. You   #
    # will need to reshape the input into rows.                               #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    out = np.dot(np.reshape(x, (x.shape[0], -1)), w) + b

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = (x, w, b)
    return out, cache

​ 测试结果如下：

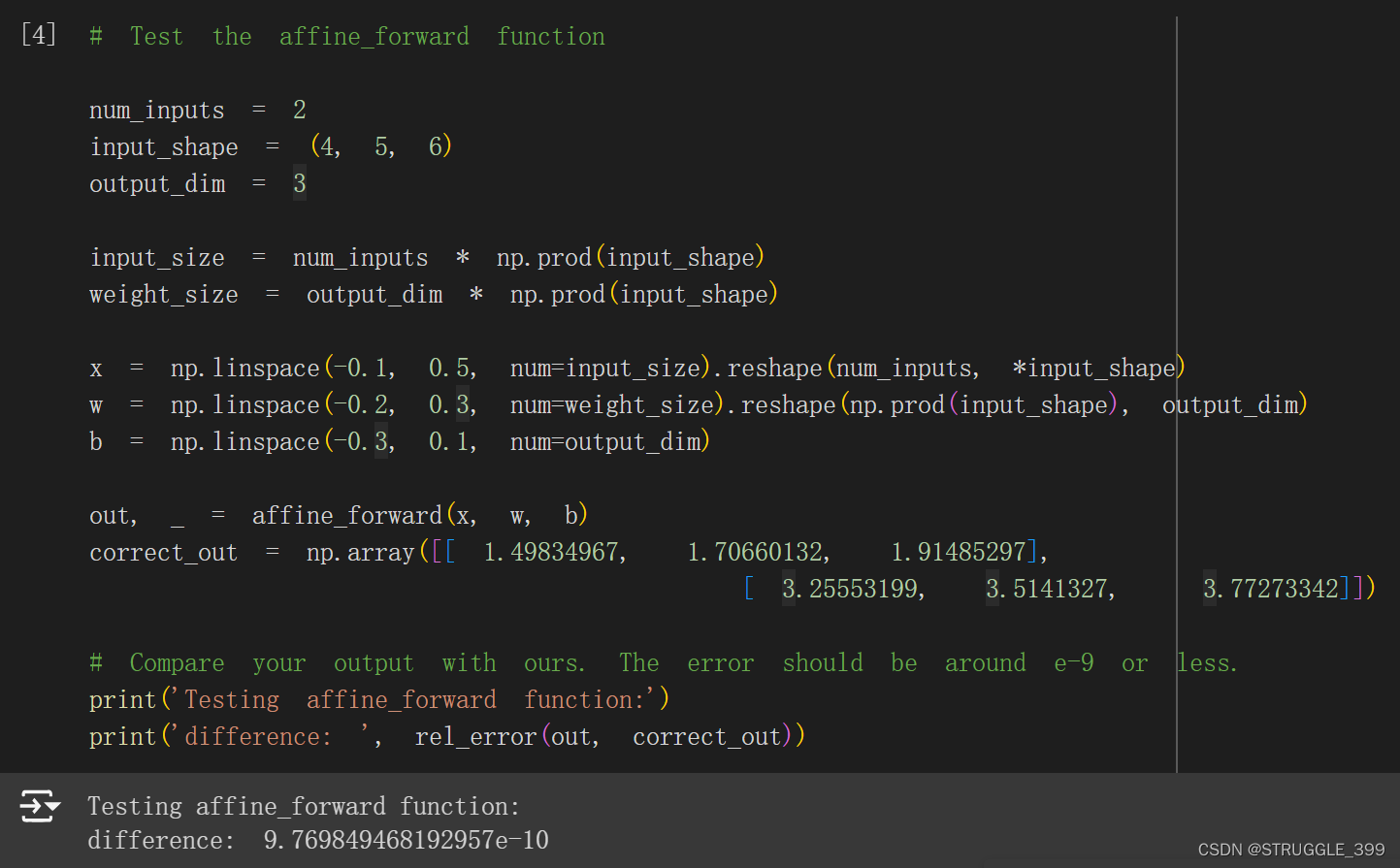
affine_backward

​ 接下来实现的是仿射层（affine layer）的后向函数，仿射层实际的计算公式为：
$$y=xw+b$$
​ 其中 x 为形如 (N, D) 的矩阵， w 为形如 (D, M) 的矩阵，b 为 形如(M, )的行向量，具体计算时会利用广播机制。

​ 下面为梯度推导过程，首先定义几个符号：
$$\begin{gathered} X=\left(\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1D}\\ x_{21}& x_{22}& \cdots & x_{2D}\\ ⋮& ⋮& & ⋮\\ x_{N1}& x_{N2}& \cdots & x_{ND}\end{array}\right)W=\left(\begin{array}{cccc}{w}_{11}& w_{12}& \cdots & w_{1M}\\ w_{21}& w_{22}& \cdots & w_{2M}\\ ⋮& ⋮& & ⋮\\ w_{D1}& w_{D2}& \cdots & w_{DM}\end{array}\right)Y=\left(\begin{array}{cccc}{y}_{11}& y_{12}& \cdots & y_{1M}\\ y_{21}& y_{22}& \cdots & y_{2M}\\ ⋮& ⋮& & ⋮\\ y_{N1}& y_{N2}& \cdots & y_{NM}\end{array}\right) \\ b=\left(\begin{array}{cccc}{b}_1& b_2& \cdots & b_M\end{array}\right) \end{gathered}$$

​ 根据仿射变换的公式，我们不难得到：
$$y_{ij}=\sum _k{x}_{ik}{w}_{kj}+b_j$$
​ 其中 $1\le i\le N,1\le j\le M$，我们可以得到，$y_{ij}$ 与 矩阵 $X$ 的第 i 行、矩阵 $W$ 的第 j 列以及向量 $b$ 的第 j 个分量有关，因此：
$$\frac{\partial y_{ij}}{\partial x_{ik}}=w_{kj},\frac{\partial y_{ij}}{\partial x_{kj}}=x_{ik},\frac{\partial y_{ij}}{\partial b_j}=1$$
​ 根据链式法则，我们可以得到 dx、dw、db 的梯度：
$$\frac{\partial L}{\partial b_j}=\sum _{k}d{y}_{kj}(1\le k\le M)$$

$$\frac{\partial L}{\partial x_{ij}}=\sum _k{w}_{jk}d{y}_{ik}(1\le k\le M)$$

$$\frac{\partial L}{\partial w_{ij}}=\sum _k{x}_{ki}d{y}_{kj}(1\le k\le N)$$

​ 根据以上分析，我们可以得到 dx、dw、db 的计算方法如下：
$$\frac{\partial L}{\partial X}=dY\ast W^T,\frac{\partial L}{\partial W}=X^T\ast dY$$

$$\frac{\partial L}{\partial b}=\left(\begin{array}{cccc}{\sum }_{k}d{y}_{k1}& {\sum }_{k}d{y}_{k2}& \cdots & {\sum }_{k}d{y}_{kM}\end{array}\right)$$

​ 有了计算公式后，具体实现如下：

def affine_backward(dout, cache):
    """
    Computes the backward pass for an affine layer.

    Inputs:
    - dout: Upstream derivative, of shape (N, M)
    - cache: Tuple of:
      - x: Input data, of shape (N, d_1, ... d_k)
      - w: Weights, of shape (D, M)
      - b: Biases, of shape (M,)

    Returns a tuple of:
    - dx: Gradient with respect to x, of shape (N, d1, ..., d_k)
    - dw: Gradient with respect to w, of shape (D, M)
    - db: Gradient with respect to b, of shape (M,)
    """
    x, w, b = cache
    dx, dw, db = None, None, None
    ###########################################################################
    # TODO: Implement the affine backward pass.                               #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    dx = np.reshape(np.dot(dout, w.T), x.shape)
    dw = np.dot(np.reshape(x, (x.shape[0], -1)).T, dout)
    db = np.sum(dout, axis=0)

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx, dw, db

​ 梯度测试如下：

ReLU activation layer

​ ReLU 激活函数的公式如下：
$$\sigma (x)=\max (0,x)$$
​ ReLU 函数的梯度为：
$$\frac{d\sigma }{dx}=\{\begin{array}{ll}0& \text{if }x\le 0\\ 1& \text{if }x>0\end{array}$$

relu_forward

​ ReLU 层的前向函数实现特别简单，就是通过 np.maximum(0, x) 即可实现 ReLU 激活函数。

def relu_forward(x):
    """
    Computes the forward pass for a layer of rectified linear units (ReLUs).

    Input:
    - x: Inputs, of any shape

    Returns a tuple of:
    - out: Output, of the same shape as x
    - cache: x
    """
    out = None
    ###########################################################################
    # TODO: Implement the ReLU forward pass.                                  #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    out = np.maximum(0, x)

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = x
    return out, cache

​ ReLU 前向函数测试如下：

relu_backward

​ 根据 ReLU 激活函数的导数公式，可得 ReLU 层的反向函数实现思路为：

1. 通过 x > 0 生成一个布尔矩阵。
2. dout * (x > 0) 就是 dx，这一步操作是一个过滤功能，将原来 x < 0 的元素对应的梯度置零。

def relu_backward(dout, cache):
    """
    Computes the backward pass for a layer of rectified linear units (ReLUs).

    Input:
    - dout: Upstream derivatives, of any shape
    - cache: Input x, of same shape as dout

    Returns:
    - dx: Gradient with respect to x
    """
    dx, x = None, cache
    ###########################################################################
    # TODO: Implement the ReLU backward pass.                                 #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    dx = dout * (x > 0)

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx

​ ReLU 层后向函数测试如下：

Inline Question 1

​ 我们只要求你实现 ReLU，但在神经网络中可以使用多种不同的激活函数，每种函数都有其优缺点。特别是，激活函数常见的一个问题是在反向传播过程中梯度流为零（或接近零）。以下哪些激活函数存在这个问题？如果在一维情况下考虑这些函数，哪些类型的输入会导致这种行为？

1. Sigmoid
2. ReLU
3. Leaky ReLU

【答】1、2。

1. Sigmoid 激活函数形式为：
   $$\sigma (x)=\frac{1}{1+e^{-x}}$$
   Sigmoid 函数图像如下所示，当 x 的绝对值充分大时，其梯度接近于零。

   

2. ReLU 激活函数形式为：
   $$\sigma (x)=\max (0,x)$$
   在 x 的正半轴中，ReLU 函数不会饱和，因此梯度不会为零，而在 x 的负半轴中，ReLU 函数的梯度为零。

   

3. Leaky ReLU 激活函数形式为：
   $$\sigma (x)=\max (\alpha x,x)$$
   Leaky ReLU 函数不会饱和，因此梯度不会为零（或接近零）。

   

“Sandwich” layers

​ 所谓的 “三明治” 层，就是将若干层组合起来形成一个更大的层，例如仿射层（affine layer）后跟一个 ReLU 非线性层。实现思路如下：

• affine_relu_forward 可以用 affine_forward 和 relu_forward 实现。
• affine_relu_backward 可以用 affine_backward 和 relu_backward 实现。

affine_relu_forward

​ 注意调用次序，首先调用 affine_forward，在调用 relu_forward。

def affine_relu_forward(x, w, b):
    """
    Convenience layer that perorms an affine transform followed by a ReLU

    Inputs:
    - x: Input to the affine layer
    - w, b: Weights for the affine layer

    Returns a tuple of:
    - out: Output from the ReLU
    - cache: Object to give to the backward pass
    """
    a, fc_cache = affine_forward(x, w, b)
    out, relu_cache = relu_forward(a)
    cache = (fc_cache, relu_cache)
    return out, cache

affine_relu_backward

​ 注意调用顺序，首先调用 relu_backward，再调用 affine_backward 。

def affine_relu_backward(dout, cache):
    """
    Backward pass for the affine-relu convenience layer
    """
    fc_cache, relu_cache = cache
    da = relu_backward(dout, relu_cache)
    dx, dw, db = affine_backward(da, fc_cache)
    return dx, dw, db

​ 测试结果如下：

loss layers

​ loss 层的 softmax 层、svm 层的损失、梯度的计算与前面的 softmax_loss、svm_loss 的实现非常类似，区别在于：

• softmax 层、svm 层的输入 x 就是得分矩阵 scores（不再是 x 和 参数 w、b）。
• 得益于反向传播算法，梯度的计算不再需要直接计算相对于神经网络的输入梯度，只需要相对于得分矩阵的梯度。

softmax layer

​ loss 的计算同 Q3 的 softmax_loss_vectorized 计算方式相同，而梯度的计算则更为简单，只需要计算损失相对于得分的梯度。Softmax 分类器的代价函数为：
$$L=\frac{1}{N}\sum _i[\log (\sum _j{e}^{f(x_i,W{)}_j})-f(x_i,W{)}_{y_i}]$$
​ 其中，x[i, j] 就是 $f(x_i,W{)}_j$。因此梯度推导如下：
KaTeX parse error: Undefined control sequence: \part at position 8: \frac{\̲p̲a̲r̲t̲ ̲L}{\part x_{ij}…
​ 整理后可得：
$$\frac{\partial L}{\partial x_{ij}}=\{\begin{array}{ll}\frac{1}{N}{p}_{ij}& \text{ if }j\ne y_i\\ \frac{1}{N}(p_{ij}-1)& \text{ if }j=y_i\end{array}$$
​ 因此在计算完损失后，通过 p[range(num_train), y] -= 1 统一形式，之后 p / N 即为所求的损失对得分的梯度值。

def softmax_loss(x, y):
    """
    Computes the loss and gradient for softmax classification.

    Inputs:
    - x: Input data, of shape (N, C) where x[i, j] is the score for the jth
      class for the ith input.
    - y: Vector of labels, of shape (N,) where y[i] is the label for x[i] and
      0 <= y[i] < C

    Returns a tuple of:
    - loss: Scalar giving the loss
    - dx: Gradient of the loss with respect to x
    """
    loss, dx = None, None
    
    ###########################################################################
    # TODO: Copy over your solution from A1.
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    N, C = x.shape
    x = x - np.max(x, axis=1, keepdims=True) # 保证数值稳定性
    p = np.exp(x) / np.sum(np.exp(x), axis=1, keepdims=True)
    loss = np.sum(-np.log(p[range(N), y])) / N

    p[range(N), y] -= 1
    dx = p / num_train

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return loss, dx

svm layer

​ loss 的计算同 Q2 的 svm_loss_vectorized 计算方式相同，同 softmax layer 一样，只需要计算损失相对于得分的梯度。svm 的代价函数定义为：
$$\begin{array}{rl}L& =\frac{1}{N}\sum _i\sum _{j\ne y_i}\max (0,s_j-s_{y_i}+\Delta )\\ & =\frac{1}{N}\sum _i\sum _{j\ne y_i}\max (0,f(x_i,W{)}_j-f(x_i,W{)}_{y_i}+\Delta )\end{array}$$
​ 其中，x[i, j] 就是 $f(x_i,W{)}_j$。

​ 当 $j\ne y_i$ 时，
$$\frac{\partial L}{\partial x_{ij}}=\{\begin{array}{ll}\frac{1}{N}& \text{if }f(x_i,W{)}_j-f(x_i,W{)}_{y_i}+\Delta >0\\ 0& \text{otherwise}\end{array}$$
​ 当 $j=y_i$ 时，
$$\frac{\partial L}{\partial x_{i{y}_i}}=\sum _{j\ne y_i}\frac{\partial L}{\partial x_{ij}}$$
​ 因此梯度计算的实现思路为：

1. margins[margins > 0] = 1，将 margins 中所有大于零元素置为 1。
2. margins[range(N), y] = -np.sum(margins, axis=1) 。
3. dx = margins / N。

def svm_loss(x, y):
    """
    Computes the loss and gradient using for multiclass SVM classification.

    Inputs:
    - x: Input data, of shape (N, C) where x[i, j] is the score for the jth
      class for the ith input.
    - y: Vector of labels, of shape (N,) where y[i] is the label for x[i] and
      0 <= y[i] < C

    Returns a tuple of:
    - loss: Scalar giving the loss
    - dx: Gradient of the loss with respect to x
    """
    loss, dx = None, None

    ###########################################################################
    # TODO: Copy over your solution from A1.
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    
    N, C = x.shape
    # 正确分类的得分
    correct_class_scores = x[range(N), y].reshape(N, 1)
    margins = np.maximum(0, x - correct_class_scores + 1)
    margins[range(N), y] = 0
    loss = np.sum(margins) / N

    margins[margins > 0] = 1
    margins[range(N), y] = -np.sum(margins, axis=1)
    dx = margins / N

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return loss, dx

​ 测试结果如下：

TwoLayerNet

​

init

​ __init__() 方法为 TwoLayerNet 的构造函数，主要用于初始化模型的参数。

def __init__(
    self,
    input_dim=3 * 32 * 32,
    hidden_dim=100,
    num_classes=10,
    weight_scale=1e-3,
    reg=0.0,
):
    """
    Initialize a new network.

    Inputs:
    - input_dim: An integer giving the size of the input
    - hidden_dim: An integer giving the size of the hidden layer
    - num_classes: An integer giving the number of classes to classify
    - weight_scale: Scalar giving the standard deviation for random
      initialization of the weights.
    - reg: Scalar giving L2 regularization strength.
    """
    self.params = {}
    self.reg = reg

    ############################################################################
    # TODO: Initialize the weights and biases of the two-layer net. Weights    #
    # should be initialized from a Gaussian centered at 0.0 with               #
    # standard deviation equal to weight_scale, and biases should be           #
    # initialized to zero. All weights and biases should be stored in the      #
    # dictionary self.params, with first layer weights                         #
    # and biases using the keys 'W1' and 'b1' and second layer                 #
    # weights and biases using the keys 'W2' and 'b2'.                         #
    ############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    self.params['W1'] = np.random.randn(input_dim, hidden_dim) * weight_scale
    self.params['b1'] = np.zeros(hidden_dim)
    self.params['W2'] = np.random.randn(hidden_dim, num_classes) * weight_scale
    self.params['b2'] = np.zeros(num_classes)

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ############################################################################
    #                             END OF YOUR CODE                             #
    ############################################################################

loss

​ loss 函数用于计算模型的损失以及损失相对于每个参数的梯度，梯度存放于 grads 字典中，键名与参数名对应。loss 函数就是执行模型的前向传播和反向传播两个部分，前向传播计算损失，反向传播计算损失相对于各参数的梯度，具体实现如下：

def loss(self, X, y=None):
    """
    Compute loss and gradient for a minibatch of data.

    Inputs:
    - X: Array of input data of shape (N, d_1, ..., d_k)
    - y: Array of labels, of shape (N,). y[i] gives the label for X[i].

    Returns:
    If y is None, then run a test-time forward pass of the model and return:
    - scores: Array of shape (N, C) giving classification scores, where
      scores[i, c] is the classification score for X[i] and class c.

    If y is not None, then run a training-time forward and backward pass and
    return a tuple of:
    - loss: Scalar value giving the loss
    - grads: Dictionary with the same keys as self.params, mapping parameter
      names to gradients of the loss with respect to those parameters.
    """
    scores = None
    ############################################################################
    # TODO: Implement the forward pass for the two-layer net, computing the    #
    # class scores for X and storing them in the scores variable.              #
    ############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    a, cache1 = affine_relu_forward(X, self.params['W1'], self.params['b1'])
    scores, cache2 = affine_forward(a, self.params['W2'], self.params['b2'])

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ############################################################################
    #                             END OF YOUR CODE                             #
    ############################################################################

    # If y is None then we are in test mode so just return scores
    if y is None:
        return scores

    loss, grads = 0, {}
    ############################################################################
    # TODO: Implement the backward pass for the two-layer net. Store the loss  #
    # in the loss variable and gradients in the grads dictionary. Compute data #
    # loss using softmax, and make sure that grads[k] holds the gradients for  #
    # self.params[k]. Don't forget to add L2 regularization!                   #
    #                                                                          #
    # NOTE: To ensure that your implementation matches ours and you pass the   #
    # automated tests, make sure that your L2 regularization includes a factor #
    # of 0.5 to simplify the expression for the gradient.                      #
    ############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    loss, dscores = softmax_loss(scores, y)
    # 加上 L2 正则化损失
    loss += 0.5 * self.reg * (np.sum(np.square(self.params['W1'])) + np.sum(np.square(self.params['W2'])))

    dx, grads['W2'], grads['b2'] = affine_backward(dscores, cache2)
    grads['W1'], grads['b1'] = affine_relu_backward(dx, cache1)[1:]

    # 梯度加上正则化项的梯度
    grads['W1'] += self.reg * self.params['W1']
    grads['W2'] += self.reg * self.params['W2']

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ############################################################################
    #                             END OF YOUR CODE                             #
    ############################################################################

    return loss, grads

​ 运行测试，测试结果如下：

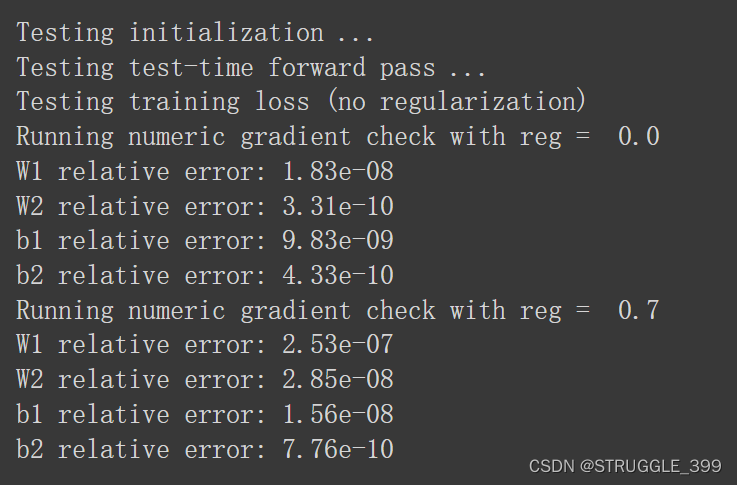
Solver

​ 作业一中提供了一个 Solver 工具类，用于模型的训练，Solver 类的构造函数中可以传递许多参数，其中必要的参数为 model 对象、训练数据 data，还有许多可选的参数，详情请见作业一的 cs231n/solver.py 文件。

input_size = 32 * 32 * 3
hidden_size = 50
num_classes = 10
model = TwoLayerNet(input_size, hidden_size, num_classes)
solver = None

##############################################################################
# TODO: Use a Solver instance to train a TwoLayerNet that achieves about 36% #
# accuracy on the validation set.                                            #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

solver = Solver(model, data, optim_config = {'learning_rate': 1e-3})
solver.train()

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
#                             END OF YOUR CODE                               #
##############################################################################

​ 测试结果如下，最终的验证精度达到了 50%：

​ 损失、训练精度/验证精度随着迭代次数（或epoch）的变化图如下。

​ 接下来将 TwoLayerNet 学习到的第一层权重进行可视化：

​ 权重可视化的结果如下：

​ 两层神经网络学习到的模板比线性分类器 softmax/svm 学习的模板更多，这里学习的模板数量为50个，因为隐藏层的大小/维度为50，上面的可视化结果就是这50个模板。

​ 最后的任务就是进行超参数调整(Hyperparameter tuning)了，我们在前面的学习率设定为固定学习率0.001时，模型已经获得50%的验证精度，在超参数调整过程中，发现当正则化参数大于10时，模型的训练精度、验证精度都下降的非常明显，说明模型发生欠拟合（Underfitting）。具体的超参数调整代码如下，

best_model = None

#################################################################################
# TODO: Tune hyperparameters using the validation set. Store your best trained  #
# model in best_model.                                                          #
#                                                                               #
# To help debug your network, it may help to use visualizations similar to the  #
# ones we used above; these visualizations will have significant qualitative    #
# differences from the ones we saw above for the poorly tuned network.          #
#                                                                               #
# Tweaking hyperparameters by hand can be fun, but you might find it useful to  #
# write code to sweep through possible combinations of hyperparameters          #
# automatically like we did on thexs previous exercises.                          #
#################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
best_val = -1
best_params = None

# learning_rates = [1e-4, 3e-4, 1e-3, 3e-3]
learning_rates = [1e-3, 2e-3]
regularization_strengths = [1e-3, 1e-2, 1e-1, 1, 1e1]

for lr in learning_rates:
  for reg in regularization_strengths:
    print('learing rate=%f, regularization strength=%f' % (lr, reg))
    model = TwoLayerNet(input_size, hidden_size, num_classes, reg=reg)
    solver = Solver(model, data, optim_config={'learning_rate': lr})
    solver.train()
    if solver.best_val_acc > best_val:
      best_val = solver.best_val_acc
      best_params = (lr, reg)
      best_model = model

    # visualize training loss and train / val accuracy
    plt.subplot(2, 1, 1)
    plt.title('Training loss(learing rate=%f, regularization strength=%f)' % (lr, reg))
    plt.plot(solver.loss_history, 'o')
    plt.xlabel('Iteration')

    plt.subplot(2, 1, 2)
    plt.title('Accuracy(learing rate=%f, regularization strength=%f)' % (lr, reg))
    plt.plot(solver.train_acc_history, '-o', label='train')
    plt.plot(solver.val_acc_history, '-o', label='val')
    plt.plot([0.5] * len(solver.val_acc_history), 'k--')
    plt.xlabel('Epoch')
    plt.legend(loc='lower right')
    plt.gcf().set_size_inches(15, 12)
    plt.show()


print('best validation accuracy achieved during cross-validation: %f' % best_val)
print('best learning rate=%f, best regularization strengths=%f' % best_params)

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
#                              END OF YOUR CODE                                #
################################################################################

​ 测试的结果如下，最终得到的最好的超参数组合为：(learning_rate, regularization_strength) = (0.001, 0.01)。最好的验证集精度为 51.7%。

best validation accuracy achieved during cross-validation: 0.517000
best learning rate=0.001000, best regularization strengths=0.010000

​ 最终模型在测试集中的准确率为 48.7%。

Inline Question 2

​ 现在您已经训练了一个神经网络分类器，但您可能会发现测试准确率远远低于训练准确率。我们可以通过哪些方法来缩小这一差距？请选所有适用的方法。

1. 在更大的数据集上进行训练。
2. 添加更多隐藏单元。
3. 增加正则化强度。
4. 以上都不是。

【答】1、3。

​ 测试准确率远远低于训练准确率表明神经网络发生了过拟合（Overfitting）。

1. 在更大的数据集上训练，一定程度上可以缓解过拟合现象。
2. 添加更多隐藏单元则会使得模型更深，更加复杂，更容易产生过拟合现象。
3. 增加正则化强度可以一定程度上使模型更简单，避免过拟合现象。

Q5: Higher Level Representations: Image Features

​ 我们已经看到，通过在输入图像的像素上训练线性分类器，我们可以在图像分类任务中取得合理的性能。在本练习中，我们将展示如何不根据原始像素，而是根据原始像素计算出的特征来训练线性分类器，从而提高分类性能。

# Use the validation set to tune the learning rate and regularization strength

from cs231n.classifiers.linear_classifier import LinearSVM

learning_rates = [1e-4, 3e-4, 1e-3, 3e-3, 1e-2, 3e-2]
regularization_strengths = [1e-6, 1e-5, 1e-4, 1e-3, 1e-2, 1e-1, 0, 1]

results = {}
best_val = -1
best_svm = None

################################################################################
# TODO:                                                                        #
# Use the validation set to set the learning rate and regularization strength. #
# This should be identical to the validation that you did for the SVM; save    #
# the best trained classifer in best_svm. You might also want to play          #
# with different numbers of bins in the color histogram. If you are careful    #
# you should be able to get accuracy of near 0.44 on the validation set.       #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

for lr in learning_rates:
  for reg in regularization_strengths:
    svm = LinearSVM()
    loss_hist = svm.train(X_train_feats, y_train, learning_rate=lr, reg=reg,
                      num_iters=1500, verbose=True)
    y_train_pred = svm.predict(X_train_feats)
    y_val_pred = svm.predict(X_val_feats)
    training_accuracy = np.mean(y_train == y_train_pred)
    validation_accuracy = np.mean(y_val == y_val_pred)
    results[(lr, reg)] = (training_accuracy, validation_accuracy)

    if best_val < validation_accuracy:
      best_val = validation_accuracy
      best_svm = svm
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# Print out results.
for lr, reg in sorted(results):
    train_accuracy, val_accuracy = results[(lr, reg)]
    print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
                lr, reg, train_accuracy, val_accuracy))

print('best validation accuracy achieved: %f' % best_val)

​ 测试结果如下：

lr 1.000000e-04 reg 0.000000e+00 train accuracy: 0.450694 val accuracy: 0.444000
lr 1.000000e-04 reg 1.000000e-06 train accuracy: 0.449633 val accuracy: 0.445000
lr 1.000000e-04 reg 1.000000e-05 train accuracy: 0.450959 val accuracy: 0.441000
lr 1.000000e-04 reg 1.000000e-04 train accuracy: 0.450837 val accuracy: 0.446000
lr 1.000000e-04 reg 1.000000e-03 train accuracy: 0.450714 val accuracy: 0.443000
lr 1.000000e-04 reg 1.000000e-02 train accuracy: 0.451980 val accuracy: 0.448000
lr 1.000000e-04 reg 1.000000e-01 train accuracy: 0.451429 val accuracy: 0.443000
lr 1.000000e-04 reg 1.000000e+00 train accuracy: 0.449531 val accuracy: 0.445000
lr 3.000000e-04 reg 0.000000e+00 train accuracy: 0.480020 val accuracy: 0.474000
lr 3.000000e-04 reg 1.000000e-06 train accuracy: 0.480102 val accuracy: 0.472000
lr 3.000000e-04 reg 1.000000e-05 train accuracy: 0.480245 val accuracy: 0.469000
lr 3.000000e-04 reg 1.000000e-04 train accuracy: 0.480102 val accuracy: 0.470000
lr 3.000000e-04 reg 1.000000e-03 train accuracy: 0.479490 val accuracy: 0.473000
lr 3.000000e-04 reg 1.000000e-02 train accuracy: 0.480490 val accuracy: 0.471000
lr 3.000000e-04 reg 1.000000e-01 train accuracy: 0.479531 val accuracy: 0.471000
lr 3.000000e-04 reg 1.000000e+00 train accuracy: 0.476939 val accuracy: 0.469000
lr 1.000000e-03 reg 0.000000e+00 train accuracy: 0.501408 val accuracy: 0.490000
lr 1.000000e-03 reg 1.000000e-06 train accuracy: 0.501204 val accuracy: 0.482000
lr 1.000000e-03 reg 1.000000e-05 train accuracy: 0.501776 val accuracy: 0.484000
lr 1.000000e-03 reg 1.000000e-04 train accuracy: 0.500939 val accuracy: 0.488000
lr 1.000000e-03 reg 1.000000e-03 train accuracy: 0.501633 val accuracy: 0.485000
lr 1.000000e-03 reg 1.000000e-02 train accuracy: 0.500510 val accuracy: 0.486000
lr 1.000000e-03 reg 1.000000e-01 train accuracy: 0.500367 val accuracy: 0.484000
lr 1.000000e-03 reg 1.000000e+00 train accuracy: 0.490245 val accuracy: 0.479000
lr 3.000000e-03 reg 0.000000e+00 train accuracy: 0.509510 val accuracy: 0.491000
lr 3.000000e-03 reg 1.000000e-06 train accuracy: 0.508755 val accuracy: 0.492000
lr 3.000000e-03 reg 1.000000e-05 train accuracy: 0.509816 val accuracy: 0.495000
lr 3.000000e-03 reg 1.000000e-04 train accuracy: 0.510449 val accuracy: 0.506000
lr 3.000000e-03 reg 1.000000e-03 train accuracy: 0.510816 val accuracy: 0.493000
lr 3.000000e-03 reg 1.000000e-02 train accuracy: 0.509673 val accuracy: 0.490000
lr 3.000000e-03 reg 1.000000e-01 train accuracy: 0.508286 val accuracy: 0.493000
lr 3.000000e-03 reg 1.000000e+00 train accuracy: 0.491898 val accuracy: 0.469000
lr 1.000000e-02 reg 0.000000e+00 train accuracy: 0.508510 val accuracy: 0.495000
lr 1.000000e-02 reg 1.000000e-06 train accuracy: 0.511102 val accuracy: 0.493000
lr 1.000000e-02 reg 1.000000e-05 train accuracy: 0.509061 val accuracy: 0.501000
lr 1.000000e-02 reg 1.000000e-04 train accuracy: 0.511857 val accuracy: 0.494000
lr 1.000000e-02 reg 1.000000e-03 train accuracy: 0.511347 val accuracy: 0.501000
lr 1.000000e-02 reg 1.000000e-02 train accuracy: 0.510429 val accuracy: 0.490000
lr 1.000000e-02 reg 1.000000e-01 train accuracy: 0.507592 val accuracy: 0.506000
lr 1.000000e-02 reg 1.000000e+00 train accuracy: 0.488551 val accuracy: 0.476000
lr 3.000000e-02 reg 0.000000e+00 train accuracy: 0.502694 val accuracy: 0.469000
lr 3.000000e-02 reg 1.000000e-06 train accuracy: 0.497265 val accuracy: 0.490000
lr 3.000000e-02 reg 1.000000e-05 train accuracy: 0.504612 val accuracy: 0.479000
lr 3.000000e-02 reg 1.000000e-04 train accuracy: 0.499633 val accuracy: 0.498000
lr 3.000000e-02 reg 1.000000e-03 train accuracy: 0.501592 val accuracy: 0.500000
lr 3.000000e-02 reg 1.000000e-02 train accuracy: 0.504776 val accuracy: 0.491000
lr 3.000000e-02 reg 1.000000e-01 train accuracy: 0.497673 val accuracy: 0.470000
lr 3.000000e-02 reg 1.000000e+00 train accuracy: 0.471184 val accuracy: 0.447000
best validation accuracy achieved: 0.506000

​ 在测试集的测试精度为 48.5%。

Inline Question 1

​ 下面输出的是一些分类错误的案例，描述你看到的错误分类结果，它们有意义吗？

接下来使用两层神经网络基于图像特征进行超参数调整：

from cs231n.classifiers.fc_net import TwoLayerNet
from cs231n.solver import Solver

input_dim = X_train_feats.shape[1]
hidden_dim = 500
num_classes = 10

data = {
    'X_train': X_train_feats,
    'y_train': y_train,
    'X_val': X_val_feats,
    'y_val': y_val,
    'X_test': X_test_feats,
    'y_test': y_test,
}

net = TwoLayerNet(input_dim, hidden_dim, num_classes)
best_net = None

################################################################################
# TODO: Train a two-layer neural network on image features. You may want to    #
# cross-validate various parameters as in previous sections. Store your best   #
# model in the best_net variable.                                              #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

best_val = -1
learning_rates = [1e-4, 3e-4, 1e-3, 3e-3, 1e-2, 3e-2, 1e-1]
regularization_strengths = [1e-6, 1e-5, 1e-4, 1e-3, 1e-2, 1e-1, 0, 1]

for lr in learning_rates:
  for reg in regularization_strengths:
    print('learning rate=%f, regularization strength=%f' % (lr, reg))
    net = TwoLayerNet(input_dim, hidden_dim, num_classes, reg=reg)
    solver = Solver(net, data, optim_config={'learning_rate': lr}, num_epochs=10)
    solver.train()
    if best_val < solver.best_val_acc:
      best_net = net
      best_val = solver.best_val_acc
      best_params = (lr, reg)

print('best learning rate=%f, best regularization strength=%f' % best_params)
print('best validation accuracy achieved: %f' % best_val)

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

​ 最终得到的最好验证精度为 61.1%，对应的超参数组合为：learing rate, regularization strength= (0.100000, 0.000001)：

best learning rate=0.100000, best regularization strength=0.000001
best validation accuracy achieved: 0.611000

最终得到的验证精度为 58.9%