图神经网络task6

基于图神经网络的图表征学习方法

DIFFPOOL

DIFFPOOL 允许开发可以学习在图的层级表征上运行的更深度的 GNN 模型。他们开发了一个和 CNN 中的空间池化操作相似的变体，空间池化可以让深度 CNN 在一张表征越来越粗糙的图上迭代运行。与标准 CNN 相比，GNN 的挑战在于图不包含空间局部性的自然概念，也就是说，不能将所有节点简单地以「m*m 补丁」的方式池化在一张图上，因为图复杂的拓扑结构排除了任何直接、决定性的「补丁」的定义。此外，与图像数据不同，图形数据集中包含的图形节点数和边数都不同，这使得定义通用的图形池化操作符更具挑战性。

为了解决上述问题，我们需要一个可以学习如何聚合节点以在底层图形上建立层级多层支架的模型。DIFFPOOL 在深度 GNN 的每一层学习了可微分的软分配，基于学习到的嵌入，将节点映射为一组聚类。以该方法为框架，我们通过分层的方式「堆叠」了 GNN 层建立了深度 GNN（图 1）：GNN 模块中 l 层的输入节点对应 GNN 模块中 1 层（1 个 GNN 模块）学到的簇。因此，DIFFPOOL 的每一层都能使图形越来越粗糙，然后训练后的 DIFFPOOL 就可以产生任何输入图形的层级表征。本研究展示了 DIFFPOOL 可以结合到不同的 GNN 方法中，这使准确率平均提高了 7%，并且在五个基准图形分类任务中，有四个达到了当前最佳水平。最后，DIFFPOOL 可以学习到与输入图中明确定义的集合相对应的可解释的层级簇。

GraphSAGE

GraphSAINT 提出了一种通用的概率图采样器，通过对原始图的采样子图来构造训练批次。图采样器可以根据不同的方案设计：例如，它可以执行均匀节点采样、均匀边采样，或者通过使用随机漫步来计算节点的重要性，并将其作为采样的概率分布，进行“重要性”采样。
同样重要的是要注意到，采样的优势之一是在训练过程中，它可以作为一种边级 Dropout，这可以使模型规范化，并有助于提高性能。然而，边 Dropout 需要在推理时仍能看到所有的边，这在这里是不可行的。图采样可能产生的另一个效果是减少瓶颈，以及由此产生的“过度挤压”现象，这种现象源于邻域的指数扩展。

通过将不同的、固定的邻域聚合器结合在一个卷积层中，可以获得一个极易扩展的模型，而不需要借助图采样。换句话说，所有与图相关的（固定的）操作都在架构的第一层，因此可以进行预计算；然后可以将预聚合的信息作为输入馈送到模型的其余部分，由于缺乏邻域聚合，该模型归结为多层感知器（Multi-layer perceptron，MLP）。重要的是，即使采用这样一个浅卷积方案，通过采用几个可能是专门的、更复杂的扩散操作符，仍然可以保留图过滤操作的表达力

SIGN 的主要优点在于它的可扩展性和效率，因为它可以使用标准的小批次梯度下降法进行训练。我们发现，我们的模型在推理时比 ClusterGCN 和 GraphSAINT 快了两个数量级，而且在训练时也快得多（所有这些都保持了正确率与非最先进的 GraphSAINT 接近）

6号、3号和5号节点的从1层到3层到WL子树。

Graph Isomorphism Network (GIN) 图同构网络

为了研究GNN的表示能力，可以分析GNN将两个节点映射到embedding空间的同一位置时的表示能力，所以可以将分析简化为这样一个问题:GNN是否可以将不同的图结构映射(即两个multisets)到相同的embedding。这种将任意两个不同的图映射到不同embedding的能力意味着要解决具有挑战性的图同构问题。也就是说，希望同构图的embedding相同，非同构图的embedding不同。一个强大的GNN不会将两个不同的邻域映射到相同的表示，这意味着它的聚合模式必须是单射的（injective）

MLP可以近似拟合任意函数，故可以学习到单射函数，而graphsage和gcn中使用的单层感知机不能满足。
约束输入特征是one-hot，故第一次迭代sum后还是满足单射性，不需先做MLP的预处理。
根据定理4， 迭代一轮得到新特征是可数的、经过了 转换f(x)（隐），下一轮迭代还是满足单射性条件。

诸多 GNN 变体没有 GIN 能力强，其实是 GNN 变体不满足单射的原因。

首先，大部分 GNN 变体的层数都比较少，大部分都只有一层。单层感知机的行为就像是线性映射，此时 GNN 层对退化为简单的对领域特征求和。虽然我们可以证明在有偏执项和足够多的输出维度的情况下，单层感知机是可以完成多重集的单射的，但这种映射无法捕获图结构的相似性。并且对于单层感知机来说，有时会出现数据拟合严重不足的情况，其拟合能力无法与 MLP 相提并论，并且在测试精度上往往比具有 MLP 的 GNN 表现更差。

GIN用于图分类，在理论上就是有局限的，WLS填补了这个局限

简单来讲：主要是围绕单射函数这个点来证明WLS填补了局限，WL算法可以保证是单射函数。

如果函数是单射函数，则可以保证图神经网络的强幂
GIN 架构提出的替代方案是用 MLP 替换单射函数 ，并且由于通用近似定理（universal approximation theorem），我们知道，MLP 可以近似任何函数，包括单射函数。因此，具体地说，GIN 的嵌入更新具有以下形式：

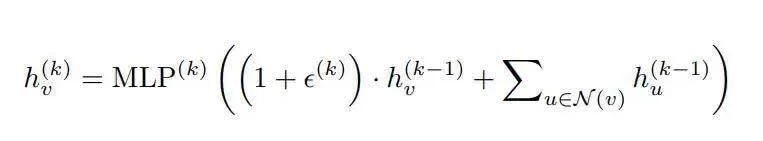
MLP 内部的东西并不能保证是单射的，而且 MLP 本身也不能保证是单射的。事实上，对于第一层，如果输入特征是独热编码（one-hot encode），那么 MLP 内部的和将是单射的，原则上，MLP 可以学习单射函数。但是在第二层及后面的层，节点嵌入变得不合理

在训练中并没有任何东西可以保证这种单射性，而且可能还会有一些图是 GIN 无法区分的，但 WL 可以。所以这是对 GIN 的一个很强的假设，如果违反了这一假设，那么 GIN 的性能将受到限制。

引用

链接: datawhale-gnn
链接: 图神经网络+池化模块
链接: 简单且可扩展的图神经网络
链接: GIN 图同构网络 ICLR 2019 论文详解
链接: WL-test：GNN 的性能上界
链接: 浅谈图神经网络的局限性