数据结构与算法python—1.数据结构与算法入门

1.算法与数据结构的引入

1.1 算法的引入

  如果 $a+b+c=1000$，且 $a^2+b^2=c^2$（a,b,c 为自然数），如何求出所有a、b、c可能的组合?
第一次尝试

#枚举法
import time
start = time.time()
#三重循环
for a in range(1001):
    for b in range(1001):
        for c in range(1001):
            if a+b+c ==1000 and a**2+b**2 == c**2:
                print("a,b,c:%d,%d,%d"%(a,b,c))
end = time.time()
print("*********")
print("总共运行了{}秒".format(end-start))
>>>
a,b,c:0,500,500
a,b,c:200,375,425
a,b,c:375,200,425
a,b,c:500,0,500
*********
总共运行了107.92784237861633秒

第二次尝试：优化

#代码优化
import time
start = time.time()
#二重循环
for a in range(1001):
    for b in range(1001):
        c = 1000 -a-b
        if a**2+b**2 == c**2:
            print("a,b,c:%d,%d,%d"%(a,b,c))
end = time.time()
print("*********")
print("总共运行了{}秒".format(end-start))
>>>
a,b,c:0,500,500
a,b,c:200,375,425
a,b,c:375,200,425
a,b,c:500,0,500
*********
总共运行了1.0254335403442383秒

1.2 数据结构的引入

  相互之间存在一种或者多种特定关系元素的数据元素的集合被称为数据结构。数据结构可以从逻辑结构与物理结构两个方面来介绍
逻辑结构：数据对象中数据元素之间的相互关系
逻辑结构是面向问题的

1. 集合结构
   集合结构中的数据元素除了同属一个集合之外，他们之间没有其他的关系
2. 线性结构
   线性结构中数据元素是一对一的关系
   
3. 树形结构
   树形结构中的数据元素存在一对多的关系
   
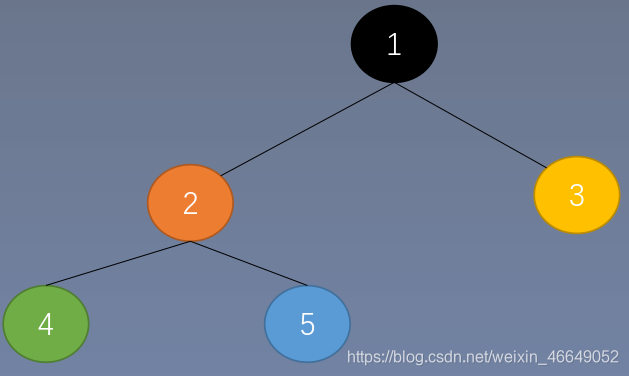
4. 图形结构
   图形结构中的数据元素是多对多的关系
   

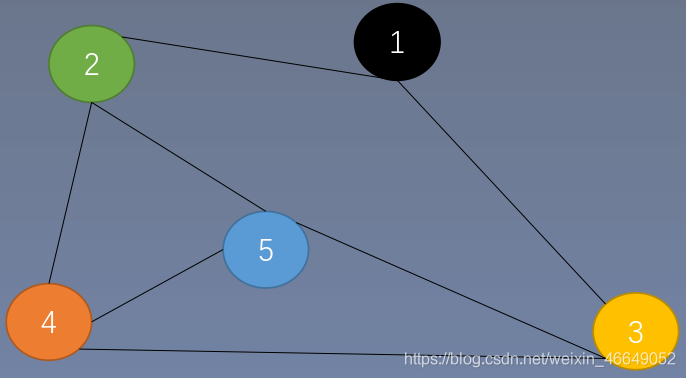
物理结构：数据的逻辑结构在计算机中的存储形式
物理结构是面向计算机的

1. 顺序存储
   把数据元素存放在地址连续的存储单元里，其数据间的逻辑关系和物理关系是一致的
   
2. 链式存储
   把数据元素存放在任意的存储单元里面，这组存储单元可以是连续的,也可以是不连续的
   

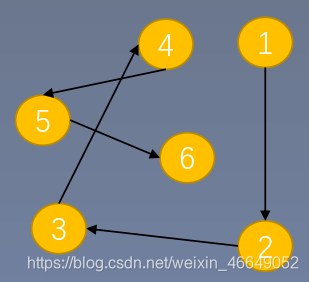
2.算法的提出

2.1 算法的概念

  算法是计算机处理信息的本质，因为计算机程序本质上是一个算法来告诉计算机确切的步骤来执行一个指定的任务。算法是解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作。

2.2 算法五大特性

1. 输入: 算法具有0个或多个输入
2. 输出: 算法至少有1个或多个输出
3. 有穷性: 算法在有限的步骤之后会自动结束而不会无限循环，并且每一个步骤可以在可接受的时间内完成
4. 确定性：算法中的每一步都有确定的含义，不会出现二义性
5. 可行性：算法的每一步都是可行的，也就是说每一步都能够执行有限的次数完成

2.3 算法设计的要求

1. 正确性:算法的正确性是指算法至少应该具有输入、输出和加工处理无歧义性、能反映问题的需求，能够得到问题的答案
2. 可读性:算法设计的另一目的就是为了便于阅读、理解和交流
3. 健壮性:当输入数据不合法时，算法也能做出相关处理

时间效率高和存储量低

3.算法效率衡量

  假定计算机执行算法每一个基本操作的时间是固定的一个时间单位，那么有多少个基本操作就代表会花费多少时间单位。虽然对于不同的机器环境而言，确切的单位时间是不同的，但是对于算法进行多少个基本操作（即花费多少时间单位）在规模数量级上却是相同的，由此可以忽略机器环境的影响而客观的反应算法的时间效率。

3.1 大O计法

  大O记法：对于单调的整数函数f，如果存在一个整数函数g和实常数c>0，使得对于充分大的n总有$f(n)<=c\ast g(n)$，就说函数g是f的一个渐近函数（忽略常数），记为f(n)=O(g(n))。也就是说，在趋向无穷的极限意义下，函数f的增长速度受到函数g的约束，亦即函数f与函数g的特征相似
理解大O算法：对于算法的时间性质和空间性质，最重要的是其数量级和趋势，这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。大O算法描述的是算法运行时间和输入数据规模之间的关系。

3.2 时间复杂度

  时间复杂度：假设存在函数g，使得算法A处理规模为n的问题示例所用时间为T(n)=O(g(n))，则称O(g(n))为算法A的渐近时间复杂度，简称时间复杂度，记为T(n)

3.2.1 最坏时间复杂度

  最坏时间复杂度：对于最坏时间复杂度，提供了一种保证，表明算法在此种程度的基本操作中一定能完成工作。这是我们主要关注的。

算法完成工作最少需要多少基本操作，即最优时间复杂度
算法完成工作最多需要多少基本操作，即最坏时间复杂度
算法完成工作平均需要多少基本操作，即平均时间复杂度

3.2.2时间复杂度的几条基本运算规则

1. 基本操作，即只有常数项，认为其时间复杂度为O(1)
2. 顺序结构，时间复杂度按加法进行计算
3. 循环结构，时间复杂度按乘法进行计算
4. 分支结构，时间复杂度取最大值
5. 判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略
6. 在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度

如何分析一个算法的时间复杂度？
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

接下来通过例子来理解时间复杂度的基本运算规则

for a in range(0, 1001):
    for b in range(0, 1001):
        for c in range(0, 1001):
            if a**2 + b**2 == c**2 and a+b+c == 1000:
                print("a, b, c: %d, %d, %d" % (a, b, c))
#时间复杂度
T(n) = n*n*n*(max(0,1))
	 =O(n^3)

for a in range(1001):		#循环结构
    for b in range(1001):	#循环结构
        c = 1000 -a-b		#顺序结构
        if a**2+b**2 == c**2:#分支结构
            print("a,b,c:%d,%d,%d"%(a,b,c))
#时间复杂度
T(n) = n * n*(1+max(0,1))
     =n^2*2
     =O(n**2)

count = 1
while count < n:
	count *= 2
# 时间复杂度
T(n) = O(log_2(n))
	 = O(log(n))

for i in range(n):
	for j in range(i,n):

# 时间复杂度相当于从1到n相加
T(n) = O(n(n+1)/2) = O(n^2)

3.2.3 常见时间复杂度

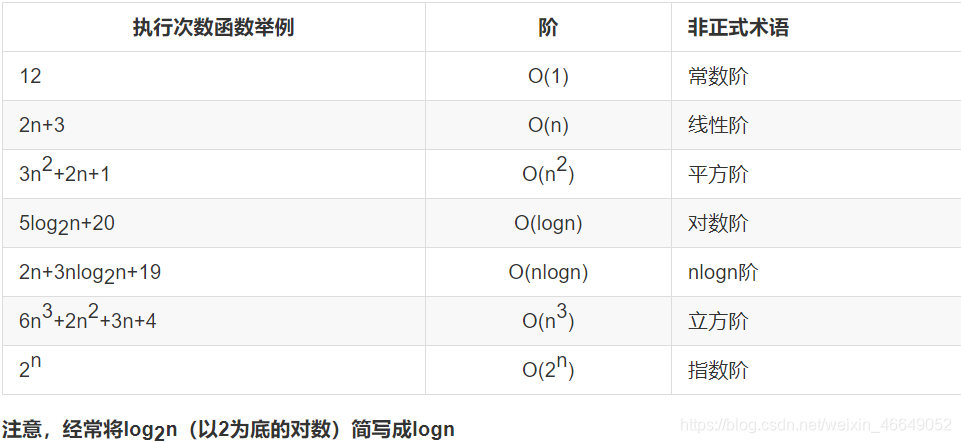
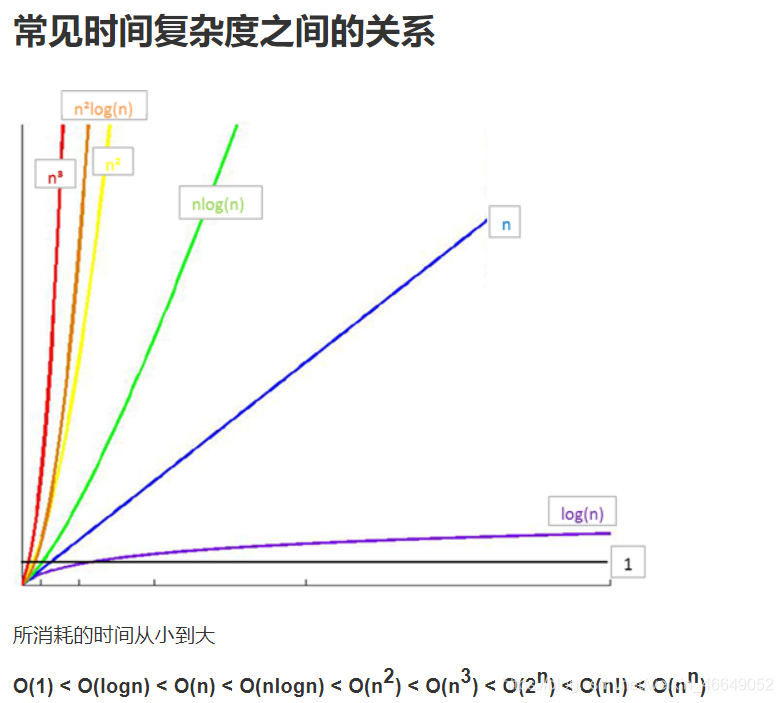
4.python内置类型性能分析

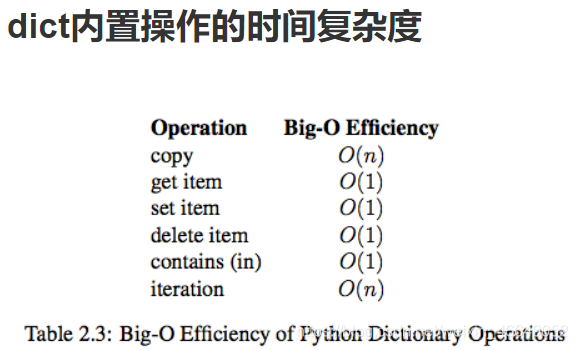
列表的索引操作是O(1)
字典的读取与赋值操作是O(1)

4.1 timeit模块

timeit模块可以用来测试一小段Python代码的执行速度。

class timeit.Timer(stmt='pass', setup='pass', timer=<timer function>)

# Timer是测量小段代码执行速度的类。
# stmt参数是要测试的代码语句（statment）；
# setup参数是运行代码时需要的设置；
# timer参数是一个定时器函数，与平台有关。

timeit.Timer.timeit(number=1000000)

Timer类中测试语句执行速度的对象方法。number参数是测试代码时的测试次数，默认为1000000次。方法返回执行代码的平均耗时，一个float类型的秒数。

4.2 list性能操作测试

def t1():
   l = []
   for i in range(1000):
      l = l + [i]
def t2():
   l = []
   for i in range(1000):
      l.append(i)
def t3():
   l = [i for i in range(1000)]
def t4():
   l = list(range(1000))


from timeit import Timer

t_1 = Timer("t1()", "from __main__ import t1")        #__main__表示调用当前模块的方法
print("concat ",t_1.timeit(number=1000), "seconds")
t_2 = Timer("t2()", "from __main__ import t2")
print("append ",t_2.timeit(number=1000), "seconds")
t_3 = Timer("t3()", "from __main__ import t3")
print("comprehension ",t_3.timeit(number=1000), "seconds")
t_4 = Timer("t4()", "from __main__ import t4")
print("list range ",t_4.timeit(number=1000), "seconds")
>>>
concat  1.0260217 seconds
append  0.050984700000000105 seconds
comprehension  0.026266700000000087 seconds
list range  0.01072889999999993 seconds

5.数据结构

5.1 概念

  数据是一个抽象的概念，将其进行分类后得到程序设计语言中的基本类型。如：int，float，char等。数据元素之间不是独立的，存在特定的关系，这些关系便是结构。数据结构指数据对象中数据元素之间的关系。
  为了解决问题，需要将数据保存下来，然后根据数据的存储方式来设计算法实现进行处理，那么数据的存储方式不同就会导致需要不同的算法进行处理。Python给我们提供了很多现成的数据结构类型，这些系统自己定义好的，不需要我们自己去定义的数据结构叫做Python的内置数据结构，比如列表、元组、字典。而有些数据组织方式，Python系统里面没有直接定义，需要我们自己去定义实现这些数据的组织方式，这些数据组织方式称之为Python的扩展数据结构，比如栈，队列等。

5.2 算法与数据结构的区别

数据结构只是静态的描述了数据元素之间的关系。
高效的程序需要在数据结构的基础上设计和选择算法。
程序 = 数据结构 + 算法
总结：算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体

5.3 抽象数据类型

  抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起，进行封装。引入抽象数据类型的目的是把数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开，使它们相互独立。

最常用的数据运算有五种：

1. 插入
2. 删除
3. 修改
4. 查找
5. 排序

---

如果对您有帮助，麻烦点赞关注，这真的对我很重要！！！如果需要互关，请评论或者私信！

---