A/Btest测试分析

一、首页是否改版

• 背景：APP首页是否应该添加菜谱推荐来引导消费者进一步购买相应食材
• 随机的将人群划分为A实验组和B对照组
• A实验组人群采用添加菜谱推荐的APP
• B对照组人群依旧采用之前的APP

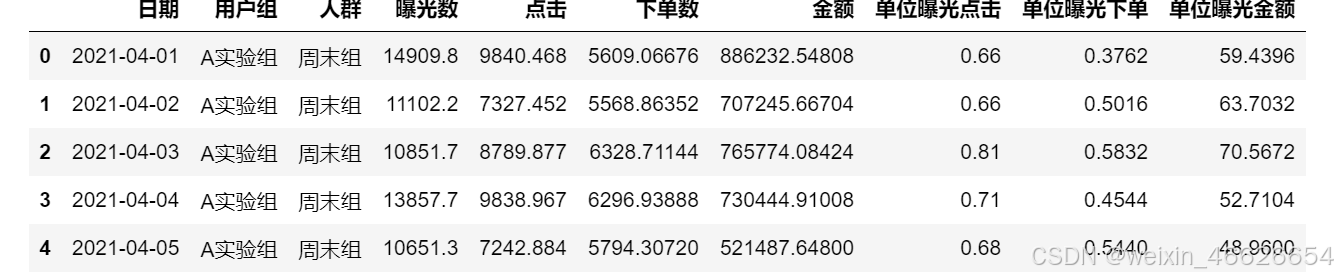
表中的变量说明

• 日期：客户下单日期
• 用户组：包括A实验组，B对照组
• 人群：周末组，工作日组（喜欢周末逛APP的和喜欢工作日逛app的）
• 曝光数：该日进入APP的人数
• 点击：该日查看商品的人数
• 下单数：该日下单的人数
• 金额：该日下单支付的金额
• 单位曝光点击：点击人数/总人数
• 单位曝光下单：下单数/总人数
• 单位曝光金额：金额/人数

分析思路

• 1.数据的清洗
• 2.客户的流失率
• 3.A/Btest检验

import numpy as np
import pandas as pd
import scipy.stats as stats #Scipy 模块，这个模块专门运用于统计和优化技术
import matplotlib.pyplot as plt
import seaborn as sns #可视化库

#导入数据：
df=pd.read_excel(r'D:\日常文档\笔记\泰坦尼克号数据\ABtest/abtest.xlsx')
df.head()

# 数据的清洗¶
#查看数据是否有空值，以及各变量的类型
df.info()
#查看重复值个数
df.duplicated().sum()
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False

#列变行用户组    人群    曝光数    点击    下单数    
# pd.melt列转行。
data1 = pd.melt(df,id_vars=['用户组'],value_vars=['曝光数','点击','下单数'],var_name='阶段',value_name='数量')
data1.head()

fun = data1.groupby(by=['用户组','阶段']).sum()
fun = fun.reset_index()
fun.sort_values(by=['用户组','数量'],ascending=False,inplace=True)
fun.head(6)

 import plotly.express as px # plotly.express 的漏斗图
fig = px.funnel(fun, x='数量', y='阶段', color='用户组')
fig.show()

def apply_fanc(x):
    perent = x.数量/np.sum(x.数量)
    return perent
a1 = fun.groupby('用户组').apply(apply_fanc)
a1.index = [1,2,0,4,5,3]
b = fun.copy()
b['占比']=a1
b
fig = px.funnel(b, x='占比', y='阶段', color='用户组')
fig.show()

# 初步判断A实验组和B对照组的各阶段人数几乎相同，各阶段客户留存也无较大差异，可初步确定前后无差异

# 2.进行检验
df.head()
# 经上述查看，前后APP下单数量以及其他没有什么太大的区别，最后查看金额是否有区别

df.groupby('用户组')['金额'].sum()

# 初步查看出，变换后的金额明显增加，而且下单量较小，APP首页添加菜谱推荐可以更好的来引导消费者进一步购买相应食材
# 为避免数量级对实验的影响，采用单位曝光金额进行检验

# 假设判断：H0：变换页面后有明显的改变

# 选择统计量：
df.用户组.value_counts()

# 方法一：大样本，总体方差未知，样本方差不同，采用独立样本异方差t检验
df.groupby('用户组').agg({'单位曝光金额':np.var})


# 方法二：P值小于0.05，则数据不具有方差齐性，需要加上参数equal_val并设定为False。
data1=df[df.用户组=="A实验组"]["单位曝光金额"]
data=df[df.用户组=="B 对照组"]["单位曝光金额"]
stats.levene (data1,data)

a1 = df[df['用户组']=='A实验组'].单位曝光金额
a2= df[df['用户组']=='B 对照组'].单位曝光金额
from scipy import stats

t,p = stats.ttest_ind(a1, a2,axis=0,equal_var = False)
# print('t双侧检验 = {}'.format(t))
# print('P（T<=t）= {}'.format(p))
t,p
# 由于P（T<=t）= 0.03574319626560325 >0.025 ,不能拒绝原假设

# 假设 H0：a1<=a2 H1:a1>a2  统计者想要拒绝的假设放在原假设
t,p = stats.ttest_ind(a1, a2,axis=0,equal_var =False,alternative='greater')
print('t单侧检验 = {}'.format(t))
print('P（T<=t）= {}'.format(p))
# 由于P（T<=t）= 0.017871598132801626<0.05 ,拒绝原假设
# 即：实验组的均值大于对照组
# APP首页添加菜谱推荐可以更好的来引导消费者进一步购买相应食材

# t.test(y ~ x, data) 可以添加一个参数
# alternative="less"或alternative="greater"来进行有方向的检验。（单侧或双侧）
# 如果数据无法满足t检验或ANOVA的参数假设，可以转而使用非参数方法。举例来说，若结
果变量在本质上就严重偏倚或呈现有序关系， 则我们就要召唤另一个神器出来,样本量较小,非参数检验，例如曼-惠特尼 U 测试（Mann-Whitney U test），它不依赖于数据的分布假设。
# 若两组数据独立，可以使用Wilcoxon秩和检验（更广为人知的名字是Mann-Whitney U检验）
u_stat, p_value_mannwhitney = stats.mannwhitneyu(
    df[df['Page'] == 'Page A']['Time'],  # 选择页面A的数据
    df[df['Page'] == 'Page B']['Time'],  # 选择页面B的数据
    alternative='two-sided'  # 双侧检验，检查中位数是否相等
)
u_stat, p_value_mannwhitney