【算法】动态规划——将问题转化为小问题

目录

1. 背包问题

1.1 简单算法

1.2 动态规划

2. 背包问题FAQ

2.1 再增加一件商品将如何呢？

2.2 行的排列顺序发生变化时结果将如何？

2.3 可以逐行而不是逐列填充网格吗？

2.4 增加一件更小的商品将如何呢？

2.5 可以偷商品的一部分吗？

2.6 旅游行程最优化

2.7 处理相互依赖的情况

2.8 计算最终的解时会涉及两个以上的子背包吗？

2.9 最优解可能导致背包未装满吗？

3. 最长公共子串

3.1 绘制网络

3.2 填充网格

3.3 最长公共子序列

3.4 动态规划的应用

4. 总结

---

1. 背包问题

假设你是个小偷，背着一个可装4磅重东西的背包。你可以盗窃的商品有如下三件。为了让盗窃的撒谎给你品价值最高，你该选择哪些商品？

1.1 简单算法

最简单的算法如下：尝试各种可能的商品组合，并找出价值最高的组合。

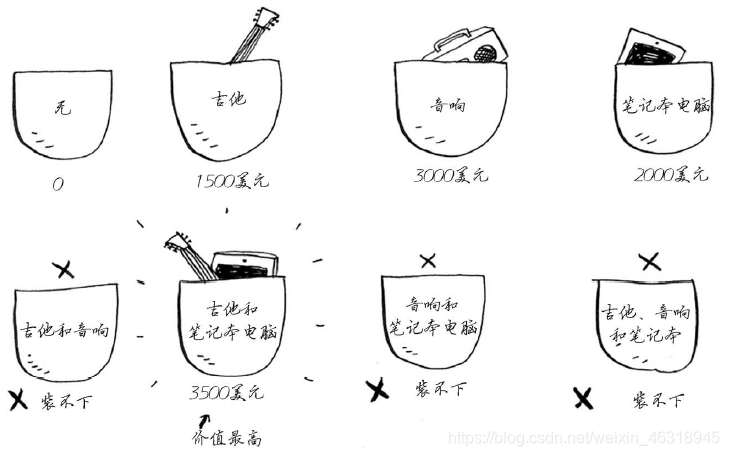
这样可行，但速度非常慢。在有3件商品的情况下，你需要计算8个不同的集合；有4件商品时，你需要计算16个集合。每增加一件商品，需要计算的集合数都将  ！这种算法的运行时间为O(2ⁿ)，真的是慢如蜗牛。