置换的轮换表示

问题描述

给出一个置换，写出该置换的轮换表示。比如

表示为(1 3 6 7 8 4 2)(5 9)

输入：置换后的序列
输出：不相杂的轮换乘积，每行表示一个轮换（轮换的起始数字最小，每个轮换的起始数字递增排序，单轮换省略）

知识回顾

置换的轮换表示

不相杂轮换

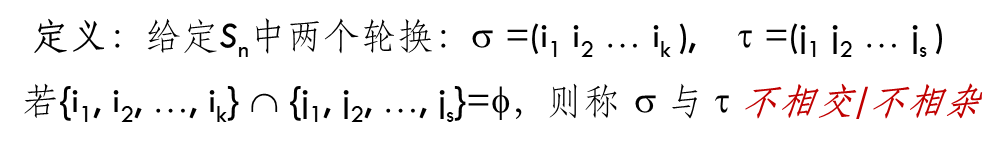
题目解读

这道题默认置换前是（1 2 3…）,具体有几个数在测试用例输入之前谁也不知道。输入的测试用例是一串数字，这一串数字用空格分隔，是（1 2 3…）的一个置换之后的序列，输入之后也就确定了这映射是从哪个集合到其自身的置换。置换已经确定，由上述定理知道上述定理置换可以转换成一组不相交的轮换，不过这些轮换每个有几个数字一共有几组也不能事先确定。题目要求我们输出的是每一个轮换为一行，轮换内部按空格分隔，我们事前并不知道也无法通过计算得知输出有几行，每行有几个数字。但是我们能确定的是 这一组轮换最大长度 是和置换长度相等的。

编程实现

• 输入置换后的数组
• 构建置换（映射）
• 循环，每次循环保存一个轮换
  • 首先确定当前轮换的首元素
  • 如果首元素不是0 ，顺藤摸瓜找下一个元素
    • 如果下一个元素不等于首元素，继续查找，并把当前元素保存到result数组中
    • 如果下一个元素等于首元素，已经找到一个完整的轮换，记录此时result数组索引值，本轮循环退出，进行下一次循环找下一个轮换
  • 如果首元素是0，说明所有的轮换都被找到
• 输出，通过检测每个轮换的在result数组索引起始位置和结束位置，来输出（如果结束位置-起始位置=1，意味着是单轮换，不输出）

#include <stdio.h> 
#include <string.h>

# define MAXSIZE 10 


int Find(int *arr, int len, int x) {
	/*
	:参数 arr: 数组名
    :参数 len: 数组长度 
    :参数 x: 待查找元素 
    :return: 存在返回1 不存在返回0 
	*/
	int i; 
	for(i=0; i < len; i++){
		if(arr[i] == x){
			return 1; 
		}
	}
	return 0;
}

int main()
{
	/*--------输入数据--------*/
	int values[MAXSIZE];
	char str[2*MAXSIZE];
	gets(str);
	int totallength = strlen(str);
	int length = (totallength+1)/2;
	int i;
	for (i=0; i<length; i++){
		values[i] = str[2*i] -48;
	}
	//cout << "length:" << length<< endl;
	
	/*--------构造映射--------*/
	int f[MAXSIZE+1] = {0}; 
	int j;
	for(j = 0; j < length; j++){	
		f[j+1] = values[j];
	}
	
	int result[MAXSIZE]={0}; //保存轮换
	int index[MAXSIZE] ={0}; //分割两个轮换的索引值
	int count = 0;  
	int pos = 0;
	
	while(1) {
		int i;
		//cout << "第" << count << "轮..." << endl; 
		int first = 0;
		for(i=1; i<=length; ++i) {
			if(Find(result,length,i)==0){
				first = i;
				break;
			}
		}
		//cout << "first: " << first << endl;
		if(first==0) { //所有轮换都已经找到，退出 
			break;
		}
		
		//初始化轮换当前元素和下一个元素
		int current_item = first;
		int next_item = f[current_item];
		
		while(1) {
			// 当前元素插入当前轮换尾部 
			result[pos] = current_item;
			pos++;
			if(next_item != first) {
				current_item = next_item;
            	next_item = f[current_item];
			}
			else {
				// 这次轮换共有几个数存入索引数组 以便输出 
            	index[count] = pos;
            	break;
			}
		}
		count += 1;
	}
	
	
	int m,n,k = 0;
	
	/*---确定结果有几个不相杂轮换---*/ 
	for(m=0; m<MAXSIZE; m++){
		if(index[m]==0)
			break;
	}
	
	/*-----每个轮换一行输出-----*/
	for(n=0;n<m;n++){
		if(index[n]-k == 1)
			continue;
		for(k=k;k<index[n];k++) {
			printf("%d ", result[k]);
		}
		printf("\n");
	}
	
	return 0;
} 

• 测试用例1：
  

• 测试用例2：
  

• 测试用例3：