逻辑斯蒂回归 matlab实现

说明

我将试图从感知机的基础上说明逻辑回归的一般性原理和学习及预测方法，其中缺少一些必要的证明，包括了一个二分类问题的实例。其中关于感知机的实验在 机器学习 专栏中有介绍。

从感知机到逻辑斯蒂回归

感知机模型：

·应用范围：

二分类问题，线性分类模型，属于判别模型

·输入输出：

In: n维的特征空间X
Out: y={+1,-1}，即类别的label

·关系:

f(x) = sign(w·x + b)
其中：·sign(x)为符号函数
·w·x + b = 0：
对应n维特征空间中的一个超平面,w对应法向量，b为截距。若选取合适，这个超平面将会把所有实例（x,y）分为两类。
·训练集：表示为T{(x1,y1),(x2,y2)…}；
·判别：若数据集线性可分，则一定存在一超平面w·x + b = 0；对所有yi = 1的实例，都有w·x + b>0,对所有yi = -1的实例，都有w·x + b<0。由此通过一个“外壳” sign函数，即可进行有效分类。

·学习策略：

·Lossfunction:
·注意：选取损失函数时要保证损失函数是参数的连续可导函数，这样便于优化。可以引入误分类点到超平面的总距离这一概念，将其作为损失函数。误分类点数越少，超平面越接近“理想答案”，损失函数越小，这一思路是直观和易于接受的。
·关于距离，引入了范数的概念，并且对比函数间距 |w·x0 + b| 以及几何间距|w·x0 + b|/||w||，机器学习中常用后者，即几何间距，这样的损失函数对比例是鲁棒的。如果采用函数间距，缺陷比较明显，学习到的参数较小。误分类点到超平面S的距离为：（即高中几何距离算法）-yi(w·xi + b)/||w||
·如何选取误分类点:对于被正确分类的点，有yi·（w·x0 + b）> 0,相应的误分类点就有yi·（w·x0 + b）< 0；
·损失函数表达式:L(w,b) = -Σyi·(w·xi + b) (（xi，yi）为误分类点)
参数更新：
·梯度：用损失函数分别对w，b求导，得到梯度

·参数更新：
w <———— w + μ·yi·xi
b <———— b + μ·yi

·算法描述：

输入：
训练数据集T = {(x1,y1),(x2,y2),(x3,y3),…… },xi为n维特征空间的特征向量，yiϵ{+1,-1},i = 1,2……学习率μ(0≤μ≤1)
输出：
w,b，以及感知机模型为f(x) = sign(w·x + b);
(1) 设定w,b初始值
(2) 训练集中选取数据(xi,yi)
(3) 判断如果yi·(wi·x + b) ≤0,则更新参数
w <———— w + μ·yi·xi
b <———— b + μ·yi
(4) 转至(2)直到没有误分类点

·实验结果：

Matlab完成了感知机算法，随着训练集数据的增多，发现出现了不能找到超平面的情况，此时将学习率调低，随之又找到了合适的参数，单同时由于学习率较低，使得学习到的参数很小。
事实上，感知机存在着一个很大的弊端，即它敏感的“非黑即白”式的判断结果未免太过武断，事实上对于很多分类问题两个相距很近的点可能并没有如此之大的差距，为了使得更加细致的描绘这种点和点之间的差距，引入了逻辑斯蒂回归。

逻辑斯蒂回归模型：

·适用范围：

分类问题，二分类甚至是多分类。属于对数线性模型（输出Y=1的对数概率是输入的线性函数）

·输入输出：

In: T = { (xi,yi) | i = 1,2,3,…},xi为n维特征空间中的特征向量。Yi∈{+1，-1}
Out:逻辑斯蒂回归模型

·函数关系：

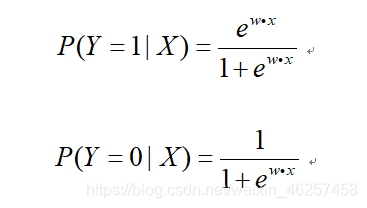
另外，定义了事件几率的表达式：

对于对数几率有

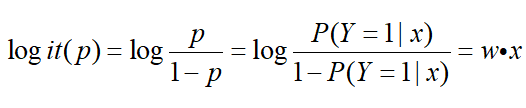
所以说，逻辑斯蒂回归模型是对数线性模型。

·学习策略（4.12.23.40）

模型参数估计采用极大似然法：
设

似然函数为：

对数似然函数为：

对ω求偏导数得到：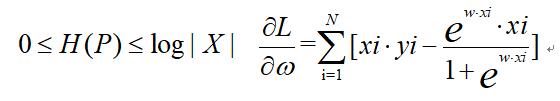

因此参数学习问题就变成了以对数似然函数为目标函数的最优化问题，常用方法为梯度下降法和牛顿法。

最大熵模型：

·适用范围

属于概率模型。最大熵原理认为要选择的概率模型首先要满足已有事实，即约束条件，而没有更多信息情况下，不确定部分是“等可能的”，由于“等可能”这个概念不方便优化操作，相反地熵可以作为优化的数值指标。
最大熵原理朴素解释为：凡是可考虑的因素之外的，均假设是均匀分布，也即等概率假设。它的原则是在所有满足约束条件的概率模型集合中选取熵最大的集合。
·熵的定义：

熵满足不等式

其中|X|为X取值的个数，当X分布式均匀分布时，H ( P ) 才取得最大值。

·最大熵模型的定义

最大熵应用到分类问题时，假设了这个模型是一个条件概率分布p(Y|X),即输入为x的条件下，输出为y的概率。
·输入输出
In:T={（x1，y1），（x2，y2），（x3，y3）……}
Out:P(Y|X)
·函数关系
根据训练数据集可以获得联合分布P(X,Y)与P(X)的经验分布

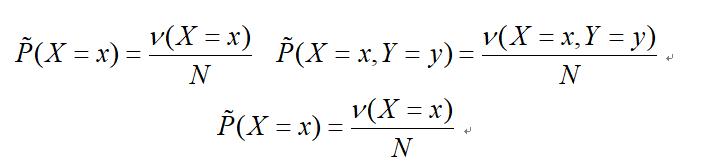
代表样本中x的频数。

·梯度下降法补充

在感知机时，我们应用了梯度下降作为优化算法，并第一次感受到数值迭代的方式解得最佳参数的快感。在逻辑斯蒂回归模型中，我们把优化目标划归成了求解使得似然函数最大值的参数，我们不妨将求解似然函数最大值问题当成优化目标，习惯上取其相反数作为损失函数，我们便可以继续应用梯度下降法进行优化了。
Tips:
为了应对过拟合，我们可以对损失函数进行正则化

，即损失函数中加入正则项。

其中，

即为正则项
注意：
1.引入正则项是为了应对过拟合，倾向于让模型参数更小。
2.模型参数小的时候，意味着模型更为“平滑”，这样输入改变的时候，输出的变化不会很剧烈，所以正则化后应该更加鲁棒。
3.参数问题：λ如果选的过大，那么损失函数会更倾向于考虑正则项，导致模型过于“平滑”，也会使得模型变得不准确，对train_data的准确率大大下降。

牛顿法

输入：特征函数f1,f2,f3,…,fn;经验分布P‘(x,y),目标函数f(ω)，模型

输出：最优参数值 ；最优模型

（1）对所有i∈{1，2，…,n}，取初值

（2）对每一i∈{1，2，…,n}，
(a) 令 是方程

的解，这里

（b）更新 ：

（3）如果不是所有 都收敛，重复步（2）

拟牛顿法

算法实现：

不失一般性也为了方便数据可视化，随机生成300个具有3个特征的数据。对数据进行某种函数关系映射，按照函数关系分为两类，一类label为1，一类为0；并将数据等分成两份一份用于训练，一份用于测试。随后用梯度下降法进行参数学习；运行结果如下：

close;
clear;
clc;
% 作者 M宝可梦
% 引用请注明出处 谢谢合作
%% 二分类:数据生成
data_num = 500;
Features=3;
data=rand(data_num,Features);
label=zeros(data_num,1);
data=[data,ones(data_num,1)];
% 数据预处理：通过设定某种关系进行预先二分类,打乱循序使得每次运行训练集和测试集和不同
for i = 1:data_num
    if 2*data(i,1)-data(i,2)+2*data(i,3)<1.5    % 代码可精简：label(2*data(:,1)-data(:,2)<0.5)=1; % 通过逻辑判断
        label(i)=1;
    end
end
randIndex = randperm(data_num);
data_new=data(randIndex,:);
label_new=label(randIndex,:);

%一半训练  一半测试
k=0.8*data_num;
train_data=data_new(1:k,:);
train_label=label_new(1:k,:);
test_data=data_new(k+1:end,:);
test_label=label_new(k+1:end,:);
[m1,n1] = size(train_data);
[m2,n2] = size(test_data);

%% 训练
%设定学习率delta;正则项系数;迭代次数;模型参数
delta=0.05; 
lambda=0.0001; 
num = 200;
theta=rand(1,Features+1);% 除w之外多一个偏置b
L=zeros(1,num);
for I = 1:num
    dt=zeros(1,Features);
    loss=0;
    for i=1:m1
        Data_Features=train_data(i,1:Features+1);
        Data_Label=train_label(i,1);
        
        h=1/(1+exp(-(theta * Data_Features'))); % h为P(Y=1|X) = exp(w·x)/[1+exp(w·x)]
        dt=(Data_Label-h) * Data_Features;   % 对数似然函数对w的求导
        theta=theta + delta*dt-lambda*theta; % 梯度下降法更新参数w
        loss=loss + Data_Label*log(h)+(1-Data_Label)*log(1-h);% 对数似然函数
    end
    % 由于问题划归为由极大似然估计估计参数，是对似然函数求极大值
    % 统一起见应用梯度下降法，归为对极大似然函数相反数的极小值求解，此处除以了样本数量，为平均损失
    loss=-loss/m1;
    L(I) = loss;% 作损失函数图
    
    if loss<0.001
        break;
    end
end

%% 作图
figure(1);
plot(L);
title('损失函数');
figure(2);
subplot(211);
plot3(data(label==1,1),data(label==1,2),data(label==1,3),'ro');
axis([0 1 0 1]);
title('正样本分类显示');
subplot(212);
plot3(data(label==0,1),data(label==0,2),data(label==0,3),'go');
axis([0 1 0 1]);
title('负样本分类显示');
figure(3);
plot3(data(label==1,1),data(label==1,2),data(label==1,3),'ro');
hold on;
plot3(data(label==0,1),data(label==0,2),data(label==0,3),'go');
axis([0 1 0 1]);
title('总体样本分类显示');
grid on

%% 测试准确率
acc=0;
for i=1:m2
    Data_Features=test_data(i,1:Features+1)';
    Data_Label=test_label(i);
    P_Y1=1/(1+exp(-theta * Data_Features));% P(Y=1|X) = exp(w·x)/[1+exp(w·x)]
    if P_Y1>0.5 && Data_Label==1
        acc=acc+1;
    elseif P_Y1<=0.5 && Data_Label==0
        acc=acc+1;
    end
end

fprintf('训练测试完成!\n应用模型：逻辑斯蒂回归\n优化算法：梯度下降\ntest_acc:%6.2f',acc/m2)

引用请注明出处 谢谢合作