基于图像相位相关性进行相邻图像检测

基于图像相位相关性进行相邻图像检测

学习笔记
《 Auto-sorting scheme for image ordering applications in image mosaicing》
作者:R. Song and J. Szymanski

算法思想及特点：

·两张图像相位相关性越高，输出的信号越逼近一个冲激信号，从峰值判断是否相邻
·其稳定性和可靠性不如基于特征的方法强健，但更快速
·该方法可以判断两幅图像是否重叠，以及重叠程度的大小

一 推导：

对于刚性的图像拼接任务，该方法假设两张图象I1,I2存在一定的平移x，平移部分也即图象的重合部分。

对两边取傅里叶变换有式子1-2

忽略傅里叶变换后频谱的幅值，取两边的相位关系有式1-3

再对1-3式取反变换，有式1-4

分析可知，如果我们假定两张图像混叠部分具有很高的相位相似性，两张图象的混叠程度越高，则 与 越接近，当比较理想状况下，有式1-5

而直流量的傅里叶反变换为冲击信号，不难理解混叠部分的相位相似性和冲激信号是呈现正相关的（相位相似度越高，反变换越逼近冲激信号，其表征图像相似度的信号峰值越高，以下称为SSP Similarity-Signal-Peak）。

二 多图像实现相邻性检测：

该方法实现的是依照两张图像的混叠部分进行相关性检测，因此对于多张图像的相邻关系判断需要采取一定的步骤，其解决的思路是两两进行配对计算SSP，根据SSP大小进行排序，越大说明图像的混叠部分相似性越高，也即相邻的可能性越高。优先拼接SSP值大的图像，拼错的可能性越小，一定程度上减小了累计误差。算法描述如下：

Maintaining

{ I1,I2,…IN } 待检测图像列表，初始共N张图像

<Ii,Ij>相邻图像对

1). 两两计算待检测图像的SSP，并据此排序，选择SSP最高的一对<Ii,Ij>作为本次相邻性判断的结论；
2). 采用一定的图像融合方法，将1)中结论中的两张图像<Ii,Ij>拼接成为图像Ik;
3). 将Ii,Ij从待检测图像列表删除，并将Ik加入待检测图像列表;
4. 如果待检测图像列表中只含一个图像，则算法完成，否则执行1)

2021.5.13
————————————————————————————
书接上回，本阶段完成相位相关性对位移的影响实验

三 关于具体位置的补充：

具体操作时，由于位移对应的是两张图像索引的概念，不仅要判断两张图像的是否相邻，更要解决两张图像上下左右的相互关系，即谁在谁左（右），谁在谁上（下），左平移多少，右平移多少。此处我采用了先实验再理论推导的方法，首先我选取了一张图像，在Y方向上进行截取并保证该方向上有一定重叠，（简单起见保持了尺度和旋转不变，相当于仅作平移操作）原图像如图3-1.

截取1-120列和100-219列作为测试图像，如图3-2，有明显的重叠部分

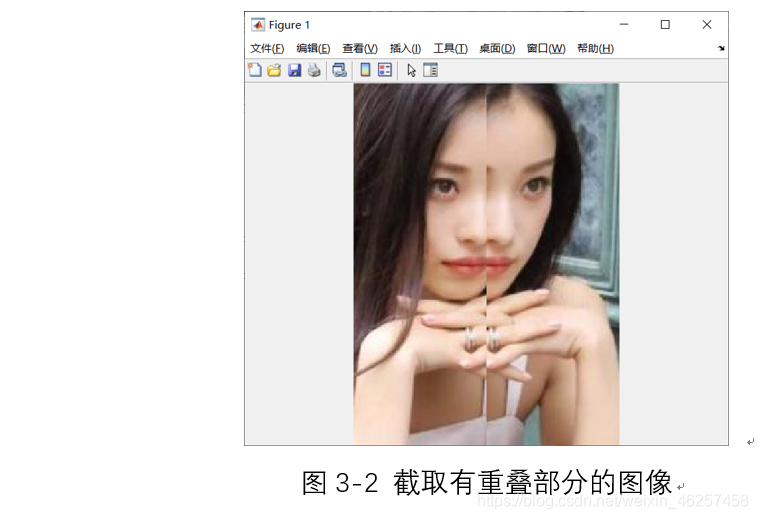
对两幅图像进行相位相关性计算。如方法中指出，如果选取一张图像进行自相位相关计算，得到的是一个单位冲击矩阵，冲激信号发生在索引为（1，1）处，也即不发生平移。如图3-3左下角.

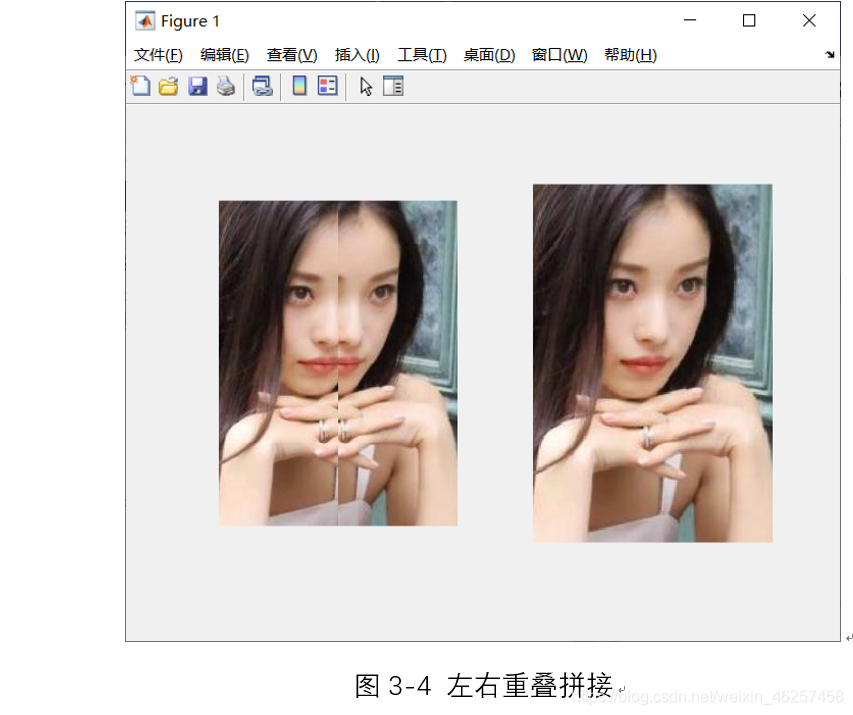
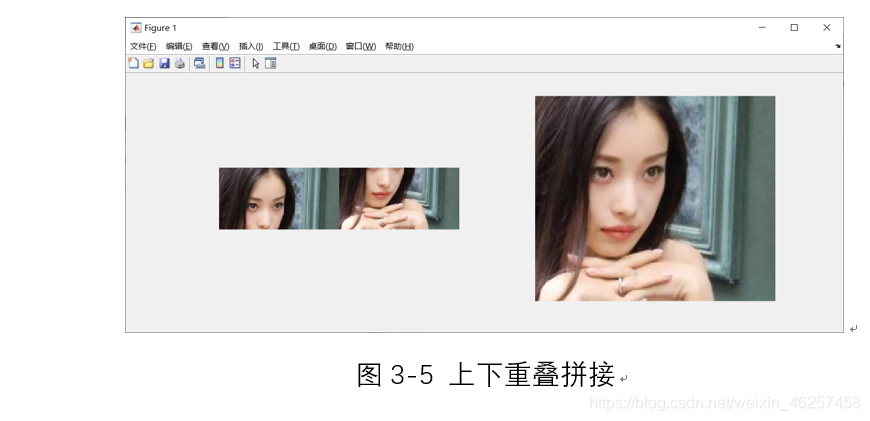
经过实验得到排布规律，并最终得到呈现效果如图3-4，3-5.


更为普遍地，需要解决的问题是上下左右均有平移的两张图像如何实现拼接任务。
更换数据集，将图3-6雏菊切分为F1,F2,F3…等若干图，并保证两两之间是有重叠部分，同时也保证了两张图片之间没有旋转以及尺度变换的关系。重新进行实验验证，选取了花朵较多的区域（便于我们观察位置关系）进行剪切如图3-7.


进行相位相关性检测实验结果如表3-1.

四 结论：

经过实验可知，文中方法可以有效的计算只存在位移关系的两张图的重叠度，并且可以有效的计算出两张图像准确的平移关系（包括两个方向）。
文中利用相位相似性进行相邻性检测，利用ssp大小判断两张图的重叠度大小，实现相邻性判断；并利用ssp得出拼接的顺序，重叠度越高的两张图优先拼接，相对于传统的特征提取的方式，更为快速。

五 思考与收获：

在阅读该文献时，对于推导部分中的位移关系进行了特别的关注，在实验中也发现，相位相似性检测可以找出两张图的位移关系（实验基于只存在位移关系，而不存在旋转以及尺度变换的两张图像）。
由其推导过程，我猜想能否用一种更为通用的表示，将旋转和尺度变换的关系也囊括进来，我做了部分理论推导（旋转关系），难点在于变换之后，坐标之间是耦合的。经过了解，傅里叶-梅林变换可以有效对抗图片中的位移-旋转-尺度变换。
2021.5.16
拼接剩余部分见下章
https://editor.youkuaiyun.com/md/?articleId=116944394

————————————————————————————