REINFORCEMENT LEARNING THROUGH ACTIVE INFERENCE

摘要

强化学习（RL）的核心原则是智能体寻求最大化累积奖励之和。相比之下，主动推理，认知和计算神经科学中的一个新兴框架，提出agent采取行动，以最大限度地提高有偏见的生成模型的证据。在这里，我们说明了来自主动推理的想法如何通过（i）提供探索和利用的内在平衡，以及（ii）提供更灵活的奖励概念来增强传统的RL方法。受主动推理的启发，我们开发并实现了一个新的决策目标，我们称之为预期未来的自由能。我们证明了所得到的算法成功地平衡了探索和利用，同时在几个具有挑战性的RL基准测试中实现了稳健的性能，具有稀疏，形状良好，没有奖励。

1.介绍

生物和人工智能都必须学会在未知的环境中做出适应性的决定。在强化学习（RL）领域，代理人的目标是学习一种策略，使期望回报的总和最大化（萨顿等人，（1998年）。该方法在诸如模拟游戏（Mnih等人，2015年;银等人，2017年）、机器人（Polydoros和Nalpanditis，2017年; Nagabandi等人，2019）和工业应用（Meyes等人，（2017年版）的领域中已经证明了令人印象深刻的结果。
相反，主动推理（Friston等人，二〇一六年;二〇一五年;二〇一二年; 2009年）–一个来自认知和计算神经科学的新兴框架–建议代理人选择行动，以便最大化偏向代理人偏好的模型的证明。该框架扩展了贝叶斯感知和学习的有影响力的理论（Knill & Pouget，2004; L Griffiths等人，2008）以结合概率决策，并且配备有生物学上合理的过程理论（Friston等人，2017年a），这一点得到了相当多的实证支持（Friston和Kiebel，2009年）。
虽然主动推理和RL有着不同的学科基础，但两种框架都在学习适应性行为问题上找到了相似的解决方案。例如，两个框架都强调了学习概率模型、进行推理和有效规划的重要性。这就引出了一个很自然的问题：主动推理的洞察力能为新的RL算法的发展提供信息吗？
从概念上讲，主动推理可以通过几种方式提供信息，并潜在地增强RL领域。首先，主动推理表明，代理人体现了他们其偏好环境的生成模型，并寻求最大化这一模型的证据。在这种情况下，奖励被认为是先验概率，而成功是根据首选结果和预期结果之间的差异来衡量的。将偏好制定为先验概率使在指定代理人目标时具有更大的灵活性(Friston等人，2012年；Friston，2019a)，为学习偏好提供了一种原则性(即贝叶斯)方法(Sajid等人，2019年)，并与最近的神经生理学数据相一致，表明了奖励表示的分布性质(Dabney等人，2020年)。其次，将奖励最大化重新表述为最大化模型证据，自然地涵盖单个目标下的探索和利用，从而无需向现有目标添加临时探索性术语。此外，正如我们将展示的那样，主动推理包含了一些已经建立的RL形式，表明了一个潜在的统一框架，用于不确定情况下的自适应决策。
事实证明，将这些概念性见解转化为RL的实际好处具有挑战性。目前主动推理的实现一般限于离散状态空间和玩具问题(Friston等人，2015；2017b；c)(尽管见(Tschantz等人，2019a；Millidge，2019；Catal等人，2019))。因此，还不可能评估主动推理在具有挑战性的环境中的有效性；因此，主动推理在RL社区中尚未被广泛采用。
在本文中，我们在决策的背景下考虑主动推理。我们提出并实现了一个新的主动推理目标函数–预期未来的自由能–并表明这个量为已经建立的RL目标提供了一个容易处理的界限。我们在一组具有挑战性的连续控制任务上对该算法的性能进行了评估。我们在稀疏、形状良好和没有奖励的环境中表现出了很强的性能，证明了我们的算法能够有效地平衡探索和利用。总之，我们的结果表明，主动推理是对现有RL方法的一种有前途的补充。

2.主动推理

主动推理和RL都可以在部分观察到的马尔可夫决策过程POMDP(Murphy，1982)的背景下提出。在每个时间步长t，环境st的真实状态根据随机转移动力学st∼p(st|st−1，at−1)而演变，其中
表示代理的动作。代理不一定能够访问环境的真实状态，而是可以根据ot∈p(ot|st)生成的接受状态(\mathrm{o}_t \in \mathbb{R}^{d_o}) 。在这种情况下，代理必须根据环境的真实状态st来执行操作。最后，环境根据rt∼p(rt|st)2生成奖励rt。

RL的目标是学习一种最大化预期奖励总和 E[∞t=0γtrt]的策略(Sutton等人，1998年)。相比之下，主动推理的目标是最大化代理的生成模型 pΦ(o，S，θ)的贝叶斯模型证据，其中θ∈Θ表示模型参数。
至关重要的是，主动推理允许代理人的生成模型偏向有利的事件状态(Friston，2019b)。换句话说，该模型将概率分配给观察空间中既有可能又有利于代理成功的部分。我们使用符号pΦ(·)表示编码代理偏好的任意分布。
给定一个生成模型，代理可以通过对任意分布Q(S，θ)进行编码并最小化变分自由能
来执行近似贝叶斯推理。当观测值 o 已知时，F可以通过标准变分方法最小化(Bishop，2006；Buckley et al.，2017)，导致q(S，θ)趋向真正的后验p(S，θ|o)。注意，将模型参数θ视为随机变量将学习投射为推理过程(Blundell等人，2015年)。
在当前上下文中，代理还维护对策略π={a0，…，at}的信念，这些策略本身就是随机变量。然后，通过识别最小化F的q(π)来实现策略选择，从而将策略选择塑造为一个近似推理的过程(Friston等人，2015年)。虽然标准自由能泛函F通常是针对单个时间点t定义的，但π指的是变量的时间序列。因此，我们增加自由能泛函F以包含未来变量，从而得到预期的未来F˜的自由能。这个量衡量了一系列关于未来变量的信念与代理人的有偏见的生成模型之间的 KL 散度。

现在的目标是推断q(π)以最小化F˜。我们证明，最终的方案自然包括探索和开发，因此暗示了推理、学习和决策之间的深层关系。

3.未来的自由能

设xt：T表示随时间变化的变量序列，xt：T = {xt，…，xT}的值。我们希望最小化预期未来F的自由能，其定义为：

其中q（ot：T，st：T，θ，π）表示智能体对未来变量的beliefs，pΦ（ot：T，st：T，θ）表示智能体的有偏生成模型。注意，关于未来变量的信念包括关于未来观测的信念，ot：T，它是未知的，因此被视为随机变量3。
为了找到使F最小的q（π），我们注意到（见附录C）：
附录C：最优策略的推导
我们推导出 q(π) 的分布，该分布使 F~ 最小化：


因此，当q（π）= σ（- F~π）时，预期未来的自由能最小化，或者换句话说，当政策最小化F ~ π时，政策更有可能。

3.1 EXPLORATION & EXPLOITATION.

为了直观地了解最小化 F~ π 所需要的内容，我们将代理的生成模型分解为，这意味着模型只在其信念上对观察有偏差。为了保持与RL术语的一致性，我们将“奖励”r视为单独的观察模态，使得pΦ（ot：T）指定首选奖励的分布。我们在附录E中描述了pΦ（ot：T）的实现。以类似的方式，
指定给定策略时对未来奖励的信念。
附录E：模型细节
在目前的工作中，我们使用基于集成的方法实现了概率模型（Chua 等人，2018a；Fort 等人，2019；Chitta 等人，2018）。 这里，维护在不同批次的数据集 D 上训练的点估计参数 θ = {θ0, …, θB} 的集合，并将其视为来自后验分布 p(θ|D) 的样本。 除了与主动推理框架保持一致之外，概率模型还能够主动解决模型不确定性，捕获认知不确定性和任意不确定性，并有助于避免低数据状态下的过度拟合（Fort et al., 2019；Chitta et al., 2018； Chatzilygeroudis 等人，2018；Chua 等人，2018b)。
这种设计选择意味着我们在评估对未来变量的信念时使用轨迹采样方法（Chua et al., 2018a），因为每次通过转换模型 p(st|st−1, θ, π) 都会从 st 中唤起 B 个样本 。
转移模型 我们将转移模型实现为 p(st|st−1, θ, π) 作为 N(st; fθ(st−1), fθ(st−1))，其中 fθ(·) 是一组函数 近似器 fθ(·) = {fθ0 (·), …, fθB (·)}。 在本文中，fθi (st−1) 是一个具有 400 个隐藏单元和 swish 激活函数的两层前馈网络。 根据之前的工作，我们预测状态增量而不是下一个状态（Shyam 等人，2018）。
奖励模型 我们将奖励模型实现为 p(oτ|sτ, θ, π) = N(oτ; fλ(sτ), 1)，其中 fλ(sτ) 是某个任意函数逼近器6。 在本文中，fλ(sτ) 是一个具有 400 个隐藏单元和 ReLU 激活函数的两层前馈网络。 学习奖励模型在主动推理框架之外提供了一些看似合理的好处，因为它废除了可以根据观察或状态直接计算奖励的要求（Chua 等人，2018a）。
全局先验 我们将全局先验 pΦ(o) 实现为高斯分布，其单位方差以相应环境的最大奖励为中心。 我们将其留给未来的工作来探索更复杂的先验的影响。

考虑到这种因式分解，很容易证明 - Fπ 分解为预期信息增益项和外在项（参见附录 B）4：

最大化等式4有两个功能性结果。
首先，它最大化预期的信息增益，这量化了智能体期望从执行某些策略中获得的信息量。由于智能体保持对环境状态和模型参数的信念，这个术语促进了状态和参数空间的探索。
第二，它最小化了外在项——即代理人对未来观察的（政策条件的）信念与其首选观察之间的 KL 散度。在当前情况下，它衡量智能体期望从策略中获得的奖励与智能体期望的奖励之间的 KL 差异。 总之，选择最小化 F~ 的策略会在勘探和开发之间实现自然平衡。

3.2 RELATIONSHIP TO PROBABILISTIC RL与概率强化学习的关系

近年来，有几种尝试在概率推理方面形式化RL(Levine，2018)，例如KL-Control(Rawlik，2013)、控制即推理(Kappen等人，2012年)和状态-边缘匹配(Lee等人，2019年)。在许多这些方法中，RL目标被广泛地概念化为最小化。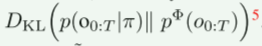
在附录D中，我们证明了预期的未来F˜的自由能为该目标提供了一个易于处理的界限：

这些结果表明，主动推理和现有的概率RL方法之间有很深的同源性。

4.IMPLEMENTATION

在这一部分中，我们描述了所提出的目标函数在基于模型的RL的上下文中的有效实现。为了选择动作，我们在每个时间步优化Q(π)，并执行最可能的策略指定的第一个动作。这需要(i)评估对未来变量Q(st：t，ot：t，θ|π)的信心的方法，(ii)评估Fπ的有效方法，以及(Iii)优化q(π)的方法，使得q(π)=σ(−Fπ)
评估对未来的信念，我们将对未来的信念分解并评估为：

这里我们将生成模型分解为p（oτ，sτ，θ| π）= p（oτ| sτ，π）p（sτ| sτ−1，θ，π）p（θ）.我们在附件E中描述了实现和学习的可能性p（oτ|sτ，π），跃迁模型p（sτ| sτ−1，θ，π）和参数先验p（θ）。
评估 F∼ π ，注意，其中H是规划范围。给定关于未来变量的信念，单个时间点的预期未来的自由能可以有效地计算为（参见附录G）：

在当前的论文中，代理观察环境st的真实状态，使得唯一的部分可观察性是在奖励rt中。因此，方程7的第二项是多余的，因为状态没有不确定性。第一（外在）项可以解析计算（见附录E）。我们在附录G中描述了我们对最后一项（参数信息增益）的近似。
优化策略分布我们选择将q（π）参数化为对角高斯分布。我们使用CEM算法（Rubinstein，1997）来优化q（π）的参数，使得q(π) ∝ −Fπ。虽然这种解决方案无法捕捉到−Fπ的确切形状，智能体只需要确定情况的顶峰即可制定最优策略。
在算法1中提供了用于推断q（π）的完整算法。

5.EXPERIMENTS

为了确定我们的算法是否成功地平衡了探索和利用，我们研究了其在以下领域的性能：（i）良好的奖励，（ii）极其稀疏的奖励和（iii）完全没有奖励。 我们总共使用四个任务。 对于稀疏奖励，我们使用 Mountain Car 和 Cup Catch 环境，其中代理仅在实现目标时获得奖励。 为了良好的奖励，我们使用具有挑战性的 Half Cheetah 环境，同时使用跑步和翻转任务。 对于没有奖励的领域，我们使用 Ant Maze 环境，其中没有奖励，成功通过迷宫覆盖的百分比来衡量（有关所有环境的详细信息，请参阅附录 H）。
对于稀疏回报的环境，我们将我们的算法与两条基线进行比较，(I)只基于外部项选择策略的奖励算法(即忽略参数信息增益)，以及(Ii)通过最大化转变模型的输出方差来寻找不确定转变的方差算法(见附录E)。请注意，方差代理还增加了外部项，以进行比较。
对于具有良好形状奖励的环境，我们将我们的算法与100集后由最先进的无模型RL算法获得的最大奖励进行了比较，软演员评论家(SAC)Haarnoja等人。(2018)，它通过寻求政策分布的最大熵来鼓励探索。
最后，对于没有奖励的环境，我们将我们的算法与随机基线进行比较，后者随机执行操作。
山车实验如图1a所示，我们将每集获得的总奖励绘制在25集上，其中每集最多有200个时间步长。这些结果表明，我们的算法快速探索并一致地达到目标，在一次试验中获得了最优性能。相比之下，基准算法平均无法成功探索并获得良好的性能。我们通过绘制有探索和没有探索的状态空间覆盖率来定性地证实这一结果(图2B)。我们的算法在CUP捕获环境中的性能与基准相当(图1B)。我们假设这是因为，虽然奖励结构在技术上是稀疏的，但它足够简单，可以通过随机动作达到目标，因此我们的方法提供的定向探索提供的好处很少

图1：（A）山地车：稀疏奖励山地车任务每集后的平均回报。我们的算法在单次试验中达到最佳性能。(B)Cup Catch：在稀疏奖励的Cup Catch任务中，每集之后的平均回报。在这里，算法之间的结果是相似的，所有代理在大约20集内达到渐近性能。（C & D）Half Cheetah：在形状良好的Half Cheetah环境中，分别针对跑步和翻转任务，每集之后的平均回报。我们将我们的结果与SAC在100集学习后的平均性能进行比较，证明我们的算法可以在不需要直接探索的环境中成功执行。每条线是5个种子的平均值，填充区域显示+/-标准差。
图1C和D表明，在挑战性的半猎豹任务上，我们的算法在100次发作后的性能明显优于最新的无模型算法。因此，我们的算法证明了在具有良好形状奖励的环境中的鲁棒性能，并且相对于SAC，在样本效率方面提供了相当大的改进。
最后用实例验证了此算法在没有奖励的环境中也能很好地执行，而只有探索的目标.图2B示出了我们的算法的探索速率实质上高于蚂蚁迷宫环境中的随机基线的速率，从而导致迷宫的更大部分被覆盖。这一结果表明，通过最小化预期未来的自由能所提供的定向探索在没有回报结构的环境中证明是有益的。
综上所述，这些结果表明，我们提出的算法–自然地平衡了探索和利用–可以成功地掌握具有各种奖励结构的挑战性领域。

图二：（A & B）Mountain Car状态空间覆盖：我们绘制了两个代理访问的状态空间中的点-一个最小化预期未来的自由能（FEEF），另一个最大化奖励。这些情节来自20集，显示FEEF代理几乎搜索了整个状态空间，而奖励代理仅限于通过随机动作到达的区域。©蚂蚁迷宫覆盖率：我们绘制了35次事件后迷宫覆盖率的曲线，比较了FEEF试剂与随机作用的试剂。这些结果是4粒种子的平均值。

6.DISCUSSION

尽管起源于不同的知识传统，但主动推理和强化学习都解决了未知环境中自适应决策的基本问题。利用这种概念上的重叠，我们已经应用了一个积极的推理角度的奖励最大化目标的强化学习，重铸为最小化期望和预期的未来之间的分歧。我们得出了一个新的目标，自然地平衡探索和利用，并在基于模型的RL上下文中实例化这个目标。我们的算法在各种已知对RL具有挑战性的环境中表现出强大的性能和灵活性。此外，我们已经表明，我们的算法适用于一组不同的奖励结构。相反，通过使用RL的工具实现主动推理，例如使用神经网络、深度集成和复杂的规划算法（CEM）进行摊销推理，我们已经证明了主动推理可以扩展到具有连续状态和动作空间的高维任务。
虽然我们的研究结果突出了主动推理和RL之间的现有重叠，我们最终重申两个方面的主动推理，可能是实用的RL。首先，将偏好表示为观察结果的分布允许在建模和学习非标量和非单调奖励函数时具有更大的灵活性。在复杂的非平稳环境中学习自然主义任务时，这可能是有益的。第二，内在价值和外在价值都是单一目标（预期未来的自由能量）的互补组成部分，这一事实可能为解决探索-开发困境提供了新的途径。我们的方法也承认有前途的方向，为今后的工作。这些包括研究不同分布对奖励的影响，将方法扩展到在时间和空间上分层的模型（Friston等人，2018; Pezzulo等人，2018年），并调查了与概率控制的替代公式的深层联系。

附录 A RELATED WORK

主动推理关于离散状态空间内的主动推理有大量文献，涵盖了各种各样的任务，例如眼跳中的认知觅食（Parr & Friston，2017；Friston，2019b；Schwartenbeck 等人，2019）、探索迷宫 （Friston 等人，2015；Pezzulo 等人，2016；Friston 等人，2016），玩 Atari 游戏（Cullen 等人，2018）。 主动推理还配备了完善的神经过程理论（Friston 等人，2017a；Parr 等人，2019），它可以解释大量的神经动力学。 之前也曾尝试将主动推理扩展到连续强化学习任务（Tschantz et al., 2019a; Millidge, 2019; Ueltzffer, 2018），我们在此基础上进行了构建。

基于模型的 RL 基于模型的强化学习最近得到了复兴，其实现大大超过了无模型方法的样本效率，同时也接近其渐近性能（Ha & Schmidhuber，2018；Nagabandi 等人，2018；Chua 等人） .，2018a；哈夫纳等人，2018）。 最近在 Atari（Kaiser 等人，2019）、高维机器人运动（Hafner 等人，2018；2019）和操纵（Nagabandi 等人，2019）任务等具有挑战性的领域取得了成功。 关键进展包括变分自动编码器（Kingma & Welling，2013）在部分观察的环境中灵活构建潜在空间、贝叶斯方法，例如反向传播贝叶斯（Houthooft 等人，2016a）、深度集成（Shyam 等人，2018；Chua 等人） ., 2018a) 和其他变分方法 (Okada & Taniguchi, 2019; Tschiatschek et al., 2018; Yarin Gal et al., 2016)，这些方法量化了动力学模型中的不确定性，并使模型能够学习一个潜在空间，即 对行动有用（Tschantz 等人，2019b；Watter 等人，2015）。 最后，强大的规划算法能够在连续状态和动作空间中进行在线规划，从而取得了进步（Williams 等人，2016 年；Rubinstein，1997 年）。

Intrinsic Measures 使用内在措施鼓励探索在强化学习中有着悠久的历史（Schmidhuber，1991；2007；Storck 等人，1995；Oudeyer 和 Kaplan，2009；Chentanez 等人，2005）。 最近文献中提出的无模型和基于模型的内在度量包括政策熵（Rawlik，2013；Rawlik等人，2013；Haarnoja等人，2018）、状态熵（Lee等人，2019） ）、信息增益（Houthooft et al., 2016b；Okada & Taniguchi, 2019；Kim et al., 2018；Shyam et al., 2019；Teigen, 2018）、预测误差（Pathak et al., 2017）、发散 集成（Shyam et al., 2019; Chua et al., 2018b）、不确定状态奖励（Bellemare et al., 2016; O’Donoghue et al., 2017）和赋权（de Abril & Kanai, 2018; Leibfried） 等人，2019；穆罕默德和雷森德，2015）。 信息增益在强化学习框架之外也有着悠久的历史，可以追溯到（Lindley，1956；Still & Precup，2012；Sun et al.，2011）。

附录 E MODEL DETAILS

在目前的工作中，我们使用基于集成的方法实现了概率模型（Chua 等人，2018a；Fort 等人，2019；Chitta 等人，2018）。 这里，维护在不同批次的数据集 D 上训练的点估计参数 θ = {θ0, …, θB} 的集合，并将其视为来自后验分布 p(θ|D) 的样本。 除了与主动推理框架保持一致之外，概率模型还能够主动解决模型不确定性，捕获认知不确定性和任意不确定性，并有助于避免低数据状态下的过度拟合（Fort et al., 2019；Chitta et al., 2018； Chatzilygeroudis 等人，2018；Chua 等人，2018b)。
这种设计选择意味着我们在评估对未来变量的信念时使用轨迹采样方法（Chua et al., 2018a），因为每次通过转换模型 p(st|st−1, θ, π) 都会从 st 中唤起 B 个样本 。
转移模型 我们将转移模型实现为 p(st|st−1, θ, π) 作为 N(st; fθ(st−1), fθ(st−1))，其中 fθ(·) 是一组函数 近似器 fθ(·) = {fθ0 (·), …, fθB (·)}。 在本文中，fθi (st−1) 是一个具有 400 个隐藏单元和 swish 激活函数的两层前馈网络。 根据之前的工作，我们预测状态增量而不是下一个状态（Shyam 等人，2018）。
奖励模型 我们将奖励模型实现为 p(oτ|sτ, θ, π) = N(oτ; fλ(sτ), 1)，其中 fλ(sτ) 是某个任意函数逼近器6。 在本文中，fλ(sτ) 是一个具有 400 个隐藏单元和 ReLU 激活函数的两层前馈网络。 学习奖励模型在主动推理框架之外提供了一些看似合理的好处，因为它废除了可以根据观察或状态直接计算奖励的要求（Chua 等人，2018a）。
全局先验 我们将全局先验 pΦ(o) 实现为高斯分布，其单位方差以相应环境的最大奖励为中心。 我们将其留给未来的工作来探索更复杂的先验的影响。

F IMPLEMENTATION DETAILS

对于所有任务，我们使用从随机代理收集的单集数据来初始化数据集 D。 对于每一集，我们使用负对数似然损失训练 100 个时期的集成转换模型和奖励模型。 我们发现每一集的冷启动训练都可以带来更一致的行为。 然后我们让智能体在基于算法1的环境中行动，并将收集到的数据附加到数据集D中。
下面列出了完整的超参数集：

G EXPECTED INFORMATION GAIN

在等式中。 如图 4 所示，预期参数信息增益以 的形式表示。 虽然这提供了关于信息增益项对行为的影响的良好直觉，但由于难以识别参数的真实后验，因此无法直接计算它。 我们在这里表明，通过贝叶斯规则的简单应用，可以直接导出预期信息增益的等效表达式，即状态似然与边际之间的差异，该表达式可分解为平均熵减去 平均熵：
第一项是熵的（负）平均值。 参数 θ 的平均值只需通过对系综中的动力学模型求平均值即可实现。 似然度 H[p(s|θ)] 的熵可以通过分析计算，因为集合中的每个网络都输出高斯分布，其中熵是已知的分析结果。 第二项是平均 H[Ep(θ)p(s|θ)] 的熵。 不幸的是，这个术语没有解析解。 然而，可以使用多种熵估计技术对其进行数值近似。 在我们的论文中，我们使用最近邻熵近似（Mirchev et al., 2018）。

H ENVIRONMENT DETAILS

山地汽车环境 (S ⊆ R2A ⊆ R1) 要求代理驾驶到山坡上，其中汽车驱动不足，需要它首先通过驾驶到对面的山上来获得动力。 当智能体达到目标时，奖励为 1，否则奖励为零。 接杯子环境 (S ⊆ R8A ⊆ R2) 要求智能体启动杯子并接住附着在其底部的球。 当智能体达到目标时，奖励为 1，否则奖励为零。 Half Cheetah 环境 (S ⊆ R17A ⊆ R6) 描述了正在运行的平面两足动物。 对于运行任务，收到的奖励为 v − 0.1||a||2，其中 v 是智能体的速度；对于翻转任务，收到的奖励为  − 0.1||a||2，其中  是角速度。 蚂蚁迷宫环境 (S ⊆ R29A ⊆ R8) 涉及一个四足代理探索矩形迷宫。