一、机器人路径规划介绍
移动机器人路径规划是机器人研究的重要分支,是对其进行控制的基础。根据环境信息的已知程度不同,路径规划分为基于环境信息已知的全局路径规划和基于环境信息未知或局部已知的局部路径规划。随着科技的快速发展以及机器人的大量应用,人们对机器人的要求也越来越高,尤其表现在对机器人的智能化方面的要求,而机器人自主路径规划是实现机器人智能化的重要步骤,路径规划是指规划机器人从起点位置出发,无碰撞、安全到达指定目标位置的最优路径。目前,常用的移动机器人全局路径规划方法很多,如栅格法和人工势场法。对于栅格法,当空间增大时,所需存储空间剧增,决策速度下降;而人工势场法容易产生局部最优解问题和死锁现象。随着智能控制技术的发展,出现了如遗传算法、粒子群优化算法、麻雀搜索算法、灰狼优化算法、鲸鱼优化算法等。
参考文献:
[1]史恩秀,陈敏敏,李俊,等.基于蚁群算法的移动机器人 全局路径规划 方法研究[J].农业机械学报, 2014, 45(6):5.DOI:CNKI:SUN:NYJX.0.2014-06-009.
[2]朱庆保,张玉兰.基于栅格法的机器人路径规划蚁群算法[J].机器人, 2005, 27(2):5.DOI:10.3321/j.issn:1002-0446.2005.02.008.
[3]曹新亮,王智文,冯晶,等.基于改进蚁群算法的机器人全局路径规划研究[J].计算机工程与科学, 2020, 42(3):7.DOI:CNKI:SUN:JSJK.0.2020-03-027.
二、栅格地图环境搭建
首先建立移动机器人工作环境,设移动机器人的工作空间为二维空间(记为RS),工作环境中的障碍物即为机床。在机器人运动过程中,障碍物为静止且大小不发生变化。按栅格法划分RS,移动机器人在栅格间行走。无障碍物的栅格为可行栅格,有障碍物的栅格为不可行栅格。栅格集包含所有栅格。栅格标识有:直角坐标法和序号法。本文采用序号标识法。
在移动机器人工作空间下按从左到右,从上到下的顺序,依次标记为序号1,2,3,···,n,每一个序号代表一个栅格。为了避免移动机器人与障碍物发生碰撞,可以将障碍物膨胀,障碍物在占原有栅格的同时,再占多个栅格,按 个栅格算。这种划分方法简单实用,能够满足环境模型与真实情况相符。从而使移动机器人在路径规划时畅通无阻。令S={1,2,3,···,N}为栅格序号集。根据上述对应关系,可知g(0,0)的序号为1,g(1,0)序号为2,直至g(X,Y)的序号为n。规划起始位置、目标位置均为任意且都属于S(但不在同一栅格内)。
在实际工作环境中,移动机器人工作环境是复杂多变的,且为三维空间。为了便于研究,本文对环境进行简化建模。栅格法是一种常用的环境表示方法,因其简单方便(二维环境),环境建模的复杂性小,因而本文环境建模采用栅格法。在栅格地图中,工作环境被划分为很多栅格,其中包括有障碍物和无障碍的栅格,在仿真程序中用0表示此栅格无障碍物,机器人可以通过此栅格,用1表示栅格有障碍物,机器人无法通过,需选择其他栅格。栅格的尺寸大小可根据工作环境中的障碍物尺寸以及安全距离进行设置。为了实现程序仿真,需要对栅格进行标识,如下图所示,以20x20的栅格环境为例来说明。

如上图所示,白色栅格表示无障碍物的栅格,黑色栅格则表示有障碍物的栅格,在地图中对每个栅格编号,不同序号的栅格在坐标系中的坐标可用下式来表示:
x = mod ( N i / N ) − 0.5 x = \text{mod}(N_i / N) - 0.5 x=mod(Ni/N)−0.5
y = N − ceil ( N i / N ) + 0.5 y = N - \text{ceil}(N_i / N) + 0.5 y=N−ceil(Ni/N)+0.5
其中, mod \text{mod} mod为取余运算, ceil \text{ceil} ceil表示向后取整, N i N_i Ni是对应栅格的标号, N N N表示每列的栅格数量,取栅格中心位置作为栅格在坐标系中的坐标。这样机器人全局路径规划的问题就转变成了利用算法在栅格地图上寻找由起始点到目标点的有序的栅格子集,这些栅格子集的中心连线便是算法寻找的路径。
参考文献:
[1]史恩秀,陈敏敏,李俊,等.基于蚁群算法的移动机器人全局路径规划方法研究[J].农业机械学报, 2014, 45(6):5.DOI:CNKI:SUN:NYJX.0.2014-06-009.
[2]曹新亮,王智文,冯晶,等.基于改进蚁群算法的机器人全局路径规划研究[J].计算机工程与科学, 2020, 42(3):7.DOI:CNKI:SUN:JSJK.0.2020-03-027.
三、机器人路径规划多目标模型
3.1 路径成本
当机器人从起点向目标点移动时,通常选择最短的一条路径。将一条路径上每条线段的长度累加求和即可得到路径总长度。任何两点形成的线段都是根据欧氏距离来计算的,其中, P = [ P 0 , P 1 , … , P i , P i + 1 , … , P n , P n + 1 ] P = [P_0, P_1, \ldots, P_i, P_{i+1}, \ldots, P_n, P_{n+1}] P=[P0,P1,…,Pi,Pi+1,…,Pn,Pn+1]代表路径 P P P, S = P 0 S = P_0 S=P0代表起点, T = P n + 1 T = P_{n+1} T=Pn+1代表目标点。路径长度目标计算方法如下式:
Length ( P ) = ∑ i = 0 n d ( P i , P i + 1 ) \text{Length}(P) = \sum_{i=0}^{n} d(P_i, P_{i+1}) Length(P)=i=0∑nd(Pi,Pi+1)
其中, P i = ( x i , y i ) P_i = (x_i, y_i) Pi=(xi,yi) 和 P i + 1 = ( x i + 1 , y i + 1 ) P_{i+1} = (x_{i+1}, y_{i+1}) Pi+1=(xi+1,yi+1) 是路径中的两个连续点, d ( P i , P i + 1 ) d(P_i, P_{i+1}) d(Pi,Pi+1) 是路径中的线段距离; Length ( P ) \text{Length}(P) Length(P) 表示由所有线段相加得到的总路径长度; n n n 表示路径中的点数量。
3.2 平滑成本
路径平滑度表示路径的弯曲程度,换句话说,只有当路径是平滑的,机器人在移动时才会使用较少的能量。为了衡量可行路径的平滑度,使用两个连续路段之间的夹角 Ang [ P i , P i + 1 , P i + 2 ] \text{Ang}[P_i, P_{i+1}, P_{i+2}] Ang[Pi,Pi+1,Pi+2] 表示。路径平滑度的计算方法如下式:
Smoothness ( P ) = ∑ i = 0 n − 2 ∣ θ i ∣ \text{Smoothness}(P) = \sum_{i=0}^{n-2} \left| \theta_i \right| Smoothness(P)=i=0∑n−2∣θi∣
其中, θ i \theta_i θi 是路径上三个相邻点 P i , P i + 1 , P i + 2 P_i, P_{i+1}, P_{i+2} Pi,Pi+1,Pi+2 之间的夹角。
3.3 目标函数
移动机器人路径规划的目标函数 f 1 f_1 f1 和 f 2 f_2 f2 分别是路径成本最小和平滑成本最小:
f 1 = min ( Length ( P ) ) f_1 = \min(\text{Length}(P)) f1=min(Length(P))
f 2 = min ( Smoothness ( P ) ) f_2 = \min(\text{Smoothness}(P)) f2=min(Smoothness(P))
参考文献:
[1]于振翱. 面向多目标优化的移动机器人路径规划方法研究[D]. 山东:聊城大学,2023.
[2]杨嘉. 基于改进NSGA-Ⅱ算法的移动机器人路径规划研究[D]. 陕西:长安大学,2021.
四、NSWOA求解移动机器人路径规划
4.1基于非支配排序的鲸鱼优化算法
基于非支配排序的鲸鱼优化算法(Non-Dominated Sorting Whale Optimization Algorithm,NSWOA)是一种基于鲸鱼群体行为的多目标优化算法。它通过模拟座头鲸的捕猎行为,如收缩包围、螺旋运动和随机搜索等,结合非支配排序和精英保留策略来求解多目标优化问题,旨在找到一组 Pareto 最优解。
4.1.1 初始化种群
在解空间中随机生成一组鲸鱼个体,每个个体代表一个潜在的解。同时初始化算法的相关参数,如种群大小、迭代次数等。
4.1.2 适应度计算
根据目标函数计算每个个体的适应度,评估个体在多目标空间中的性能。
4.1.3 非支配排序
将种群中的个体按照非支配关系进行分层排序,划分出不同的等级。未被任何个体支配的个体属于第一层,然后从未被支配的个体中继续找出下一层,依次类推。等级越低的个体越优。
4.1.4 拥挤度计算
为了保持种群的多样性,在同一层的个体中,计算每个个体的拥挤度。拥挤度反映了个体周围解的密集程度,拥挤度越大,表示该个体周围的解越稀疏,有助于在选择操作中保留多样性的解。
4.1.5 精英保留策略
保留当前种群中的精英个体,即非支配排序中等级较高的个体,确保这些优质解能够进入下一代种群,避免优秀解的丢失,同时为后续的迭代提供更好的起点。
4.1.6 位置更新
根据鲸鱼优化算法的捕猎行为,更新鲸鱼的位置:
- 收缩包围:以当前最优解为中心,逐步缩小搜索范围,使个体向最优解靠近。
- 螺旋运动:模拟鲸鱼围绕猎物的螺旋式运动,增加搜索的多样性。
- 随机搜索:随机选择一个个体作为目标,进行位置更新,以探索新的解空间。
4.1.7 适应度评估与选择
计算新位置个体的适应度,并根据非支配排序和拥挤度计算,选择下一代种群中的个体。通过比较当前个体和新生成个体的优劣,保留更优的解,推动种群向更优区域进化。
4.1.8 终止条件判断
判断是否达到预设的迭代次数或其他终止条件。如果满足条件,则停止迭代,输出 Pareto 最优解集;否则,继续进行迭代。
参考文献:
[1]JANGIR P,JANGIR N. Non-dominated sorting whale optimization algorithm (NSWOA): a multi-objective optimization algorithm for solving engineering design problems[J]. Global journals of research in engineering, 2017;17: 15-42.
4.2 部分代码
close all
clear
clc
dbstop if all error
addpath("./ /")
global G S E
MultiObj= fun_info();%获取无人机模型信息
params.maxgen=100; % 最大迭代次数
params.Np=50; % 种群大小
params.Nr=100; %外部存档大小(不得小于种群大小)
[Xbest,Fbest] = (params,MultiObj);
%% 获取算法得到的所有路径存于Result中
for i=1:size(Xbest,1)
global_best = round(Xbest(i,:));
route = [S(1) global_best E(1)];
path=generateContinuousRoute(route,G);
% path=shortenRoute(path);
path=GenerateSmoothPath(path,G);
Result(i).BestPosition= path;
Result(i).BestFit=Fbest(i,:);
end
%% 获取 路径成本最小 与 平滑成本最小
if size(Fbest,1)>1
idx=min(Fbest);
else
idx=Fbest;
end
KK=find(Fbest(:,1)==idx(1));
IDX(1)=KK(1);
KK=find(Fbest(:,2)==idx(2));
IDX(2)=KK(1);
%% 画图pareto前沿图
dbclear all
figure
plot(Fbest(:,1),Fbest(:,2),'r*');
xlabel('路径成本')
ylabel('平滑成本')
legend('')
4.3 部分结果

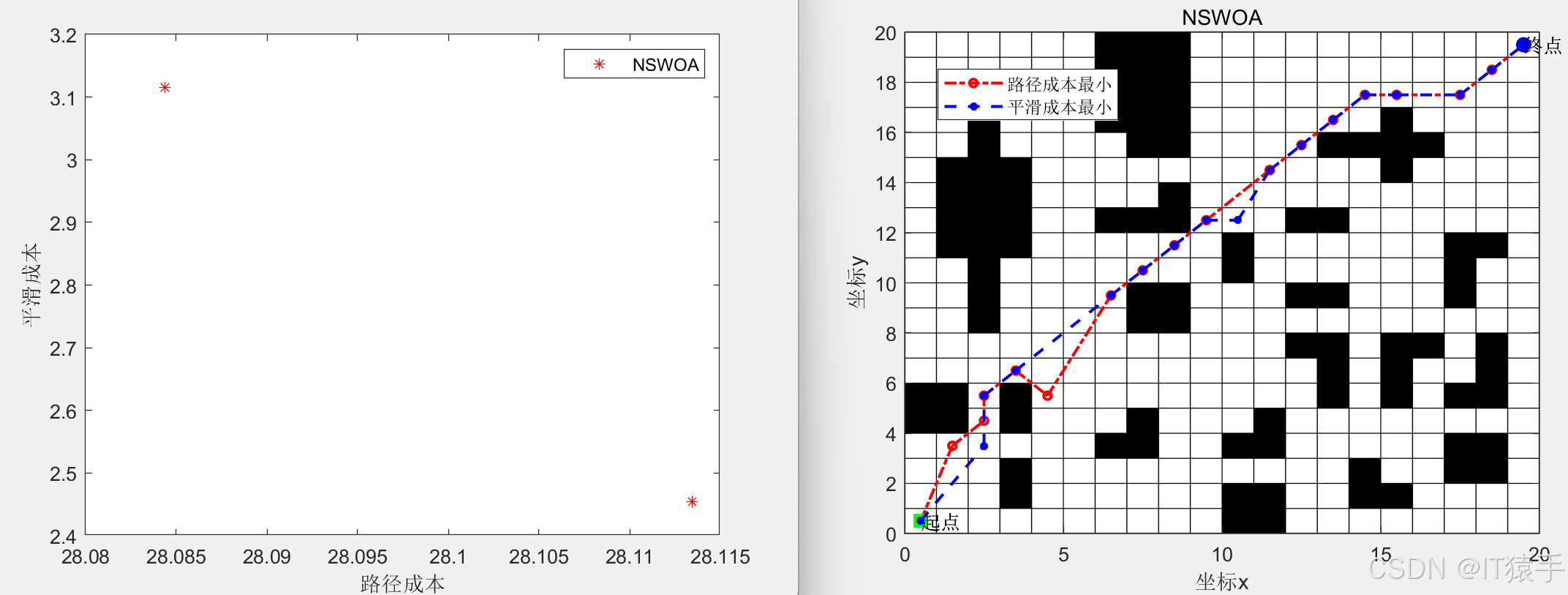
五、完整MATLAB代码
见下方联系方式




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








