归并排序算法求逆序数

归并算法分析

归并排序是一种稳定的排序且效率是比较高的，核心是分治法。
归并排序即是把一个无序数列不断拆分成n个子序列，直到子序列剩余两个时，将这n个子序列排序，然后合并起来，变成一个有序数列。时间复杂度为O(nlogn)。

序列
1 9 8 7 5 4
归并排序的步骤如图所示

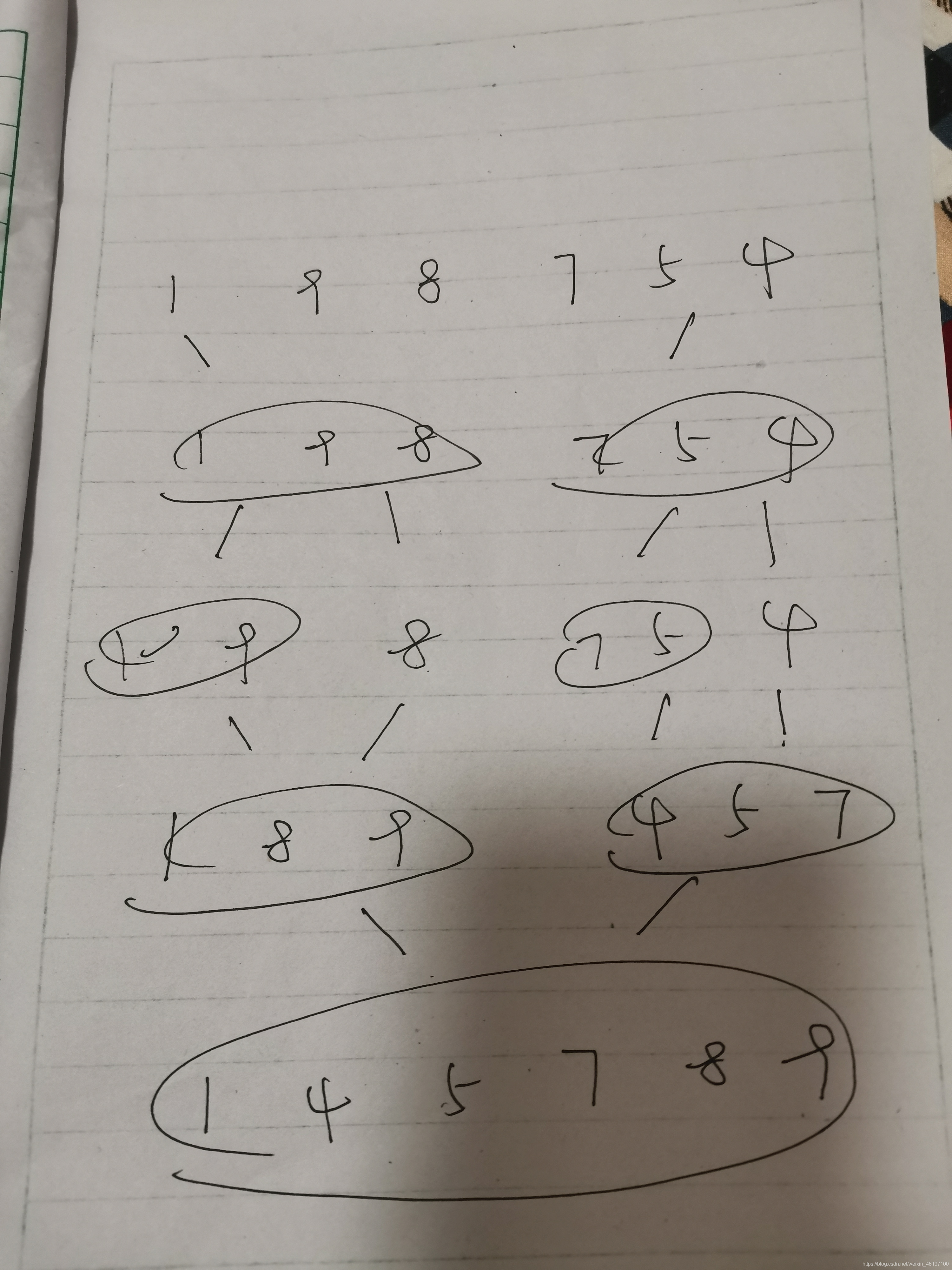
例如

描述
在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。

现在，给你一个N个元素的序列，请你判断出它的逆序数是多少。

比如 1 3 2 的逆序数就是1。

格式
输入格式
第一行输入一个整数T表示测试数据的组数（1<=T<=5)
每组测试数据的每一行是一个整数N表示数列中共有N个元素（2〈=N〈=100000）
随后的一行共有N个整数Ai(0<=Ai<1000000000)，表示数列中的所有元素。

数据保证在多组测试数据中，多于10万个数的测试数据最多只有一组。

输出格式
输出该数列的逆序数

#include<stdio.h>
#include<stdlib.h>
long long count;
void fun(long long a[],long long l,long long mid,long long r)
{
   
    long long low,mid1,mid2,high,i,j,k=0;