Chan算法原理
TDOA(TDOA，the time differences of arrival，到达时间差)，Chan算法是TDOA定位方法的一个很好用的方法。
Chan算法是非递归双曲线方程组解法，具有解析表达式解，主要特点是：在测量误差服从理想高斯分布时，它的定位精度高、计算量小，并且可以通过增加已确定点的数量来提高算法精度。
该算法的推导前提是基于测量误差为零均值高斯随机变量，对于实际环境中误差较大的测量值，比如在有非视距误差的环境下，该算法的性能会有显著下降。二维情况下，可分为只有三个点参与定位和三个点以上参与定位。
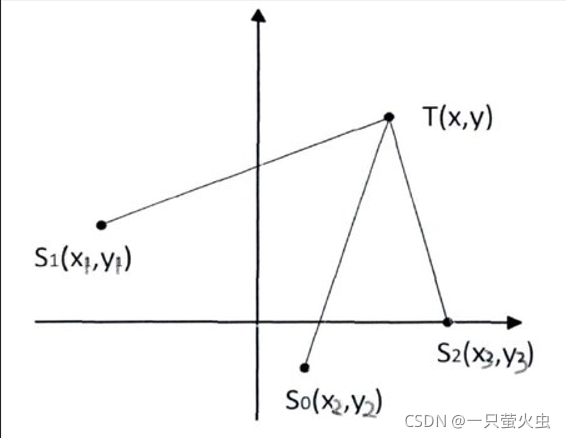
已知坐标(x1,y1),(x2,y2),(x3,y3)(x_1, y_1), (x_2, y_2), (x_3, y_3)(x1,y1),(x2,y2),(x3,y3)，假设第未知点的坐标是(x,y)(x, y)(x,y)根据几何关系定义一下关系表达式：
ri=(xi−x)2+(yi−y)2r_i = \sqrt{(x_i-x)^2+(y_i-y)^2}ri=(xi−x)2+(yi−y)2 ………(1)\dots\dots\dots(1)………(1)
ri,1=ri−r1=(xi−x)2+(yi−y)2−(x1−x)2+(y1−y)2r_{i,1}=r_i-r_1=\sqrt{(x_i-x)^2+(y_i-y)^2}-\sqrt{(x_1-x)^2+(y_1-y)^2}ri,1=ri−r1=(xi−x)2+(yi−y)2−(x1−x)2+(y1−y)2
最低0.47元/天 解锁文章
扫一扫
762
到【灌水乐园】发言
