体积
平行截面面积已知的立体的体积：
空间立体介于垂直于x 轴的两个平面x=a与x=b（a<b）之间，用垂直于x轴的平面去截立体，若所得截面面积是关于x的已知连续函数S(x)，立体的体积为 :
V
=
∫
a
b
f
(
x
)
d
x
V=\int_a^b f(x) \mathrm d x
V=∫abf(x)dx．
旋转体体积
1.：由连续曲线 y=f(x)(f(x)
≥
0
\ge0
≥0)和直线 x=a，x=b(a<b) 及 y=0所围
成的平面图形绕x轴旋转一周所成旋转体的体积为:
V
=
π
∫
a
b
f
2
(
x
)
d
x
V=\pi \int_a^b f^2(x) \mathrm dx
V=π∫abf2(x)dx
2.由连续曲线y=f(x)(
f
(
x
)
≤
0
f(x)\le0
f(x)≤0)和直线
x
=
a
x=a
x=a，
x
=
b
x=b
x=b及
y
=
0
y=0
y=0所围成的平面图
形绕 y 轴旋转一周所成旋转体的体积为:
V
=
2
π
∫
a
b
x
f
(
x
)
d
x
V=2\pi\int_a^bxf(x) \mathrm dx
V=2π∫abxf(x)dx
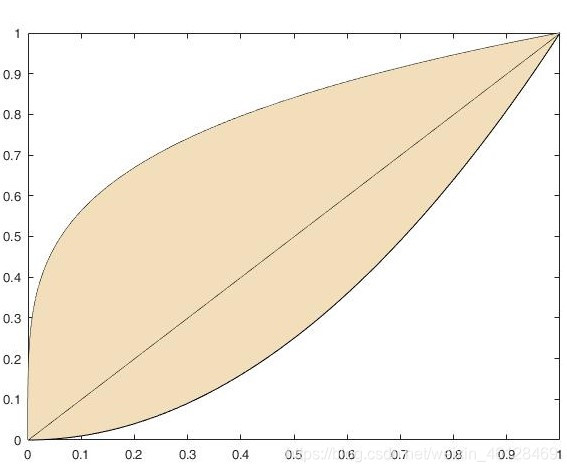
例：求由曲线 y = x 2 , x = y 2 y=x^2,x=y^2 y=x2,x=y2所围图形分别绕x轴与 y 轴旋转产生的立体的体积.
绕x轴：
V
=
π
∫
0
1
x
−
x
4
d
x
=
3
10
π
V=\pi\int_0^1 x-x^4 \mathrm dx=\frac3{10}\pi
V=π∫01x−x4dx=103π
绕y轴：
V
=
2
π
∫
0
1
x
(
x
−
x
2
)
d
x
=
3
10
π
V=2\pi\int_0^1 x(\sqrt{x}-x^2) \mathrm dx=\frac3{10}\pi
V=2π∫01x(x−x2)dx=103π
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
