汉诺塔问题

视频讲解：汉诺塔问题-10分钟解决

一、题目

【题目描述】

约19世纪末，在欧州的商店中出售一种智力玩具，在一块铜板上有三根杆，最左边的杆上自上而下、由小到大顺序串着由64个圆盘构成的塔。目的是将最左边杆上的盘全部移到中间的杆上，条件是一次只能移动一个盘，且不允许大盘放在小盘的上面。

这是一个著名的问题，几乎所有的教材上都有这个问题。由于条件是一次只能移动一个盘，且不允许大盘放在小盘上面，所以64个盘的移动次数是：18,446,744,073,709,551,615

这是一个天文数字，若每一微秒可能计算(并不输出)一次移动，那么也需要几乎一百万年。我们仅能找出问题的解决方法并解决较小N值时的汉诺塔，但很难用计算机解决64层的汉诺塔。

假定圆盘从小到大编号为1, 2, ...

【输入】

输入为一个整数(小于20）后面跟三个单字符字符串。

整数为盘子的数目，后三个字符表示三个杆子的编号。

【输出】

输出每一步移动盘子的记录。一次移动一行。

每次移动的记录为例如 a->3->b 的形式，即把编号为3的盘子从a杆移至b杆。

【输入样例】

2 a b c

【输出样例】

a->1->c
a->2->b
c->1->b

二、做题思路

1.移动的基本策略

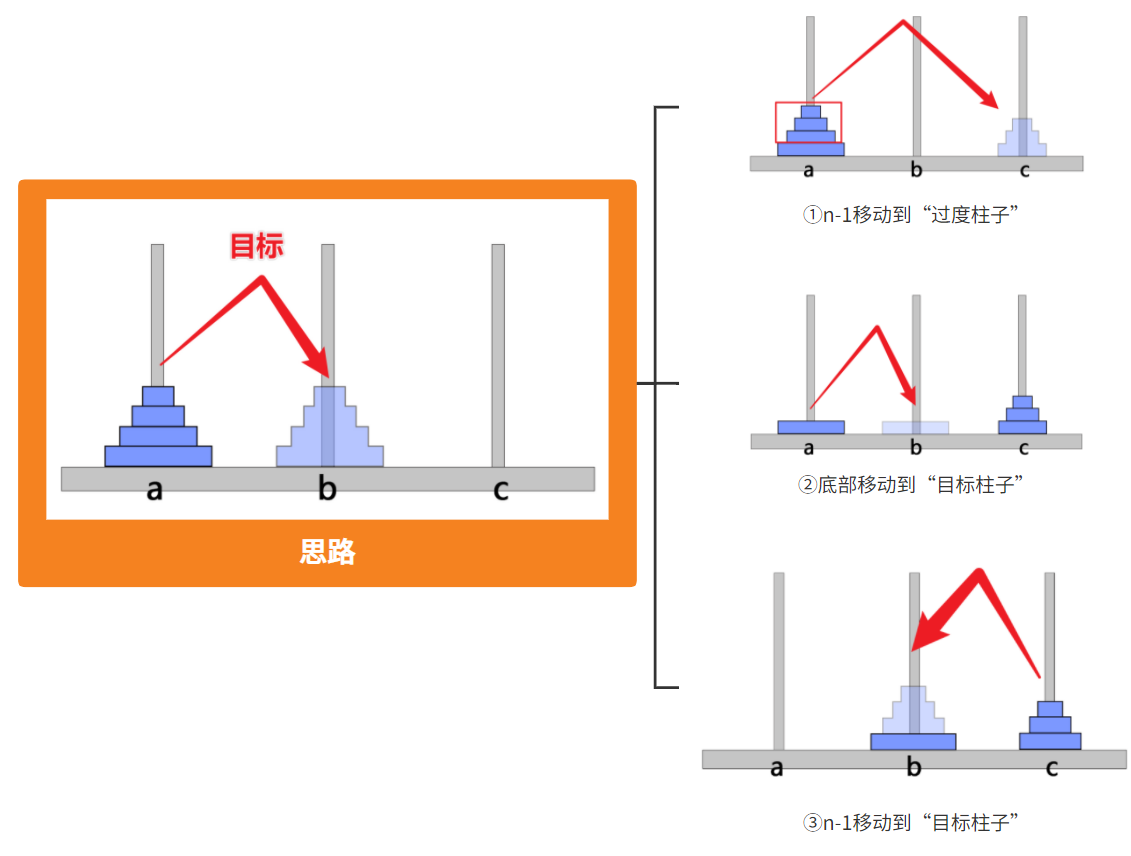
2.拆解步骤①

按照原来的方法，达到原来的目标，再将b、c柱子做交换，即可发现，其实方法和原来一样

3.拆解步骤③

与拆解步骤①相同

4.以此类推

三、代码实现

#include<iostream>
using namespace std;
void hanoi(int now,char source,char target,char auxiliary){
	if(now==0) return;
	//①n-1移动到“过度柱子”
	hanoi(now-1,source,auxiliary,target);
	//②底部移动到“目标柱子”
	printf("%c->%d->%c\n",source,now,target);
	//③n-1移动到“目标柱子”
	hanoi(now-1,auxiliary,target,source);
}
int main(){
	//1)输入数量n，柱子的编号
	int n;
	char a,b,c;
	cin>>n>>a>>b>>c;
	//2)递归实现"汉诺塔"
	hanoi(n,a,b,c); 
}