常见的排序算法——从青铜到王者，手把手教学

排序

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
排序稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次 序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排 序算法是稳定的；否则称为不稳定的。
常见排序算法

1、插入排序

1.1 直接插入排序

直接插入排序的基本思想：直接插入排序是一种简单的插入排序法，其基本思想是：把待排序的记录按其关键码值的大小逐个插入到一 个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列 。
实现方法：当我们插入第i个元素时，前i-1个元素都已经排好序了，此时只需要将第i个元素于前i-1个元素依次比较，然后在合适的位置插入元素即可。

代码

void InsertSort(int*a, int n)
{
   
	//实现多趟排序 
	for (int i = 0; i < n - 1; ++i)
	{
   

		//把tmp插入到数组的[0，end]有序区间中
		int end=i;
		int tmp=a[end+1];
		while (end >= 0)
		{
   
			//升序
			if (tmp < a[end])//如果出现了比a[end]大的数
			{
   
				a[end + 1] = a[end];//就将a[end]的数换到a[end + 1]位置上
				--end;//这样做的好处是，每次end+1这个位置是空的
			}
			else
			{
   
				break;
			}
		}
		a[end + 1] = tmp;
	}
}

直接插入排序总结：

1. 元素集合越接近有序，直接插入排序算法的时间效率越高
2. 时间复杂度（和冒泡排序一样）：O(N^2)（最坏情况：逆序。最好情况：O（N），顺序有序，和需要的顺序一致 ）
3. 空间复杂度：O(1)，它是一种稳定的排序算法
4. 稳定性：稳定

1.2希尔排序（缩小增量排序）

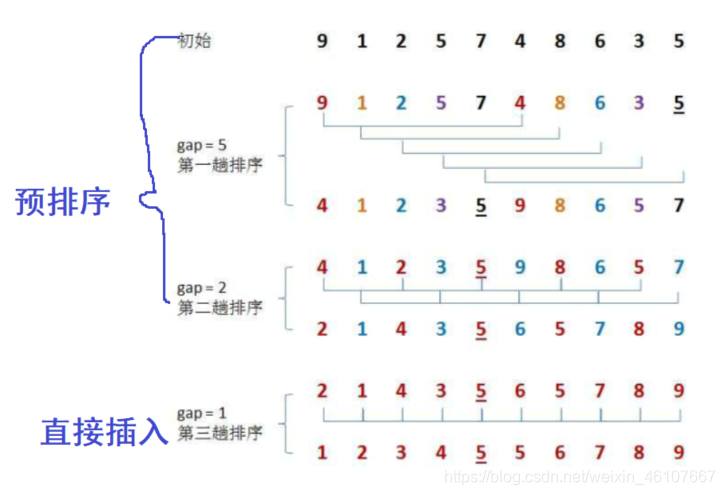
希尔排序的基本思想： 站在插入排序之上，分成预排序（让数组接近有序）、直接插入排序。先分组，对分组的数据插入排序。
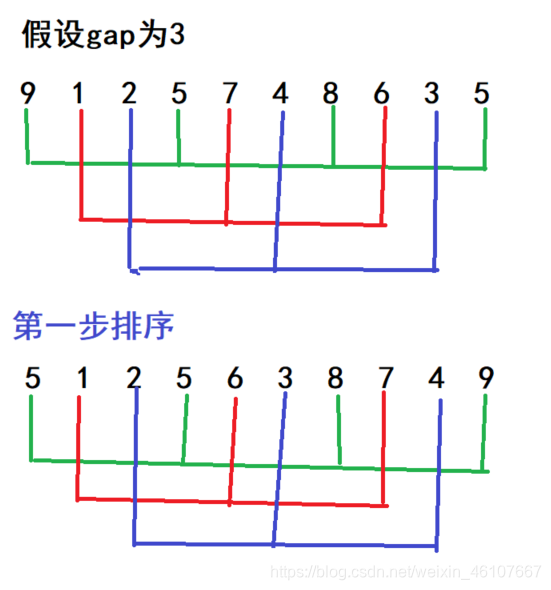
希尔排序实现方法：将整个数组间隔位gap分为一组，对组内进行插入排序。 每当进行一次排序，gap就要减小一点，到最后一次gap为1.
注意：当gap越大时，大的数和小的数可以更快的挪到对应的方向去。如果gap等于1，其实就是直接插入排序。


代码实现

//希尔排序
void ShellSort(int*a, int n)
{
   
	int gap = n;
	while (gap > 1)
	{
   
		gap = (gap / 3+1);//保证在最后gap为1
		//第一次预排序
		for (int i = 0; i < n - gap; ++i)
		{
   
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
   
				if (tmp < a[end])
				{
   
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
   
					break;
				}
			}
			a[end + gap] = tmp;
		}
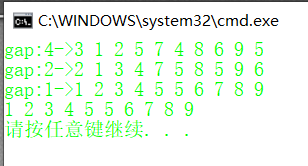
		printf("gap:%d->", gap);//显示每次gap是多少
		PrintArray(a, n);//数组打印函数
	}	
}

运行结果

2 选择排序

2.1 选择排序

选择排序基本思想：遍历一次选出最大值和最小值，然后放到数组的开头和末尾。

代码实现

//选择排序
void SelectSort(int* a, int n)
{
   
	int left = 0, right = n - 1;
	while (left < right)
	{
   
		int minIndex = left, maxIndex = left;
		//一次遍历就可以选出最大值和最小值
		for (int i = left; i <= right; ++i)
		{
   
			//选出最小的数
			if (a[i] < a[minIndex])
			{
   
				minIndex = i;
			}
			//选出最大的数
			if (a[i]>a[maxIndex])
			{
   
				maxIndex = i;
			}
		}
		//将最小的数放到数组开头
		Swap(&a[left], &a[minIndex]);
		if (left == maxIndex)
		{
   
			maxIndex = minIndex;
		}
		//将最大的数放到数组末尾
		Swap(&a[right], &a[maxIndex]);
		++left;
		--right;
	}
}

2.2堆排序

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是 通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。（如果排升序建立小堆，虽然可以选择出最小值，但是选择完后就会使接下来的堆的顺序变乱）
堆排序实现方法：将数组按照堆的顺序排列，先将堆按照向下调整算法变为大堆，然后将头尾数据交换，这样原有的堆的父子关系不会发生变化，然后在按照向下调整算法将堆调整为大堆（就是将最大值放在第一位），然后再用倒数第二位数与第一位数进行交换。

代码实现

//堆排序
//向下调整
void AdjustDown(int* a, int n, int root)<