Mandelbrot Set with HPC【高性能计算导论课设】

---

title: Mandelbrot Set
date: 2022-01-13 15:39:18
tags: 高性能计算

Mandelbrot Set with HPC

本课程设计任务

使用MPI与OpenMP混合并行编程模型，计算一定范围复平面内属于Mandelbrot Set的元素。

将该范围复平面内的元素C是否属于Mandelbrot Set的信息，映射到图片中进行可视化。

调整并行进程数以及每个进程内的并行线程数，探究计算效率的变化情况。

调整数据规模，探究计算效率的变化情况。

计算策略

$$z_{n+1}=z_n^2+c$$

根据该公式，可以对某一个复平面的元素C进行迭代，从而得到z的数列，当该数列收敛，则该C属于Mandelbrot Set。
但是计算机无法处理无限迭代的问题，于是我们给出一个Limit，当迭代Limit次数列还没有发散时，就将对应的C近似列入Mandelbrot Set。

有文献证明，当|z| > 2时，z会迅速发散，所以这里我们近似地认为当出现模大于2的z时，该C下z的迭代数列发散。

将复平面内所有的C分为两类：

（1）迭代次数达到Limit还数列没有发散的。
（2）迭代次数达到n（<Limit）数列就已经发散的。

用矩阵记录下它们的类型，（1）记录为0，（2）记录为发散前最大迭代次数。

可视化策略

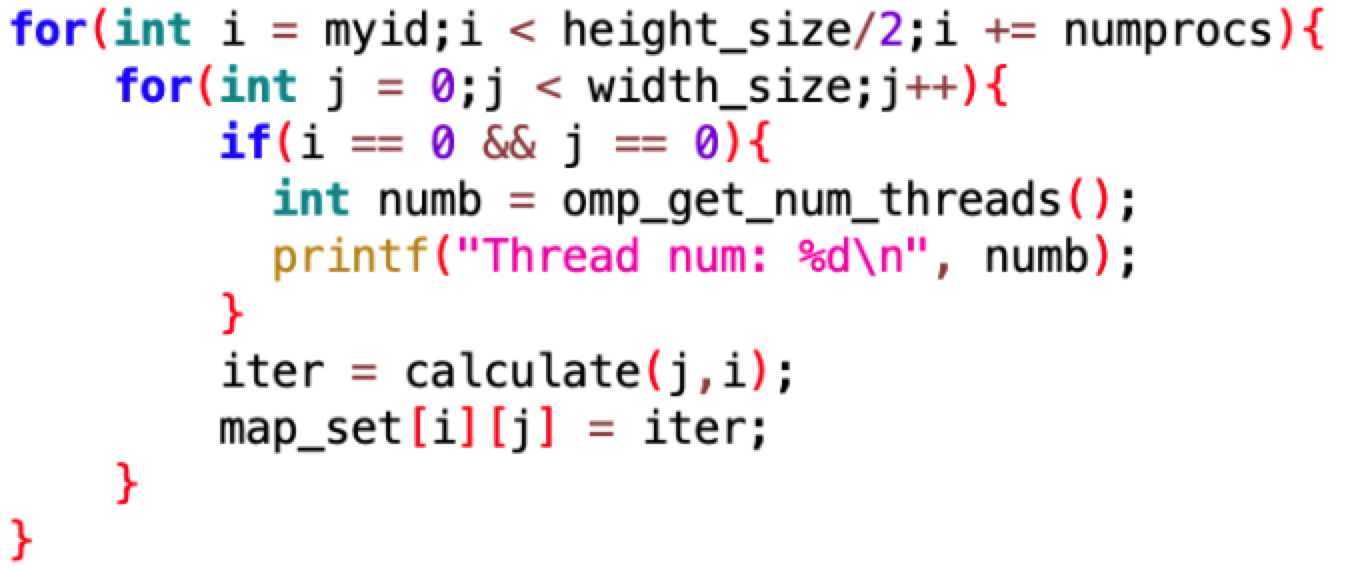
根据示例，我们的输出图片设置为长宽比4:3。

要将复平面的点映射到图片的坐标系中，映射的策略如下。

这里除的目的是将c的虚部限制在(-1,1)，实部限制在(-2,1)。

并行优化策略

优化策略（1）：

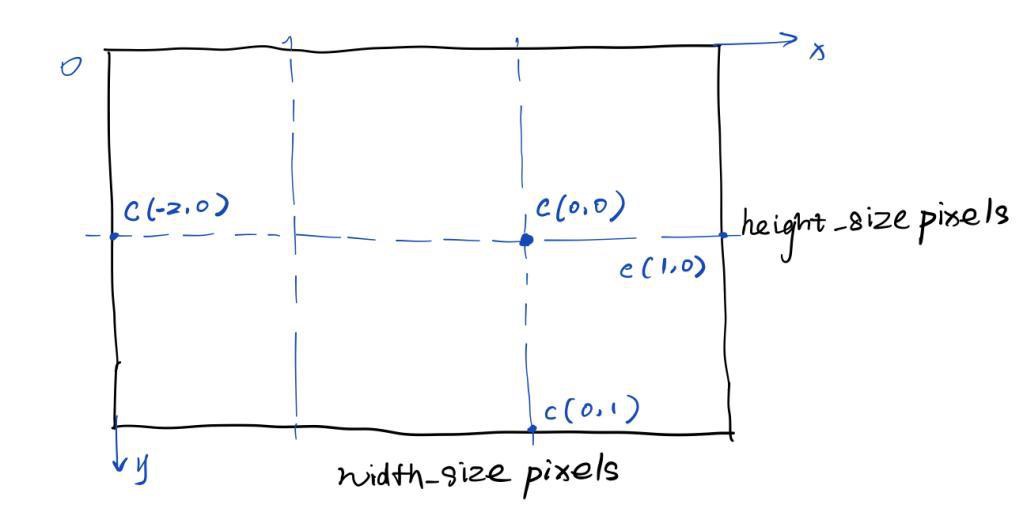
使用多进程并行，每个进程内使用多线程并行。

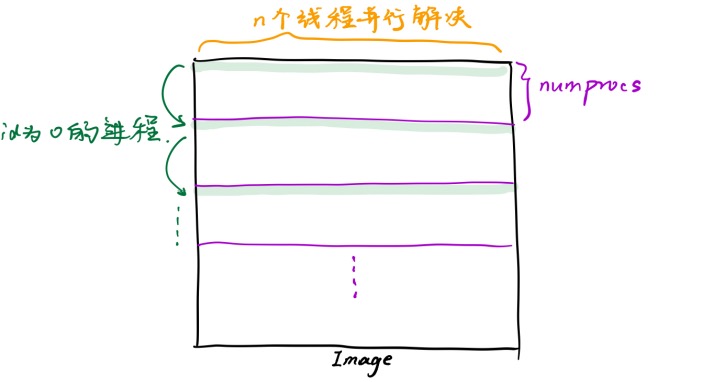
优化策略（2）：

利用集合的对称性质，进行对称优化。

计算效率探究实验

实验分为三部分：

（1）无对称优化和有对称优化下分别探究并行进程数、线程数的变化对计算效率的影响。

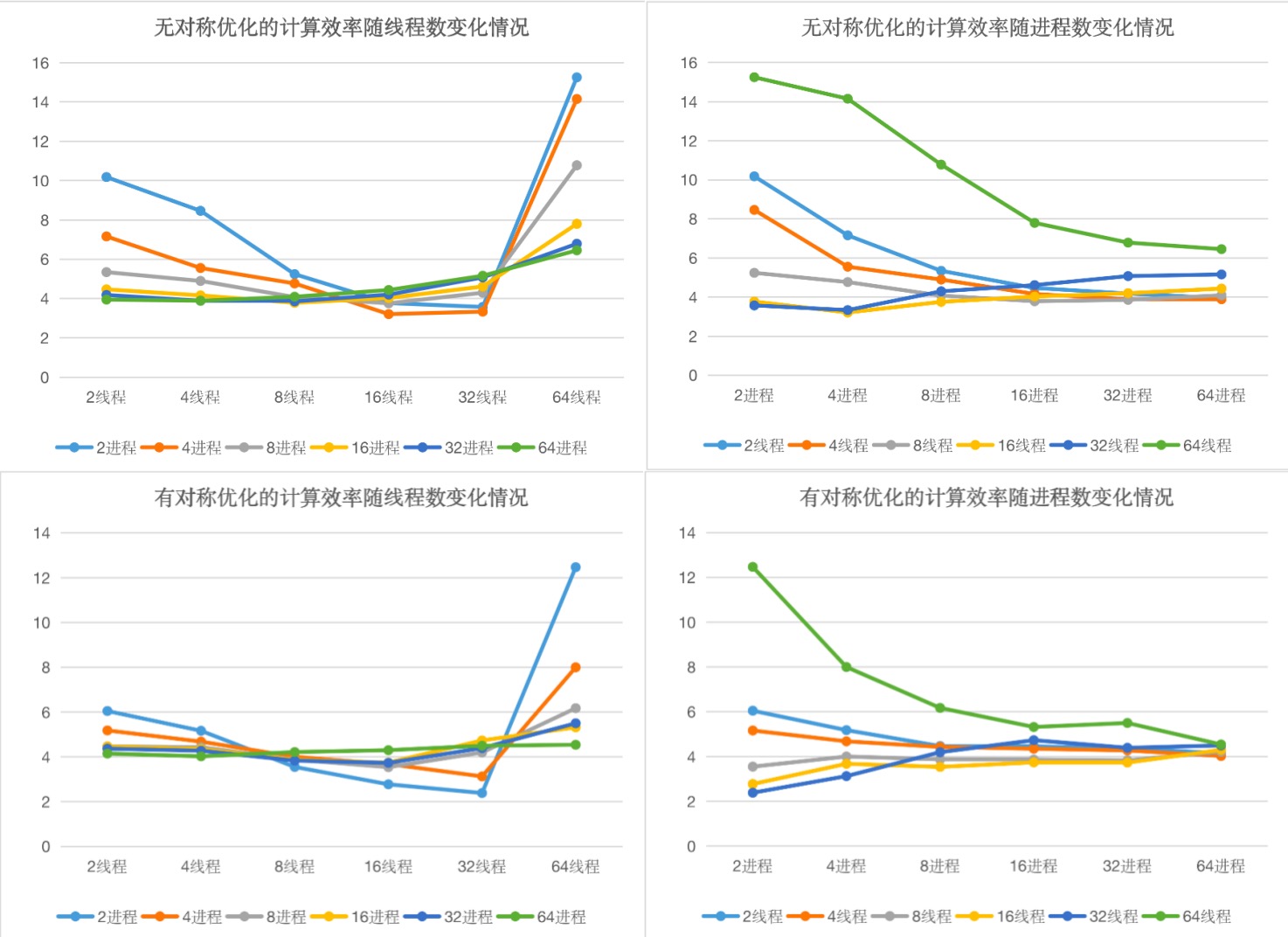
结论如下：

（1）在一定的并行进程数下，每个进程内的并行线程数不能一昧增加，受硬件资源CPU核数的限制，会存在一个能取得最好优化效果的最大并行线程数，这个值与当前的并行进程数相关，说明并行进程和并行线程二者占用的硬件资源是相互影响的，超过硬件资源限制的进程数或线程数请求都会起到反作用。

（2）在硬件资源限制内调用时，随着每个进程内并行线程数的增加，并行进程数的增加对计算时间消耗的优化效果越来越弱。

（3）与（2）对应的，随着并行进程数的增加，并行线程数的增加对计算时间消耗的影响越来越弱。

（4）通过实验数据来看，可以分析出每台机器在该数据规模下最多支持32线程并行达到效率最优，再增加调用的并行线程会起到反作用。

（5）线程更集中的情况下效率更优

（2）不同并行进程数、线程数下对称优化对计算效率的影响

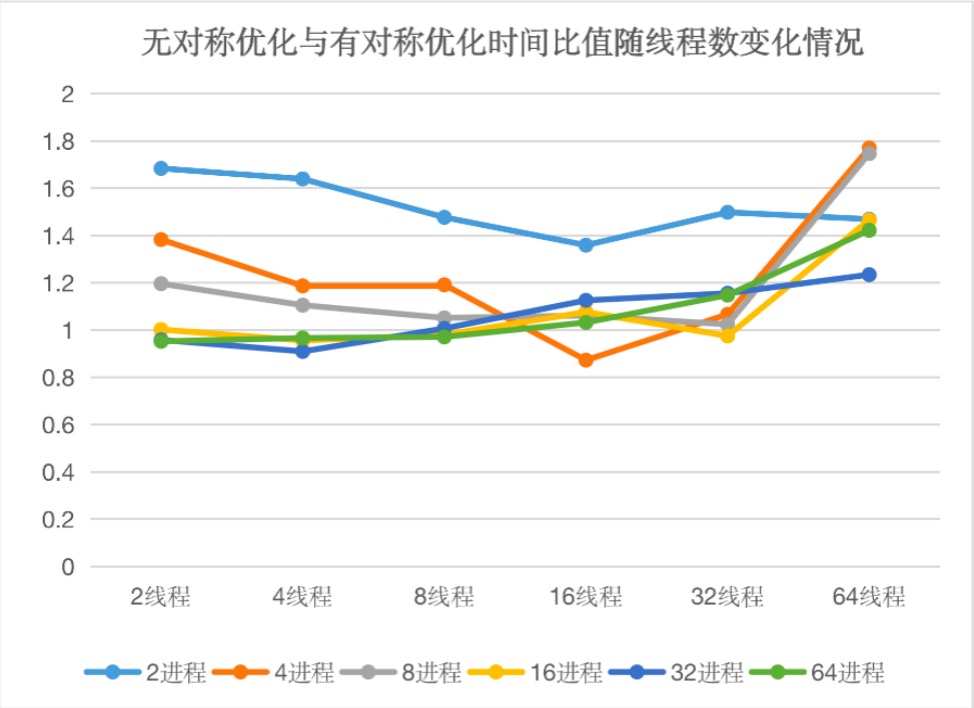
结论如下：

当硬件资源占用较少时数据规模对时间消耗的优化较大，但是当硬件资源占用比较紧张（没有超过资源限制）的情况下，数据规模对时间消耗的优化甚微，甚至有时还会起到副作用。这个原因我想是因为在硬件资源紧张时数据规模的减小会使得资源调度时间占并行计算时间的比例增加，从而导致优化效果不好。

（3）在并行优化最好的资源调用下，数据规模对计算效率的影响。

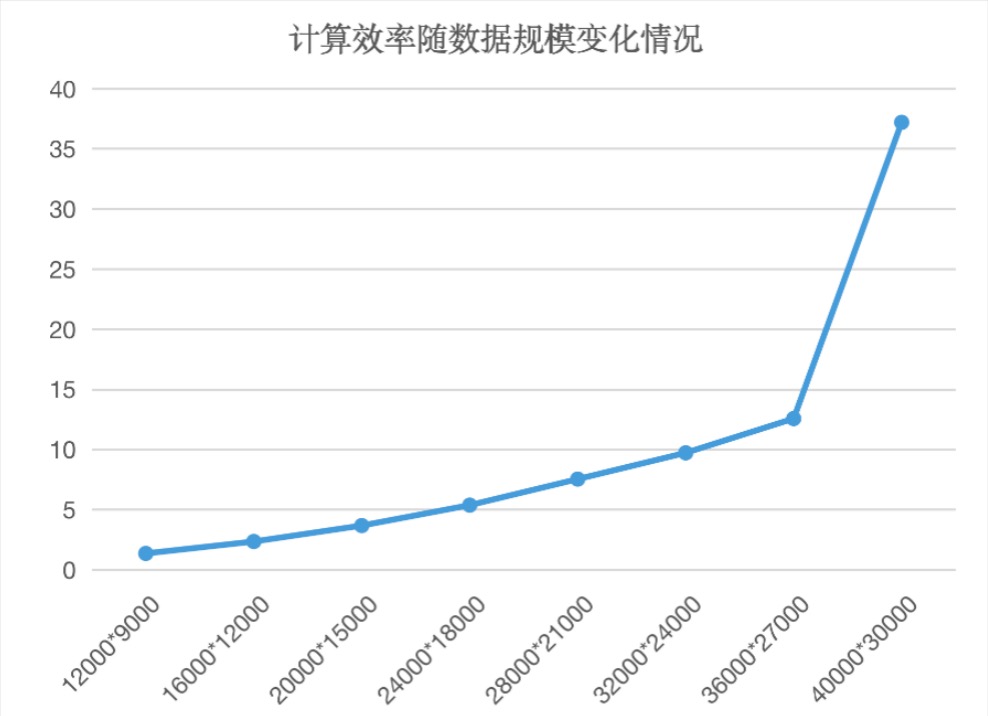
结论如下：

数据规模越大，计算的时间消耗增长越快。原因是当数据规模过大，会导致硬件资源的利用率达到最大，从而无法更多的发挥并行计算的优势。

实验输出结果

这里抛开性能不谈，观察随数据规模的增加，Mandelbrot Set图片分辨率的变化情况。

存在的问题

（1）硬件资源调度时间消耗与并行计算带来的效率提高二者间的平衡情况与数据规模的关系没有体现。

（2）在数据规模对计算效率的影响探究中，数据规模的选择有些不科学。