寒假集训思维训练4题解

A - A+B Again?
很简单 自己写

B - Card Game
分类讨论就行了
三种情况
1 第一个人赢两次
2 第一个人先赢再平局
3 第一个人先平局再赢
写好讨论就行了

C - Showering
题目意思就是给了$N$个时间段，题目比较贴心，他已经按时间线顺序给出的$N$个时间区间，问是否存在一个时间间隙满足$>=s$ 。直接枚举时间区间，计算两个相邻区间的时间差就行了$L[i]-R[i-1]$
计算第i个任务开始的时间与前一个任务结束的时间中间的时间间隙

#include<bits/stdc++.h>
using namespace std;
struct node{
	int l,r;
}a[200005];
int main(){
	int t;
	cin>>t;
	while(t--){
		bool ok=false;
		int n,s,m;
		cin>>n>>s>>m;
		a[n+1].l=m;
		a[0].r=0;
		for(int i=1;i<=n;i++){
			cin>>a[i].l>>a[i].r;
			if(a[i].l-a[i-1].r>=s&&!ok){
				cout<<"YES"<<'\n';
				ok=true;
			}
		}
		if(a[n+1].l-a[n].r>=s&&!ok){
			ok=true;
			cout<<"YES\n";
			continue;
		}
		if(!ok)cout<<"NO"<<'\n';
	}
	return 0;
}

D - Slavic’s Exam
首先要知道子序列的概念 以下是课堂一些笔记

给你两个字符串  S   T
	S只有小写字母以及   ?     ？是可以变为 小写字母   
	T 就是小写字母   
	
	题目想问  有没有方法使得? 变了之后 
	能够满足T是S的子序列   只要满足按顺序依次出现就行了  
	
	S:abcdefg 
	T:adg  
	T就是S的子序列   
	
	你可以枚举S    来从S当中  从前往后   依次匹配出T  
	
	
	abdae
    dac  
	
	S[1]->T[1]
    S[2]->T[1]
	S[3]->T[1]	
    S[4]->
    只需要枚举S字符串从前往后，依次尝试匹配T字符串，直到T字符串完全匹配出来      

答案代码

#include<bits/stdc++.h>
using namespace std;
char s[200010];
char t[200010];
int main()
{
	int T;
	cin>>T;
	while(T--){
		cin>>s+1;
		cin>>t+1;
		int n=strlen(s+1);
		int m=strlen(t+1);
		int pos=1;//目前想匹配的T字符串位置 
		for(int i=1;i<=n;i++){
			if(pos==m+1){//如果T字符串已经匹配好了 
				if(s[i]=='?')s[i]='a';//还遇到的? 随便改个字母  
				continue;	
			}
			if(s[i]=='?'){
				//如果现在是?  直接强行改为跟T[pos]匹配的字母就行了  
				s[i]=t[pos];
				pos++;//进入下一个T的匹配位置  
			}
			else if(s[i]==t[pos]){ // 如果一样  进入下一个匹配位置 
				pos++;
			}
		}
		if(pos==m+1){
			cout<<"YES"<<'\n';
			cout<<s+1<<'\n';
		}
		else{
			cout<<"NO"<<'\n';
		}
	}
	return 0;
}

E - Creating Words
太简单了

F - Maximum Multiple Sum
很简单，自己读题分析一下就知道怎么做了

G - Good Prefixes
首先要知道什么是前缀，前缀指的是某个数组从1号位置到$i$号位置 即$A[1--i]$

定义:  如果一个数组 存在一个元素的值 =  其余所有元素的和 那么数组就是好的 

题目问  给你一个数组A 
问有多少段A的前缀  :   A[1~i] 称之为A的前缀  
有多少段A的前缀，是好的

判断该数组的最大值  是否等于  其余的总和  


可以for 过去，依次算出A[1~i]的和，以及[1~i]区间的最大值

sum[i] 表示为A数组中前i个数的总和  

ma 表示前i个数中的最大值   
ma==sum[i]-ma   

int sum=0;
int ma=0;
int ans=0;
for(int i=1;i<=n;i++){
	int x;
	cin>>x;
	sum=sum+x;//计算前缀和
	if(ma<x)ma=x;//计算前缀 最大值
	if(ma==sum-ma)ans++;   
}   
这种写法是边计算前缀和，边计算前缀最大值   注意开long long 哦  

正确代码

#include<bits/stdc++.h>
using namespace std;

int main() {
	int t;
	cin>>t;
	while(t--){
		long long int n;
		cin>>n;
	    int cnt=0;
	    int ma=0;
	    long long int sum=0;
		for(int i=1;i<=n;i++){
			int x;
			cin>>x;
			sum=sum+x;
			if(x>ma)ma=x;
			if(sum-ma==ma)cnt++;
		
		}
		cout<<cnt<<endl;
	}
	return 0;
}

H - Manhattan Circle
其实，我们可以想一下，如果曼哈顿圆心所在的位置的那一行，水平方向肯定是直径，那么水平方向的#肯定也是最多的，同样的道理，竖着的方向也是#最多的。所以你找到横竖#最多的位置，就是圆心

但是这个题，$n\ast m<=2e5$ 。只能保证有$2e5$个字符，没保障行，列。如果你要开字符数组来存储矩阵，那么最坏需要$2e5行以及2e5列$ 很明显这样子的内存是开不出来的。所以有两个方法

方法1 输入的过程不存储矩阵，直接统计行，列的#数量，最后去枚举所有的行找到#最多的行号

#include<bits/stdc++.h>
using namespace std;
int H[200020];
int L[200020];
int main(){
	int t;
	cin>>t;
	while(t--){
		
	int n,m;
	cin>>n>>m;
	char op;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>op;
			if(op=='#'){
				H[i]++;//H[i]表示第i行的# 数量 
				L[j]++;	//L[j]表示第j列#的数量 
			}
				
		}
	}	
		int x,y;
		int Max=0;
		int May=0;
		for(int i=1;i<=n;i++){ //枚举n行  
			if(Max<H[i]){
				x=i;
				Max=H[i];
			}
			H[i]=0;//清空标记   
		}
		for(int i=1;i<=m;i++){ //枚举m列 
			if(May<L[i]){
				y=i;
				May=L[i];
			}
			L[i]=0;
		}
		cout<<x<<" "<<y<<'\n';
	}
	return 0;
}

方法2 使用string类型来存储字符串，因为string是不定长类型的字符串，所以能够巧妙地解决字符数组的空间问题，
string s 就表示一个字符串，如果要开二维，要写string s[10000] 其余思路还是统计行列的个数

#include<bits/stdc++.h>
using namespace std;
string a[200010];// string 是字符串类型   它可以输入不定长字符串
//起点是0 下标    
int main() {
	int t;
	cin>>t;
	while(t--) {
		int m,n;
		cin>>n>>m;
		for(int i=0; i<n; i++) {
			cin>>a[i];
		}
		int ma=0;

		int x=0;
		for(int i=0; i<n; i++) {
			int sum=0;
			for(int j=0; j<m; j++) {
				if(a[i][j]=='#') {
					sum++;
				}
			}
			if(sum>ma) {
				ma=sum;
				x=i;
			}
		}
		int ma2=0;
		int y=0;
		for(int i=0; i<m; i++) {
			int sum=0;
			for(int j=0; j<n; j++) {
				if(a[j][i]=='#') {
					sum++;
				}
			}
			if(sum>ma2) {
				ma2=sum;
				y=i;
			}
		}
		cout<<x+1<<' '<<y+1<<endl;
	}
	return 0;
}

I - Secret Box
这个题需要一定的三维空间基础。首先想一想平面上，一个面积为X的矩形，在给定的$N\ast M$的范围内有多少种可能位置呢?

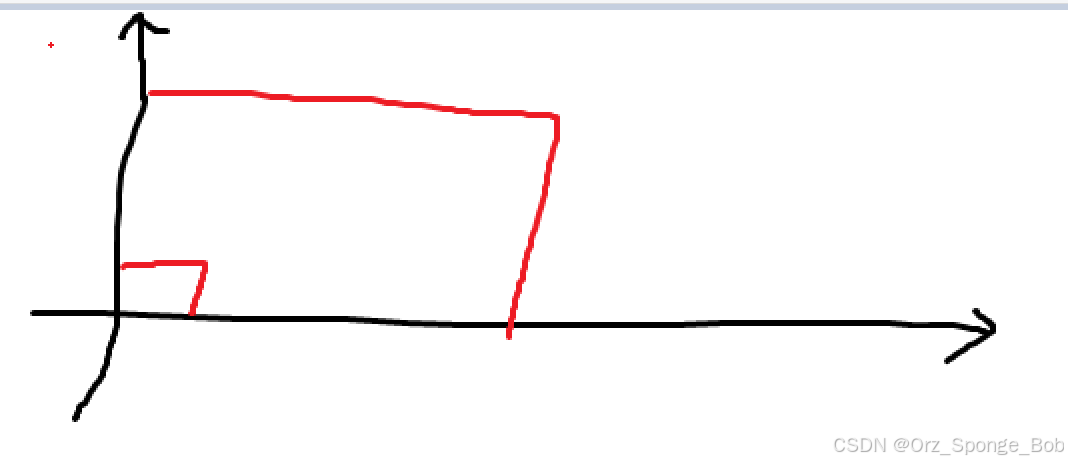
面积为$X$的矩形需要去枚举，因为边长为$a\ast b$，那么把某个矩形放到范围中来看，它其实可以通过平移的方式，去占据不同的位置。

那么X轴方向上至多可以挪动$0到N-a$ 个单位 ; Y轴方向上至多可以移动$0到M-b$个单位
总共$(N-a+1)\ast (M-b+1)$种不同的摆放方式，其中$a,b$也是需要枚举得到的，因为$a\ast b=X$
接下来我们来想一想三维空间中，限定一个盒子，限定物体的体积V，有多少种可能的方法?
我们可以先想象一下枚举立方体边长为$x\ast y\ast z$ 先去想象一下$x,y轴的情况，类似于二维空间$
至于你的$z$轴，其实也是类似于刚刚的计算方式

#include<bits/stdc++.h>
#define int long long
const int mod = 1e9 + 7;
using namespace std;

signed main()
{
	int t, x, y, z, k;
	cin >> t;
	while(t--){
		int ans = 0, cnt = 0;
		cin >> x >> y >> z >> k;
		for(int a = 1; a <= x; a++){
			for(int b = 1; b <= y; b++){
				if(k % (a * b) != 0 || k % (a * b) > z){
					continue;
				}
				int c = k / (a * b);
				cnt = (x - a + 1) * (y - b + 1) * (z - c + 1);
				ans = max(ans, cnt); 
			}
		} 
		cout << ans << endl;
	}
	return 0;
}