1.引言
手写数字是人手书写的各种字符中最简单常见的一种。在过去的30多年间,对手写数字识别的研究一直都是模式识别领域的研究热点。数字是世界各国通用的符号,类别也较少,有助于做深入分析及验证一些新的理论,因此它也是各种识别算法优劣的重要检测手段。手写数字识别的基本过程,一般可分为手写数字样本的收集、输入和预处理、特征提取、分类和识别等几个步骤。多年来,为了提高识别率和运行速度、降低误识率,众多的学者就纷纷识别的步骤提出各种新技术和新想法。大家讨论的焦点主要集中在特征提取、分类以及识别等方面。
手写数字识别(Handwritten Numeral Recognition)是光学字符识别技术(Optical Character Recogmition,简称OCR)的一个分支,它研究的对象是:如何利用电子计算机自动辨认人手写在纸张上的阿拉伯数字。随着社会信息化的发展,手写数字的识别研究有着重大的实用价值,如在邮政编码、税务报表、统计报表、财务报表、银行票据、海关、人口普查等需要处理大量字符信息录入的场合。
手写体数字识别方法大体可分为两类:基于统计的识别方法和基于结构的识别方法。第一类方法包括模板匹配法、矩法、笔道的点密度测试、字符轨迹法及数字变换法等。第二类则是尽量抽取数字的骨架或轮廓特征,如环路、端点、交叉点、弧状线、环及凹凸性等,两类方法具有一定的互补性。手写数字识别是当前图像处理和模式识别领域的一个重要研究分支,由于手写数字的随意性大,其识别准确率易受字体大小、笔画粗细和倾斜角度等因素的影响,因此进行手写数字识别方法和系统的设计具有重要的理论价值和实际意义。
手写体数字用多层BP网络来识别可以采用两种输入网络的形式:一种是点阵(0,1点阵)直接输入网络,利用网络来抽取特征并进行分类,这也叫点阵输入网络;另一种是通过一些算法,抽取字符特征,然后将一组特征值输入网络,利用神经网络对特征分类,达到识别字符的目的,这也叫作特征输入网络,它仅起分类作用。对于识别手写体数字,特征输入网络要比点阵输入网络效果好。
特征输入网络多数是直接输入提取的所有字符特征,一般来说,特征输入的越多识别才能越准确。但是太多的输入会使网络变的很大,难于收敛或者收敛到局部极小点。可以先对待识别数字进行粗特征分类,其作用是根据一些简单的特征对数字分类,选择具有这些简单特征的数字准备进行进一步识别;然后再提取其他特征,输入粗分类中选中的数字判别网络进行判别。
常用的特征提取方法,有逐像素特征提取法、骨架特征提取法和垂直方向数据统计特征提取法L6j等。逐像素特征提取法n3是一种最简单的特征提取方法,它是对图像进行逐行逐列地扫描,其特点是算法简单,运算速度快,可以使网络很快地收敛,训练效果好,但适应性不强;骨架特征提取法是一种利用细化的方法来提取骨架的方法。该方法对于线条粗细不同的数字有一定的适应性,但是图像一旦出现偏移就难以识别;垂直方向数据统计特征提取法就是自左向右对图像进行逐列地扫描,统计每列黑像素的个数,然后自上而下逐行扫描,统计每行的黑像素的个数,将统计结果作为字符的特征向量。这种方法的效果不是很理想,适应性不强。分类与识别的方式主要有贝叶斯分类器嘲、人工神经网络、多分类器组合或多级分类器、基于图论原理的分类、支持向量机等。由于人工神经网络具有自学习、容错性、分类能力强和并行处理等特点,因此它也是最常用的分类识别方式。在训练神经网络时最常用的是BP算法。由于手写体存在本身的不规则性及不同人书写风格的差异,手写数字的特征向量常出现交叉和混淆。可是BP网络采用剧变的判别边界来分割特征空间,对于样本特征空间存在交叉的情况,它将无法正确的估计出处于特征空间交叉处样本的隶属度值。不过,由于量子神经网络,具有超高速、超并行、指数容量级的特点,对具有不确定性、两类模式之间存在交叉数据的模式识别问题有极好的分类效果,因此,量子神经网络就可很好的克服常规BP神经网络的局限性。本文针对上述特征提取方法和BP神经网路的缺陷,提出了一种将新型特征提取方法(13维特征提取法)与量子神经网络相结合的手写数字识别方法。实验结果表明,与其他方法相比,该方法的识别正确率有了明显的提高。
3 全连接神经网络(DNN)
3.1全连接神经网络原理
全连接神经网络(DNN)是最朴素的神经网络,它的网络参数最多,计算量最大。
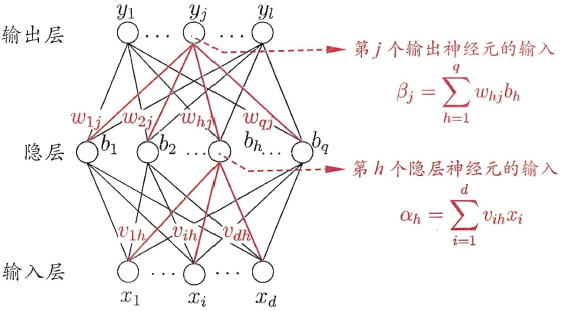
全连接神经网络规则如下:
-
神经元按照层来布局。最左边的层叫做输入层,负责接收输入数据;最右边的层叫输出层,我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层,因为它们对于外部来说是不可见的。
-
同一层的神经元之间没有连接。
-
第N层的每个神经元和第N-1层的所有神经元相连(这就是full connected的含义),第N-1层神经元的输出就是第N层神经元的输入。
-
每个连接都有一个权值。
DNN的结构不固定,一般神经网络包括输入层、隐藏层和输出层,一个DNN结构只有一个输入层,一个输出层,输入层和输出层之间的都是隐藏层。每一层神经网络有若干神经元,层与层之间神经元相互连接,层内神经元互不连接,而且下一层神经元连接上一层所有的神经元。
隐藏层比较多(>2)的神经网络叫做深度神经网络(DNN的网络层数不包括输入层),深度神经网络的表达力比浅层网络更强,一个仅有一个隐含层的神经网络就能拟合任何一个函数,但是它需要很多很多的神经元。
优点:由于DNN几乎可以拟合任何函数,所以DNN的非线性拟合能力非常强。往往深而窄的网络要更节约资源。
缺点:DNN不太容易训练,需要大量的数据,很多技巧才能训练好一个深层网络。
感知器
DNN也可以叫做多层感知器(MLP),DNN的网络结构太复杂,神经元数量太多,为了方便讲解我们设计一个最简单的DNN网络结构--感知机
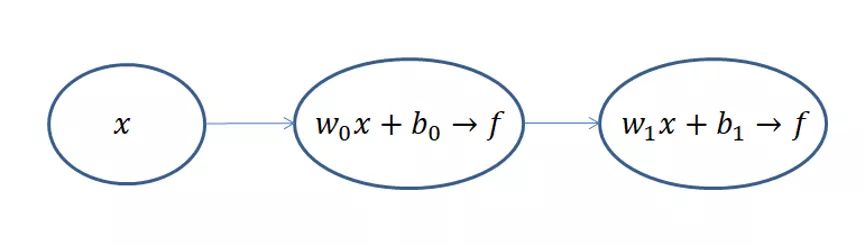
这是一个只有两层的神经网络,假定输入 x x x,我们规定隐层h和输出层o这两层都是 z = w x + b z=wx+b z=wx+b和 f ( z ) = 1 1 + e − z f(z)=\frac{1}{1+e^{-z}} f(z)=1+e−z1的组合,一旦输入样本x和标签y之后,模型就开始训练了。那么我们的问题就变成了求隐藏层的 w 0 、 b 0 w_0、b_0 w0、b0和输出层的 w 1 、 b 1 w_1、b_1 w1、b1四个参数的过程。
训练的目的是神经网络的输出和真实数据的输出"一样",但是在"一样"之前,模型输出和真实数据都是存在一定的差异,我们把这个"差异"作这样的一个参数 e e e代表误差的意思,那么模型输出加上误差之后就等于真实标签了,作: y = w x + b + e y=wx+b+e y=wx+b+e
当我们有n对 x x x和 y y y那么就有n个误差 e e e,我们试着把n个误差 e e e都加起来表示一个误差总量,为了不让残差正负抵消我们取平方或者取绝对值,本文取平方。这种误差我们称为“残差”,也就是模型的输出的结果和真实结果之间的差值。损失函数Loss还有一种称呼叫做“代价函数Cost”,残差表达式如下:
L o s s = ∑ i = 1 n e i 2 = ∑ i = 1 n ( y i − ( w x i + b ) ) 2 Loss=\sum_{i=1}^{n}e_i^2=\sum_{i=1}^{n}(y_i-(wx_i+b))^2 Loss=i=1∑nei2=i=1∑n(yi−(wxi+b))2
现在我们要做的就是找到一个比较好的w和b,使得整个Loss尽可能的小,越小说明我们训练出来的模型越好。
反向传播算法(BP)
BP算法主要有以下三个步骤 :
- 前向计算每个神经元的输出值;
- 反向计算每个神经元的误差项 e e e值;
- 最后用随机梯度下降算法迭代更新权重w和b。
我们把损失函数展开如下图所示,他的图形到底长什么样子呢?到底该怎么求他的最小值呢?
\begin{eqnarray}
Loss&=&\sum_{i=1}{n}(x_i2w2+b2+2x_iwb-2y_ib-2x_iy_iw+y_i^2)\
&=&Aw2+Bb2+Cwb+Db+Dw+Eb+F
\end{eqnarray}
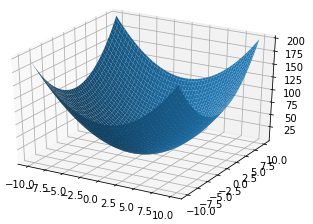
我们初始化一个 w 0 w_0 w0和 b 0 b_0 b0,带到Loss函数里面去,这个点( w o , b o , L o s s o w_o,b_o,Loss_o wo,bo,Losso)会出现在碗壁的某个位置,而我们的目标位置是碗底,那就慢慢的一点一点的往底部挪吧。
x n + 1 = x n − η d f ( x ) d x x_{n+1}=x_n-\eta \frac{df(x)}{dx} xn+1=xn−ηdxdf(x)
上式为梯度下降算法的公式,其中 d f ( x ) d x \frac{df(x)}{dx} dxdf(x)为梯度, η \eta η是学习率,也就是每次挪动的步长, η \eta η大每次迭代的脚步就大, η \eta η小每次迭代的脚步就小,我们只有取到合适的 η \eta η才能尽可能的接近最小值而不会因为步子太大越过了最小值。
当 x n = 3 x_n=3 xn=3时, − η d f ( x ) d x -\eta\frac{df(x)}{dx} −ηdxdf(x)为负数,更新后 x n + 1 x_{n+1} xn+1会减小;当 x n = − 3 x_n=-3 xn=−3时, − η d f ( x ) d x -\eta\frac{df(x)}{dx} −ηdxdf(x)为正数,更新后 x n + 1 x_{n+1} xn+1还是会减小。这总函数其实就是凸函数。满足 f ( x i + x 2 2 ) = f ( x i ) + f ( x 2 ) 2 f(\frac{x_i+x_2}{2})=\frac{f(x_i)+f(x_2)}{2} f(2xi+x2)=2f(xi)+f(x2)都是凸函数。沿着梯度的方向是下降最快的。
我们初始化 ( w 0 , b 0 , L o s s o ) (w_0,b_0,Loss_o) (w0,b0,Losso)后下一步就水到渠成了,
w 1 = w o − η ∂ L o s s ∂ w , b 1 = b o − η ∂ L o s s ∂ b w_1=w_o-\eta \frac{\partial Loss}{\partial w},b_1=b_o-\eta \frac{\partial Loss}{\partial b} w1=wo−η∂w∂Loss,b1=bo−η∂b∂Loss
有了梯度和学习率 η \eta η乘积之后,当这个点逐渐接近“碗底”的时候,偏导也随之下降,移动步伐也会慢慢变小,收敛会更为平缓,不会轻易出现“步子太大”而越过最低的情况。一轮一轮迭代,但损失值的变化趋于平稳时,模型的差不多就训练完成了。
梯度下降算法
我们用 w n e w = w o l d − η ∂ L o s s ∂ w w_{new}=w_{old}-\eta\frac{\partial Loss}{\partial w} wnew=wold−η∂w∂Loss讲以下梯度下降算法,零基础的读者可以仔细观看,有基础的请忽视梯度下降算法,我们定义y为真实值, y ^ \hat{y} y^为预测值
∂ L o s s ∂ w = ∂ ∂ w 1 2 ∑ i = 1 n ( y − y ^ ) 2 = 1 2 ∑ i = 1 n ∂ ∂ w ( y − y ^ ) 2 \frac{\partial Loss}{\partial w}=\frac{\partial}{\partial\mathrm{w}}\frac{1}{2}\sum_{i=1}^{n}(y-\hat{y})^2=\frac{1}{2}\sum_{i=1}^{n}\frac{\partial}{\partial\mathrm{w}}(y-\hat{y})^2 ∂w∂Loss=∂w∂21i=1∑n(y−y^)2=21i=1∑n∂w∂(y−y^)2
y是与 w w w无关的参数,而 y ^ = w x + b \hat{y}=wx+b y^=wx+b,下面我们用复合函数求导法
∂ L o s s ∂ w = ∂ L o s s ∂ y ^ ∂ y ^ ∂ w \frac{\partial Loss}{\partial\mathrm{w}}=\frac{\partial Loss}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial w} ∂w∂Loss=∂y^∂Loss∂w∂y^
分别计算上式等号右边的两个偏导数
∂ L o s s ∂ y ^ = ∂ ∂ y ^ ( y 2 − 2 y y ^ + y ^ 2 ) = − 2 y + 2 y ^ \frac{\partial Loss}{\partial\hat{y}}=\frac{\partial}{\partial \hat{y}}(y^2-2y\hat{y}+\hat{y}^2)=-2y+2\hat{y} ∂y^∂Loss=∂y^∂(y2−2yy^+y^2)=−2y+2y^
∂ y ^ ∂ w = ∂ ∂ w ( w x + b ) = x \frac{\partial \hat{y}}{\partial





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1269
1269


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?







