目录
NN4G(Neural network for Graph)
DCNN(Diffusion-Convolution Neural Network)
GIN(Graph Isomorphism Network)图同构网络
Introduction
GNN可以做什么
①Classification
解决分类问题,eg:input一个分子,经过一个分类器(classifier)输出1或者0,用来表示是否会发生突变。
②Generation
面对新冠疫情,生产新药,用一个generator来train出一些新的药分子,采用VAE变分自动编码器模型来解决就是,decoder一些新药物,输入给encoder的分子需要是一些简单的分子,能够比较容易合成新的分子。即GraphVAE

label不够,邻居来凑
如果我们不能给每个节点提供一个model,如何利用有限的label来train出一个好的模型,”近朱
者赤近墨者黑“,对于一个节点,它肯定和它相邻节点有特定的关系,我们可以利用这种特定的关系帮助model学习到node,如何用节点相邻的邻居帮助model做训练。

如何将节点嵌入到特征空间中使用
①将卷积的概念推广到图---->>spatial-based卷积
②回到信号处理中卷积的定义---->>Spectral-based卷积


GAT、GCN是比较常用的图卷积方式
Tasks,Dataset,and Benchmark

Spatial-based GNN
Aggregate:用neighbor feature update下一层的hidden state
Readout:把所有nodes的feature集合起来代表整个graph

NN4G(Neural network for Graph)
Aggregate:

Readout 
DCNN(Diffusion-Convolution Neural Network)

在上述这种情况下,叠加K层之后,就可以看到它的第K层neighborhood。
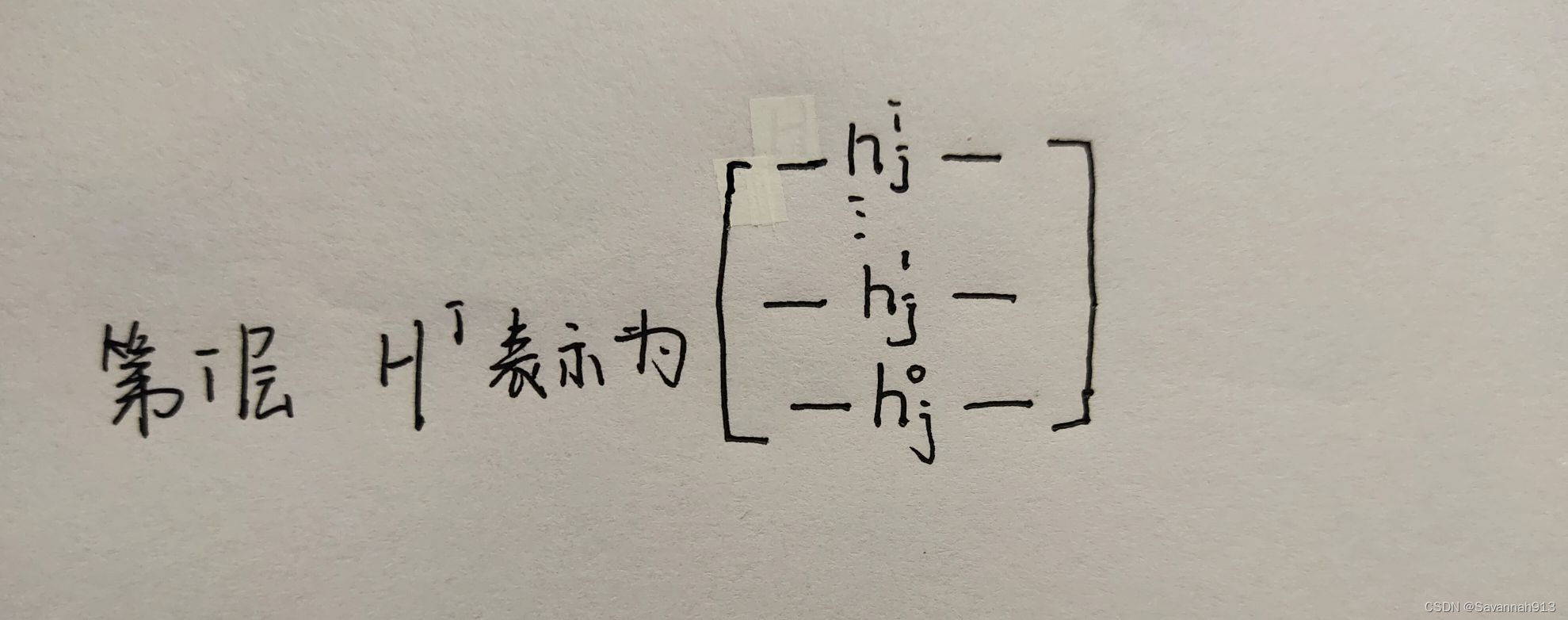

将所有节点都堆叠好之后第一列就是第一个节点与其邻域的关系,对每一列节点采取如下操作
或者:DGC(Diffusion Graph Convolution

MoNET(Mixture Model Network)
由于上述方法只是对某个节点所有邻居进行简单的相加,并没有顾及到哪个邻居节点更重要即权重的问题。可以通过定义节点间距离当做权重,用U(x,y)表示如下:

GraphSAGE
SAGE指的是 Sample and Aggregate,不是对每个顶点都训练一个单独的embeddding向量,而是训练了一组aggregator functions,这些函数学习如何从一个顶点的局部邻居聚合特征信息。
AGGREGATION:mean,max-pooling,or LSTM

对于LSTM操作,图邻居显然没有顺序,所以每次都是随机sample的顺序,每次都是不一样的,那么最终就会忽略顺序的影响。
GAT(Graph Attention Network)
对节点的邻居做attention操作

先求出对于中间节点来说,其他节点的重要程度,再根据其重要程度权重进行相乘相加。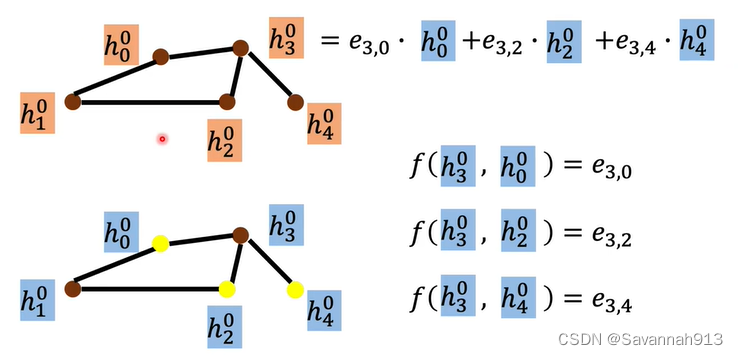
GIN(Graph Isomorphism Network)图同构网络
一个GNN最多可以像WL同构测试一样强大,对于节点v的同构方式

这里的计算最好用Sum比较容易区分不同的图

Spectral-Based Convolution

Signal and System
合成与分析
将一个信号看做n维空间的向量,

不同成分的线性组合,合成。求解每个部分是多少的时候就是进行分析。常用的basis是cos和sin这组basis,对于一个周期性的信号,可以将其展开为Fourier Series,选用的basis就是,不同的component大小就可以由
来决定,可以计算
的大小。
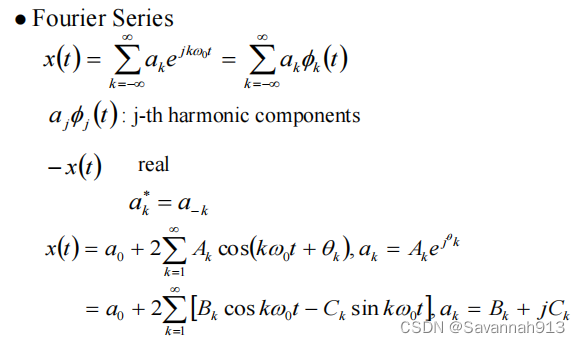
时间域与频率域

所以同一个信号,可以在时域和频率域中用两种不同的方式来合成。
频谱,频域傅里叶变换:

Spectral Graph Theory
符号定义:


拉普拉斯矩阵特点:对称矩阵、半正定矩阵、所有特征值都是大于等于0的数,可以对其进行正交分解,得到的λ是其频率frequency,u是与其相应的基。(L=D-A)



频率越大相邻两个信号点的变化就越大

理解vertex frequency

Lf的值表示了某个节点信号跟它旁边节点的信号差异,而真正看距离的话,需要对其平方,表示如下:f(vi)-f(vj)表示两个信号之间的差异,

节点间信号变化的能量(频率),图信号的平滑性,我们已经知道,频率越大,相邻两个信号之间的变化量就越大,而就是表示的信号间变化的频率,即

也就得正交化之后λ的值,即两两信号能量差距,λ小,信号之间差距就比较小,λ大,信号之间差距就比较大。如下图所示:
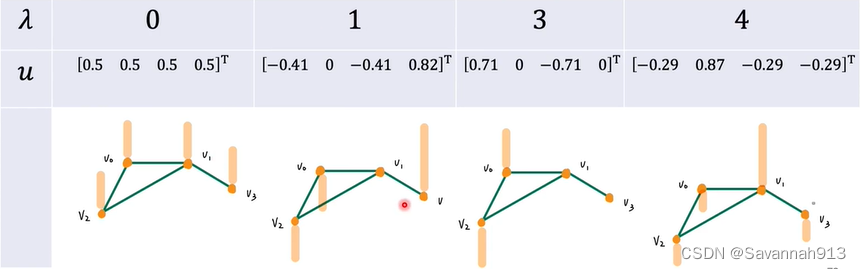
将信号从时域转换到频率域上
将一个图像从时域上通过傅里叶转换到频率域上如下图所示,那么如何通过傅里叶转换将一个图信号转换到频率域上表示呢

假设输入图的向量表示为X,通过乘以矩阵u来实现傅里叶转换,这个矩阵u就是由所有特征向量组成的特征矩阵,即频率λ所对应的向量。

这个向量乘以x做内积就得到了对应
对应的componen值
,如下图的
等等

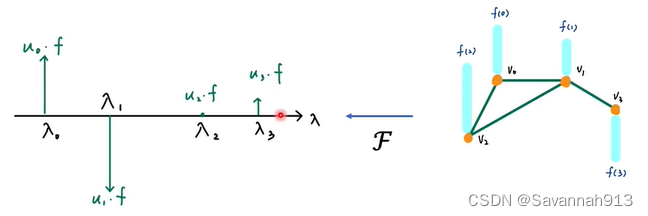
将信号从频率域转换到时域上
在图像上的转换如下图所示,根据各个基础图像所占的component即,以及图像的
,进行相乘相加计算,得到时域中的值x(t)

上述过程表现在图结构上:eg:对于节点0来说,就是每个特征向量中的节点0(如右侧所示)都要乘以频率域中特征向量对应的频率域中的表示再相加得到节点0对应时域中的值,其他节点也是这样计算,最终组成一个向量,该向量就是时域中该节点的表示。

过滤:修改信号中不同频率分量的幅值/相位,包括完全消除某些频率分量,频率整形、频率选择。下图所示,前两个图像的计算之后就得到过滤之后的信号情况(第三个图像)。

经过傅里叶转换之后的值乘以Fourier response,得到
,表现如下所示:
时域卷积就是频率域乘法!

最后一步得到在vector domain中的值y


想要train出一个model,这个model要做的就是给一个input为x,希望学到一个filter,叫做(
),经过filter之后可以得到y,所有要学的参数就是框起来的所有θ。但是要学习的参数的数量是和节点数相等的,所以,学习复杂度达到了O(n)。

还有一个问题就是,可能会学到原本不需要的特征。
下图中,如果这个过滤器得到的结果就是L,在图像上我们可以知道,节点0和节点3不是一阶邻居,没有直接相连,所以表现在拉普拉斯矩阵上,L(0,3)这个值就是0,与x相乘得到的y向量中的值就没有受到节点3的影响。

如果使得过滤器的结果是,那么,显然,每一个信号都会影响到y的每一个元素值。因为表现在图结构上,对于每一个节点,所有节点都能够通过两条边连到它,所以,每一个
矩阵中所有值都不是0。

举最极端的例子,使得所有节点都能分享到其他每一个节点的信号,那么这就是一种全局感受域了,我们想要做得是局部的,因为毕竟是图,相连的节点和不想连的节点的相关性还是差很多的。所以提出的K,即利用契比雪夫多项式的ChebNet图卷积,取L的k次方。
ChebNet
即能够提高运算速率(减少参数的学习个数),又能够专注于局部特征(最大到达k邻域)。

解决问题3就利用了切比雪夫多项式,切比雪夫多项式的x有约束条件。

将切比雪夫多项式应用到ChebNet卷积上,如下图所示:


就像下面这个例题一样,将原来的x转换成多项式x-2之后,在求第二问的时候就会容易很多,而第一问的参数也是我们需要学习的参数θ,即多项式系数。

那么原来的ChebNet模型就可以转换为:
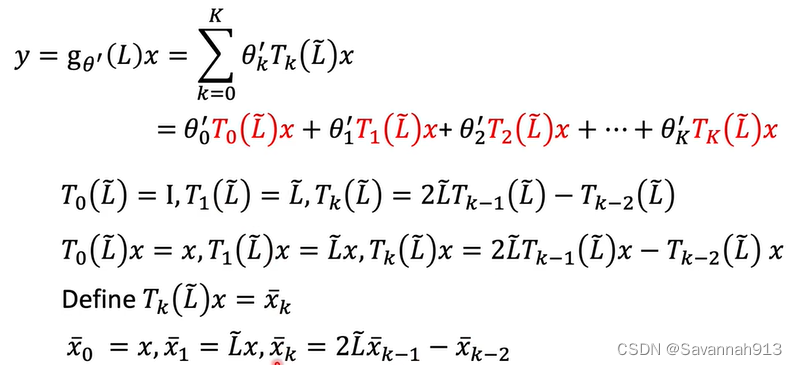

计算 是递归进行的, 而且,每次计算
的时间复杂度都是O(e),所以总的时间复杂度也大大降低了。
GCN
比较简单,比较直观。


GCN叠很多层的效果会更差一些,原因在于GCN的某些特性。解决方法:取平均时Drop掉一些节点。
VAE

GAN
AR-based model

























 2040
2040

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








