力扣热题100——双指针

双指针

• 两数之和（有序数组，相向双指针）
• 问题：在有序数组中找到两个数，使它们的和等于目标值。
• 思路：左指针从起点出发，右指针从终点出发，根据和与目标值的大小调整指针。

#include <vector>
using namespace std;

vector<int> twoSum(vector<int>& numbers, int target) {
    int left = 0;                  // 左指针（起点）
    int right = numbers.size() - 1; // 右指针（终点）
    
    while (left < right) {
        int sum = numbers[left] + numbers[right];
        
        if (sum == target) {
            // 找到目标，返回索引（题目可能要求+1，根据具体要求调整）
            return {left + 1, right + 1};
        } else if (sum < target) {
            // 和太小，左指针右移（增大总和）
            left++;
        } else {
            // 和太大，右指针左移（减小总和）
            right--;
        }
    }
    return {}; // 无结果（题目通常保证有解）
}

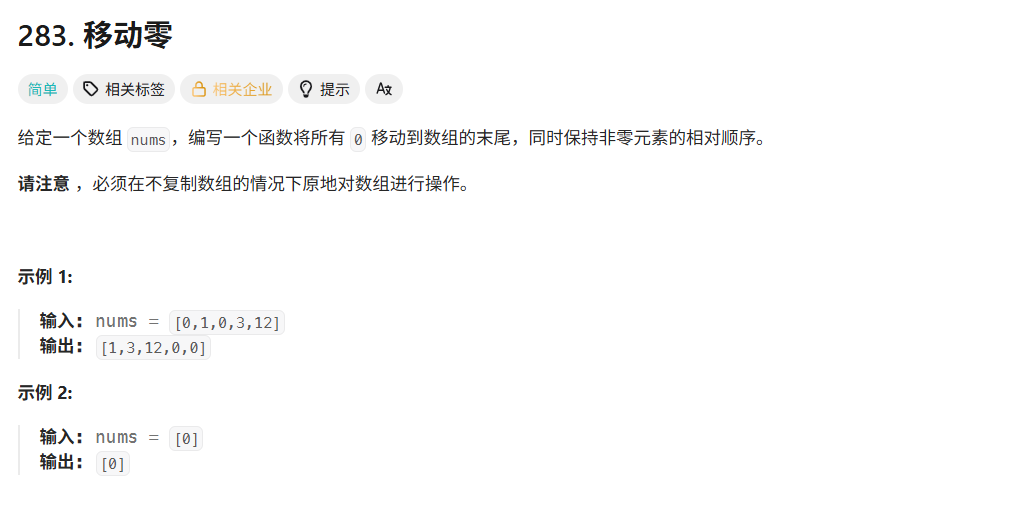
移动零

• 思路：左指针从起点出发，右指针也从起点出发，但是快慢不同。

class Solution {        // 定义Solution类，用于封装解题方法
public:                 // 公共成员函数，外部可直接调用
    // 函数定义：接收整数数组nums的引用（原地修改），无返回值
    void moveZeroes(vector<int>& nums) {
        
        int l = 0;      // 定义慢指针l，初始化为0
                        // 作用：记录下一个非零元素应该存放的位置
        
        int n = nums.size();  // 计算数组长度n，避免多次调用size()函数
        
        // 定义快指针r，从0开始遍历整个数组
        for(int r = 0; r < n; r++){
            
            // 当快指针指向的元素不是0时
            if(nums[r] != 0){
                
                // 将非零元素放到慢指针l的位置
                nums[l] = nums[r];
                
                // 慢指针后移一位，准备接收下一个非零元素
                l++;
            }
        }
        
        // 遍历结束后，慢指针l之前的位置已放满所有非零元素
        // 从l开始到数组末尾，填充0
        for(int i = l; i < n; i++){
            nums[i] = 0;
        }
        
    }
};

盛最多水的容器

class Solution {        // 定义Solution类，用于封装解题方法
public:                 // 公共成员函数，外部可直接调用
    // 函数定义：接收整数数组height的引用，返回最大容器容量（整数）
    int maxArea(vector<int>& height) {
        
        // 初始化双指针：left指向数组起点，right指向数组终点
        int left = 0, right = height.size() - 1;
        
        // 初始化最大容量为0，用于记录遍历过程中找到的最大容量
        int maxWater = 0;
        
        // 双指针循环条件：当左指针在右指针左侧时继续遍历
        while (left < right) {
            
            // 计算当前容器的高度：取左右指针所指高度的较小值（容器高度由矮边决定）
            int h = min(height[left], height[right]);
            
            // 计算当前容器的宽度：左右指针之间的距离（下标差）
            int w = right - left;
            
            // 更新最大容量：取当前容量（h*w）和历史最大容量的较大值
            maxWater = max(maxWater, h * w);
            
            // 指针移动策略：移动较矮一侧的指针（尝试寻找更高的边以增加容量）
            if (height[left] < height[right]) {
                left++;  // 左指针较矮，右移左指针
            } else {
                right--; // 右指针较矮（或等高），左移右指针
            }
        }
        
        // 循环结束后，返回最大容量
        return maxWater;
    }
};

三数之和

#include <vector>          // 引入vector容器头文件，用于存储动态数组
#include <algorithm>       // 引入algorithm头文件，用于调用sort排序函数
using namespace std;       // 使用std命名空间，简化代码书写

class Solution {           // 定义Solution类，封装解题方法
public:                    // 公共成员函数，外部可直接调用
    // 函数定义：接收整数数组nums，返回所有和为0的三元组（不重复）
    vector<vector<int>> threeSum(vector<int>& nums) {
        
        vector<vector<int>> res;  // 定义结果容器，存储符合条件的三元组
        
        sort(nums.begin(), nums.end());  // 对数组排序：1.便于双指针查找 2.便于去重
        int n = nums.size();       // 计算数组长度n，避免重复调用size()
        
        // 外层循环：固定三元组中的第一个元素nums[i]
        for (int i = 0; i < n; ++i) {
            
            // 去重：若当前元素与前一个元素相同，跳过（避免重复三元组）
            if (i > 0 && nums[i] == nums[i - 1]) continue;
            
            // 定义双指针：left指向i的下一个元素，right指向数组末尾
            int left = i + 1, right = n - 1;
            
            // 双指针循环：寻找与nums[i]之和为0的两个元素
            while (left < right) {
                
                // 计算当前三元组的和
                int sum = nums[i] + nums[left] + nums[right];
                
                if (sum == 0) {  // 找到和为0的三元组
                    // 将三元组加入结果容器
                    res.push_back({nums[i], nums[left], nums[right]});
                    
                    // 去重：跳过left指针的重复元素
                    while (left < right && nums[left] == nums[left + 1]) left++;
                    // 去重：跳过right指针的重复元素
                    while (left < right && nums[right] == nums[right - 1]) right--;
                    
                    // 双指针同时移动，继续寻找新的可能组合
                    left++;
                    right--;
                } 
                else if (sum < 0) {  // 和小于0，需增大总和（左指针右移）
                    left++;
                } 
                else {  // 和大于0，需减小总和（右指针左移）
                    right--;
                }
            }
        }
        
        return res;  // 返回所有符合条件的三元组
    }
};

接雨水

这个题目的关键是看每两个柱子之间的高度差，而不是相乘求面积！因为其中的数值有变化吗，如果按照求面积与盛水容器一样的方法就会导致多求！算错这是我的错误是思路！
但其相同点依旧是从左右指针开始判断大小。

 		int left = 0;
        int right = height.size() - 1;

        // 当左指针在右指针左侧时，继续遍历（两指针相遇则遍历结束）
        while (left < right) {......}

class Solution {
public:
    int trap(vector<int>& height) {
        // 左指针，初始指向数组最左端
        int left = 0;
        // 右指针，初始指向数组最右端
        int right = height.size() - 1;
        // 记录左侧已遍历区域的最高柱子高度
        int leftMax = 0;
        // 记录右侧已遍历区域的最高柱子高度
        int rightMax = 0;
        // 最终接雨水的总量
        int res = 0;

        // 当左指针在右指针左侧时，继续遍历（两指针相遇则遍历结束）
        while (left < right) {
            // 比较左右指针当前指向柱子的高度，优先处理较矮的一侧
            if (height[left] < height[right]) {
                // 左侧当前柱子高度 >= 左侧已记录的最高高度
                if (height[left] >= leftMax) {
                    // 更新左侧最高高度为当前柱子高度
                    leftMax = height[left];
                } else {
                    // 当前柱子可接雨水 = 左侧最高高度 - 当前柱子高度
                    res += leftMax - height[left];
                }
                // 左指针右移，处理下一个位置
                left++;
            } else {
                // 右侧当前柱子高度 >= 右侧已记录的最高高度
                if (height[right] >= rightMax) {
                    // 更新右侧最高高度为当前柱子高度
                    rightMax = height[right];
                } else {
                    // 当前柱子可接雨水 = 右侧最高高度 - 当前柱子高度
                    res += rightMax - height[right];
                }
                // 右指针左移，处理下一个位置
                right--;
            }
        }

        // 返回最终接雨水的总量
        return res;
    }
};