树状数组&&线段树

树状数组

树状数组就是一个可以是一个查询和修改复杂度都为log(n)的数据结构。为很多的查询和修改的速度提高了，减少的复杂度。
首先，我感觉很多人对这个的第一个理解肯定是树状应该是相互包含的一个样子，事实也是这样的。然后我看了很多的视频进行理解这个到底是什么样的东西，确实最后感觉有点像排列组合都是由规律的东西，而且很多公式只要记住好像就可以进行运用。

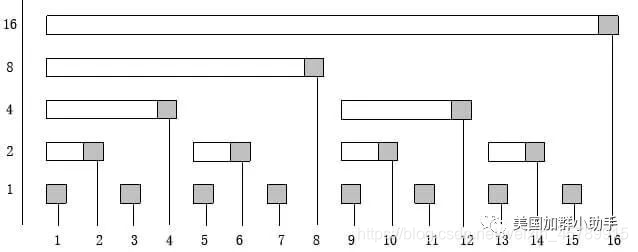
lowbit

int lowbit(int n)
{
  return n&(-n);
  }

这个就是找到二进制中最后一个1的位置
很多博客主都进行就讲解这个为什么是这样，然后进行理解一下就是。
10100 ——反码——01011——再在这个基础上加1——01100 取反末尾加1
注意：lowbit（0）=0，死循环。

修改：

对某个元素进行加法操作

void update(int x,int y)
{
		for(;x<=N;x+=lowbit(x))
		c[x]+=y;}

扩展

常用的代码：

int update(int x,int y,){
		int i=x，res=0；
		while(i>0)
		{ int j=y;
		while(j>0)
		{
			res+=c[i][j]
			j-=lowbit(j);
			    }
		i-=lowbit(i);
			}
	return res;
		}

int update(int x,int y,int z){
		int i=x;
		while(i<=n)
		{
		while(j<=m)
		{
			c[i][j]+=z;
			j+=lowbit(j);
			}
		i+=lowbit(i);
			}}

查询:

查询前缀的和

int sum(int x)
{
		int ans=0;
		for(;x=-lowbit(x)) ans+=c[x];
		return ans;
		}

统计a[x]…a[y]的和

在查询和的基础上最后调用sum的操作sum(y)-sum(x-1)

线段树

看了很多视频，都说只要是树状数组可以解决的线段树都可以解决，然后相比加来看线段树当然复杂一点。

看这个图片就很明显了，就是把一个个区间分成一个个小块，最后分到一个最具体的。所以首先最重要的就是找到左右的两个端点，才可以进行分。

初始建树（就是找 到范围左右点）

代码：

void bulid(int k,int l,int r)   //k表示当前结点的编号
{
	if(l==r)    //l左结点，r右结点
	{
	mi[k]=v;    //对应区间的最小值为原序列中的对应值
	return;
	}
	int mid=(l+r)/2;
	bulid(k*2,l,mid);   //左子树
	bulid(k*2+l,mid+1,r);    //右子树
	mi[k]=min(mi[k*2],mi[k*2+1]);   //自下向上更新
	}

询问：

区间进行询问操作

代码：

int query_min(int k,int l,int r,int x,int y)//x,y为询问区间，l，r为当前区间
{
	if(y<1||x>r) return ‘极大值’;
	if(x<=1&&r<=y) return mi[k];//询问区间在当前区间，返回一个极大值
	int mid=(l+r)/2;
	return min(query_min(k*2,l,mid,x,y),query_min(k*2+1,mid+1,r,x,y));
	}//否者分别处理左子区间和右子区间

修改：

单点修改：

void change(int k,int l,int r,int x,int v)//x为原序列位置，v为要改变的值
{
	if(r<x||l>x) return ;
	if(l==r&&l==x)
	{
	mi[k]=v;
	return ;
	}
	int mid(l+r)/2;
	change(k*2+1,mid+1,r,x,v);
	change(k*2,l,mid,x,v);
	mi[k]=min(mi[k*2],min[k2+1]);
	}