递归运算-1

递归运算

递归运算是运用有限的语句描述一个无穷的集合，并且递归的调用可以自身直接调用（直接递归调用），也可以其他函数进行调用（间接递归调用）

递归的运算的要领：

1. 找到终止条件！！！！（通常应该是第一个或者前几个做为）
2. 然后就根据题目缩小规模进行运算！！！

• 最简单例子—阶乘
  n!=1 * 2 * 3…*n

• 找到终止条件，当0！时等于1是最特别的，所以当n==1时为终止条件

• 然后注意观察此方程，是由每n和n-1项的乘机构成，所以其条件应该就是
  n *face（n-1）
  由图片可以明确的看出其调用方法以及返回。
  

所以我们就可以写出代码，这是一个简单的递归调用。

#include <iostream>
using namespace std;
long fact(int n)
{if(n==0) return 1;
else return n * fact(n-1)
}
int main()
{ 
	int n;
	cin>>n;
	cout<<fact(n)<<endl;
}

***全排列

如何将1234全排列呢？
也就是1可以在前面，然后234在后面进行排列。然后依次是2，3，4在第一位时后位进行排列的方法。
与之前一样，首先我们要找到终止条件

//产生从元素k-m的全排列，作为前k-1个元素的后缀
void perm(char list[],int k,int m)
{//构成一次全排列
    if(k==m)
    {
        for(int i=0;i<m;i++)
        cout<<list[i]<<" ";
        cout<<endl;
        }
        else
        for(int j=k;j<=m;j++)
    {
        swap(list[k],list[j]);//进行交换
        perm(list,k+1,m);//再次调用
        swap(list[k],list[j]);
        }
        }

swap就是简单的交换函数
要起到交换作用代码应该这样

void swap(int *a,int *b)
{  int temp;
   temp=*a;
   *a=*b;
   *b=temp;
}
int main ()
{  	int a=6,b=3;
	swap(&a,&b);
	return 0;
}

描述
给定一个由不同的小写字母组成的字符串，输出这个字符串的所有全排列。 我们假设对于小写字母有’a’ < ‘b’ < … < ‘y’ < ‘z’，而且给定的字符串中的字母已经按照从小到大的顺序排列。

			输入
	输入只有一行，是一个由不同的小写字母组成的字符串，已知字符串的长度在1到6之间。
	输出
	输出这个字符串的所有排列方式，每行一个排列。要求字母序比较小的排列在前面。字母序如下定义：

已知S = s1s2…sk , T = t1t2…tk，则S < T 等价于，存在p (1 <= p <= k)，使得
s1 = t1, s2 = t2, …, sp - 1 = tp - 1, sp < tp成立。

有关sort的使用可以找这里！
对题目的基本解法：并且sort的头文件是#include < algorithm >

#include<iostream>
#include<cmath>
#include<iomanip>
#include<algorithm>
#include<cstring>
using namespace std;
void cal(char [],int ,int)；
int main()
{
	char r[6];
	int num;
	cin>>r;
	num=strlen(r);//这是计算串长的
	sort(r,r+num);//先确定一个从小到大的排序顺序
	cal(r,0,num-1);
}
void cal(char r[6],int k,int m)//m为最后一个下标字符，第k位到m位
{	
	char s;
	if(k==m)//如果第k位等于第m位则可以直接输出
	cout<<r<<endl;
	else 
	for(int i=k;i<=m;i++)//应该是第k位带最后一位m的循环
	{s=r[i];r[i]=r[k];r[k]=s;//先确定最大的放在第一位进行交换
	sort(r+k+1,r+m+1);//然后后面进行排序
	cal(r,k+1,m);
	sort(r+k+1,r+m+1);//恢复原来的排序
	}
}

半数集问题

题目要求：



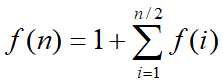
递归运算

int comp(int n)
{	int ans=1;
	if(n>1) for(int i=1;i<=n/2;i++)
	ans+=comp(i);
	return ans;
}

递归运算–记忆式搜索（无需从最开始再进行，已经进行保存）

int a[1001];//定义一个数组
int comp(int n)
{	int ans=1;
	if(a[n]>0)return a[n];
	for(int i=1;i<=n;i++)
	a[n]=ans;//保存结果
	return ans;
}

递归的总结

• 通过递归调用将整个问题层层分解成处理方法相似的子问题

• 通过回溯，按照递归关系将子问题的解整理成整个问题的解

• 分解子问题时，对当前问题由多种情况需要考虑，需要逐一进行枚举

• 递归关系可以是一个公式、也可能是一个前提条件

• 

    第一次发表   2020 03.04  22：48             wry