【论文笔记】G3R: Gradient Guided Generalizable Reconstruction

原文链接：https://arxiv.org/abs/2409.19405

摘要：大尺度3D场景重建对虚拟现实和仿真等应用来说有重要意义。现有的神经渲染方法（NeRF、3DGS）实现了对大场景的真实重建，但其逐场景优化的成本高、速度慢，且过拟合会带来大视角变换下的伪影。可泛化方法或大型重建模型速度很快，但主要对小场景或物体重建，且渲染质量较低。本文引入可泛化重建方法G3R，可对大场景预测高质量3D场景表达。本文提出学习重建网络，使用可微渲染的梯度反馈信号来迭代更新3D场景表达，将逐场景优化的真实性和数据驱动先验的前馈预测快速性结合起来。在城市驾驶和无人机数据集上的实验表明，G3R可跨场景泛化，并能以10x的速度实现相当于或超越3DGS的性能，且对大视角变化的鲁棒性更高。

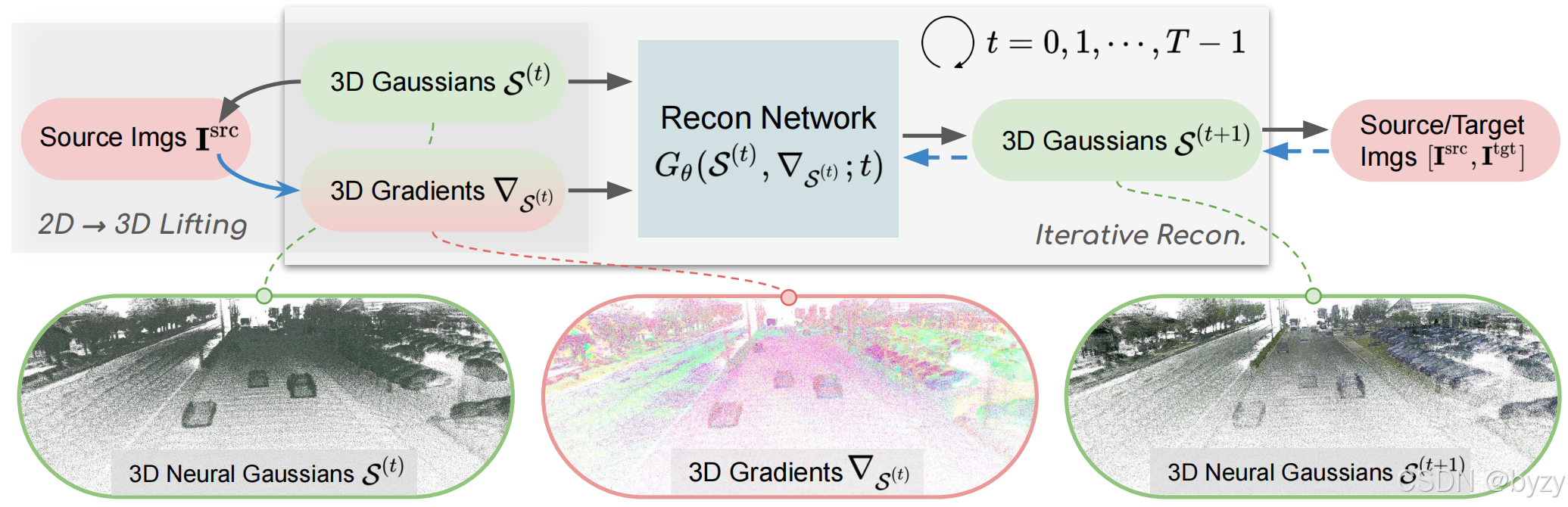
0. 梯度指导的可推广重建（G3R）概述

任务：给定大型动态场景中传感器移动平台捕捉的源图像集合 I s r c = { I i } 1 ≤ i ≤ N I^{src}=\{I_i\}_{1\leq i\leq N} Isrc={Ii​}1≤i≤N​和近似的几何脚手架$\mathcal{M}$（如激光雷达点或多视图立体中的点），目标是有效重建真实的、可编辑的3D表达$\mathcal{S}$，以进行实时摄像头仿真。

梯度指导的可推广重建（G3R）：G3R是第一个可在2分钟内建立大型真实场景的可修改数字克隆的方法，且可以>90FPS的速度生成真实度高的新视图。方法如图所示。G3R使用单一神经网络，迭代地更新由脚手架$\mathcal{M}$初始化的3D神经高斯表达。

1. G3R的场景表达

本文对3DGS进行了两种增强：首先为高斯表达增加一个隐式特征向量（称为3D神经高斯），从而为泛化重建和学习优化提供额外能力。其次，将场景分解为近处静态场景、动态参与者和远处区域，以建模无界动态场景。

3D神经高斯：本文的场景表达$\mathcal{S}$为3D神经高斯的集合，即 S = { h i } 1 ≤ i ≤ M \mathcal S=\{h_i\}_{1\leq i\leq M} S={hi​}1≤i≤M​，其中每个点由特征向量$h_i\in {\mathbb{R}}^C$表达。为了渲染，本文使用MLP将3D神经高斯转换为显式的3D高斯 G = { g i } 1 ≤ i ≤ M \mathcal G=\{g_i\}_{1\leq i\leq M} G={gi​}1≤i≤M​：$g_i=f_{mlp}(h_i)$。前14个通道被指定为3D高斯属性（位置、尺度、朝向、颜色和不透明度），并在$f_{mlp}$中添加跳跃连接。

刚性动态物体和无界场景的表达：3D神经高斯被分解为静态背景${\mathcal{S}}^B$，动态参与者${\mathcal{S}}^A$和远处区域${\mathcal{S}}^Y$。假设动态参与者进行刚体运动$\mathcal{T}({\mathcal{S}}^A,{\xi }^A)$，其中$\mathcal{T}$为刚体变换，${\xi }^A$为参与者外参。动态点${\mathcal{S}}^A$在不同帧间移动，使用3D边界框指示位置和大小。使用脚手架$\mathcal{M}$初始化静态背景和动态参与者的3D神经高斯，并固定一定数量的远处点以建模远处区域。

渲染：给定$\mathcal{S}$和相机姿态 Π = { K i , ξ i } \Pi=\{K_i,\xi_i\} Π={Ki​,ξi​}（其中$K_i$和${\xi }_i$为相机$i$的内外参），将$\mathcal{S}$转化为3D高斯$\mathcal{G}$后，使用可微tile栅格化器渲染图像$\hat{I}$：
$$\begin{array}{rl}{f}_{render}(\mathcal{S};\Pi )& :=f_{rast}(\mathcal{G};\Pi )=f_{rast}(f_{mlp}(\mathcal{S});\Pi )\\ & :=f_{rast}(f_{mlp}({\mathcal{S}}^B,{\mathcal{S}}^Y,\mathcal{T}({\mathcal{S}}^A,{\xi }^A));\Pi )\end{array}$$

2. 将2D图像提升为3D作为梯度

过去的泛化方法从源视图提取图像特征，并使用相机和几何先验（如对极几何或多视图立体）聚合之，从而将2D图像提升到3D。但每个图像分别由一个神经网络处理，受到存储限制，不能使用大量的输入图像来重建大型场景。

本文使用“渲染和反向传播”的方法将2D图像提升到3D，以获取3D表达的梯度。

优点：3D梯度作为统一表达，可有效聚合尽可能多的图像；3D梯度将渲染纳入考量，可自然处理遮挡；允许调整3D表达；3D梯度可通过现代可微栅格化引擎快速计算。

给定3D表达$\mathcal{S}$，首先渲染源视图图像${\hat{I}}_{src}=f_{render}(\mathcal{S};{\Pi }^{src})$，并与输入比较，计算重建损失$L$，并反向传播到3D表达$\mathcal{S}$以获得累积梯度${\nabla }_{\mathcal{S}}:={\nabla }_{\mathcal{S}}L(\mathcal{S},I^{src};{\Pi }^{src})$：
$$\begin{gathered} L(\mathcal{S},I^{src};{\Pi }^{src})=\sum _i\Vert I_i^{src}-{\hat{I}}_i^{src}{\Vert }_2=\sum _i\Vert I_i^{src}-f_{render}(\mathcal{S};{\Pi }_i^{src}){\Vert }_2 \\ {\nabla }_{\mathcal{S}}L(\mathcal{S},I^{src};{\Pi }^{src})=\frac{\partial L(\mathcal{S},I^{src};{\Pi }^{src})}{\partial \mathcal{S}}=\sum _i\frac{\partial \Vert I_i^{src}-f_{render}(\mathcal{S};{\Pi }_i^{src}){\Vert }_2}{\partial \mathcal{S}} \end{gathered}$$

其中可微函数$f_{render}$建立了2D到3D的联系；梯度${\nabla }_{\mathcal{S}}$以$\mathcal{S}$为代理，在3D中编码了2D图像。

3. 使用神经网络迭代重建

本节介绍如何给定源图像$I^{src}$，迭代更新场景表达$\mathcal{S}$。在每一步$t$，根据当前的3D表达${\mathcal{S}}^{(t)}$，通过可微渲染计算梯度${\nabla }_{{\mathcal{S}}^{(t)}}$，从而将2D源图像反投影到3D。随后，将${\nabla }_{{\mathcal{S}}^{(t)}}$送入网络$G_{\theta }$，预测更新的3D表达${\mathcal{S}}^{(t+1)}$：
$${\mathcal{S}}^{(t+1)}={\mathcal{S}}^{(t)}+\gamma (t)\cdot G_{\theta }({\mathcal{S}}^{(t)},{\nabla }_{{\mathcal{S}}^{(t)}}L({\mathcal{S}}^{(t)},I^{src};{\Pi }^{src});t)，t=0,1,\cdots ,T-1$$

其中$\gamma (t)$定义更新尺度。类似梯度下降，期望的衰减调度$\gamma (t)$和较小的$T$，使模型能预测初始的粗糙表达，并快速细化。本文使用DDIM中的余弦调度，并使用带稀疏卷积的3D UNet作为$G_{\theta }$。迭代过程使得3D表达能够被细化从而提高质量，同时能够使用更高效、更容易学习的小网络。

4. 训练 & 推断

对每个场景，从几何脚手架$\mathcal{M}$初始化场景表达${\mathcal{S}}^{(0)}$，并进行$T$步迭代细化。为增强泛化性，本文在训练时对源视图$I^{src}$和新视图$I^{tgt}$均进行了渲染，并传播梯度到$G_{\theta }$和$f_{mlp}$（注意$G_{\theta }$的更新只使用源视图的梯度）。对模型进行跨场景训练，总的损失为
$$L=L_{mse}(\hat{I},I)+{\lambda }_{lpips}{L}_{lpips}(\hat{I},I)+{\lambda }_{reg}{L}_{reg}(\mathcal{G})$$

其中$L_{mse}$为光度损失，$L_{lpips}$为感知损失，$L_{reg}$为正则化损失（使高斯$\mathcal{G}$扁平化以和表面对齐）：
$$L_{reg}(\mathcal{G})=\sum _i\max (0,d_i^{\min }-ϵ)$$

其中$d_i^{\min }$是高斯$g_i$ 3尺度中的最小值。

推断：给定预训练重建网络$G_{\theta }$和神经高斯解码器$f_{MLP}$，可重建新场景。输入新场景图像$I^{src}$和3D高斯初始化${\mathcal{S}}^{(0)}$，迭代计算梯度${\nabla }_{\mathcal{S}}$，细化3D表达。最后，将${\mathcal{S}}^{(T)}$转化为标准3D高斯${\mathcal{G}}^{(T)}$以进行实时栅格化。

实施细节：使用下采样的激光雷达点作为初始化高斯${\mathcal{S}}^{(0)}$的位置；高斯尺度被初始化为各向同性的，为第三近的点的距离。旋转被初始化为identity，不透明度被初始化为0.7。其它维度被随机初始化。未使用3DGS中的球面谐波。3D梯度${\nabla }_{{\mathcal{S}}^{(t)}}L({\mathcal{S}}^{(t)})$在输入网络前，被跨点逐通道归一化。动态场景为静态背景、动态参与者和远处区域使用3个网络，输出层使用tanh激活函数。逐场景重建步数$T=24$。
泛化能力：G3R能跨数据集泛化，即在A数据集上训练的模型，在B数据集上测试，可超过其它直接在B数据集上训练的方法的性能；若进一步在B数据集上使用少量数据微调，可达到与直接在B数据集上训练的G3R相当性能。

看上去本文方法是两步训练，第一步训练具有泛化能力的网络$G_{\theta },f_{mlp}$，第二步是逐场景训练高斯$\mathcal{S}$（速度较快）。此外，和传统3DGS不同，本文方法好像不能在训练过程中改变（静态）高斯数量（当然应该可结合进来，但速度会受到影响）。