- 数据聚类
图像分类 - 高斯混合模型(GMM)
高斯分布与概率密度分布(PDF)
初始化 - 跟K-Means相比较,属于软分类(随机概率)
实现方法:期望最大化(E-M)
停止条件:收敛 - 样本数据训练与预言
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace std;
using namespace cv;
using namespace cv::ml;
int main(int argc, char** argv)
{
Mat src(500, 500, CV_8UC3);
RNG rng;
const int MAX_CLUSTERS = 5;
Scalar color[] =
{
Scalar(0,0,255),
Scalar(0,255,0),
Scalar(255,0,0),
Scalar(0,255,255),
Scalar(255,0,255),
};
int clusterCount = rng.uniform(2, MAX_CLUSTERS);
cout << "number of clusters聚类数目 :" << clusterCount << endl;
int sampleCount = rng.uniform(5, 1001);
cout << "number of sampleCount采样点数目 :" << sampleCount << endl;
Mat points(sampleCount, 2, CV_32FC1);
Mat labels;
for (int i = 0; i < clusterCount; i++)
{
Point center;
center.x = rng.uniform(0, src.cols);
center.y = rng.uniform(0, src.rows);
Mat pointChunk = points.rowRange(i * sampleCount / clusterCount,
i == clusterCount - 1 ? sampleCount : (i + 1)*sampleCount / clusterCount);
rng.fill(pointChunk, RNG::NORMAL, Scalar(center.x, center.y), Scalar(src.cols*0.05, src.rows*0.05));
}
randShuffle(points, 1, &rng);
Ptr<EM> em_model = EM::create();
em_model->setClustersNumber(clusterCount);
em_model->setCovarianceMatrixType(EM::COV_MAT_SPHERICAL);
em_model->setTermCriteria(TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 100, 0.1));
em_model->trainEM(points,
noArray(),
labels,
noArray());
Mat sample(1, 2, CV_32FC1);
for (int row = 0; row < src.rows; row++)
{
for (int col = 0; col < src.cols; col++)
{
sample.at<float>(0) = (float)col;
sample.at<float>(1) = (float)row;
int response = cvRound(em_model->predict2(sample, noArray())[1]);
Scalar c = color[response];
circle(src, Point(col, row), 1, c*0.75, -1);
}
}
for (int i = 0; i < sampleCount; i++)
{
Point p(cvRound(points.at<float>(i, 0)), points.at<float>(i, 1));
circle(src, p, 1, color[labels.at<int>(i)], -1);
}
imshow("高斯混合模型EM", src);
waitKey(0);
return 0;
}
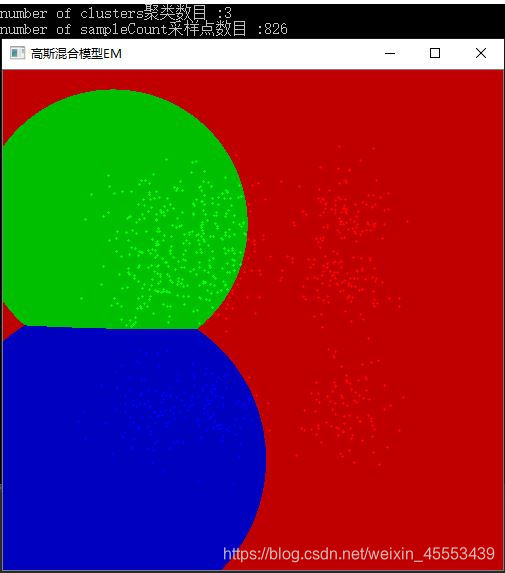











 这篇博客探讨了如何使用OpenCV进行图像分割,重点在于高斯混合模型(GMM)的数据分类。介绍了GMM的原理,包括高斯分布和概率密度分布,以及它与K-Means的区别——GMM采用软分类。文章还详细阐述了GMM的期望最大化(E-M)实现方法和停止条件,并讨论了模型的训练和预测过程。
这篇博客探讨了如何使用OpenCV进行图像分割,重点在于高斯混合模型(GMM)的数据分类。介绍了GMM的原理,包括高斯分布和概率密度分布,以及它与K-Means的区别——GMM采用软分类。文章还详细阐述了GMM的期望最大化(E-M)实现方法和停止条件,并讨论了模型的训练和预测过程。
















 1377
1377

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








