粒子群优化算法matlab

1.粒子群算法介绍

1.1发展概况

粒子群算法是在1995年由Eberhart博士和Kennedy博士一起提出的，它源于对鸟群捕食行为的研究。它的基本核心是利用群体中的个体对信息的共享从而使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的最优解。设想这么一个场景：一群鸟进行觅食，而远处有一片玉米地，所有的鸟都不知道玉米地到底在哪里，但是它们知道自己当前的位置距离玉米地有多远。那么找到玉米地的最佳策略，也是最简单有效的策略就是搜寻目前距离玉米地最近的鸟群的周围区域。

1.2算法原理

在PSO中，每个优化问题的解都是搜索空间中的一只鸟，称之为"粒子"，而问题的最优解就对应于鸟群中寻找的"玉米地"。所有的粒子都具有一个位置向量（粒子在解空间的位置）和速度向量（决定下次飞行的方向和速度），并可以根据目标函数来计算当前的所在位置的适应值（fitness value）,可以将其理解为距离"玉米地"的距离。在每次的迭代中，种群中的例子除了根据自身的经（历史位置）进行学习以外，还可以根据种群中最优粒子的"经验"来学习，从而确定下一次迭代时需要如何调整和改变飞行的方向和速度。就这样逐步迭代，最终整个种群的例子就会逐步趋于最优解。

2.算法流程

step1
种群初始化，可以进行随机初始化或者根据被优化的问题设计特定的初始化方法，然后计算个体的适应值，从而选择出个体的局部最优位置向量和种群的全局最优位置向量。

step2
迭代设置：设置迭代次数

step3
速度更新：更新每个个体的速度向量

step4
位置更新：更新每个个体的位置向量

step5
局部位置和全局位置向量更新：更新每个个体的局部最优解和种群的全局最优解

step6
终止条件判断：判断迭代次数时都达到最大迭代次数，如果满足，输出全局最优解，否则继续进行迭代，跳转至step 3。

2.1算法流程图

3.MATLAB实现

3.1代码

PSO.m

%% 清空环境
clc
clear

%% 参数初始化
%粒子群算法中的三个参数
c1 = 1.49445;%加速因子
c2 = 1.49445;
w=0.8   %惯性权重
w2=0.4
maxgen=1000;   % 进化次s数  
sizepop=200;   %种群规模

Vmax=1;       %限制速度围
Vmin=-1;     
popmax=5;     %变量取值范围
popmin=-5;
dim=10;       %适应度函数维数

func=1;       %选择待优化的函数，1为Rastrigin,2为Schaffer,3为Griewank
Drawfunc(func);%画出待优化的函数，只画出二维情况作为可视化输出

%% 产生初始粒子和速度
for i=1:sizepop
    %随机产生一个种群
    pop(i,:)=popmax*rands(1,dim);    %初始种群
    V(i,:)=Vmax*rands(1,dim);             %初始化速度
                                     %计算适应度
    fitness(i)=fun(pop(i,:),func);   %粒子的适应度
end

%% 个体极值和群体极值
[bestfitness bestindex]=min(fitness);
gbest=pop(bestindex,:);   %全局最佳
pbest=pop;                %个体最佳
fitnesspbest=fitness;     %个体最佳适应度值
fitnessgbest=bestfitness; %全局最佳适应度值

%% 迭代寻优
for i=1:maxgen
    fprintf('第%d代，',i);
    fprintf('最优适应度%f\n',fitnessgbest);
    w=w+(w2-w)/maxgen;
    for j=1:sizepop
        %速度更新
        V(j,:) = w*V(j,:) + c1*rand*(pbest(j,:) - pop(j,:)) + c2*rand*(gbest - pop(j,:)); %根据个体最优pbest和群体最优gbest计算下一时刻速度
        V(j,find(V(j,:)>Vmax))=Vmax;   %限制速度不能太大
        V(j,find(V(j,:)<Vmin))=Vmin;
        
        %种群更新
        pop(j,:)=pop(j,:)+0.5*V(j,:);       %位置更新
        pop(j,find(pop(j,:)>popmax))=popmax;%坐标不能超出范围
        pop(j,find(pop(j,:)<popmin))=popmin;
        
        if rand>0.98                         %加入变异种子，用于跳出局部最优值
            pop(j,:)=rands(1,dim);
        end
        
        %更新第j个粒子的适应度值
        fitness(j)=fun(pop(j,:),func); 
   
    end
    
    for j=1:sizepop
        
        %个体最优更新
        if fitness(j) < fitnesspbest(j)
            pbest(j,:) = pop(j,:);
            fitnesspbest(j) = fitness(j);
        end
        
        %群体最优更新
        if fitness(j) < fitnessgbest
            gbest = pop(j,:);
            fitnessgbest = fitness(j);
        end
    end 
    yy(i)=fitnessgbest;    
        
end
%% 结果分析
figure;
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);

Rastrigin.m

function y = Rastrigin(x)
% Rastrigin函数
% 输入x,给出相应的y值,在x = ( 0 , 0 ,…, 0 )处有全局极小点0.
% 编制人：
% 编制日期：
[row,col] = size(x);
if  row > 1 
    error( ' 输入的参数错误 ' );
end
y =sum(x.^2-10*cos(2*pi*x)+10);
%y =-y;

Schaffer.m

function y=Schaffer(x)

[row,col]=size(x);
if row>1
    error('输入的参数错误');
end
y1=x(1,1);
y2=x(1,2);
temp=y1^2+y2^2;
y=0.5-(sin(sqrt(temp))^2-0.5)/(1+0.001*temp)^2;
y=-y;

Griewank.m

function y=Griewank(x)
%Griewan函数
%输入x,给出相应的y值,在x=(0,0,…,0)处有全局极小点0.
%编制人：
%编制日期：
[row,col]=size(x);
if row>1
    error('输入的参数错误');
end
y1=1/4000*sum(x.^2);
y2=1;
for h=1:col
    y2=y2*cos(x(h)/sqrt(h));
end
y=y1-y2+1;
%y=-y;

fun.m

function y = fun(x,label)
%函数用于计算粒子适应度值
%x           input           输入粒子 
%y           output          粒子适应度值 
if label==1
    y=Rastrigin(x);
elseif label==2
    y=Schaffer(x);
else
    y= Griewank(x);
end

Drawfunc.m

function Drawfunc(label)

x=-5:0.05:5;%41列的向量
if label==1
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) = Rastrigin([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end

if label==2
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) = Schaffer([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp 
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end

if label==3
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) = Griewank([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp 
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end

3.2实验结果分析

3.2.1待优化函数：Rastrigin

①基于种群规模和进化次数修改对优化函数的影响

📊种群规模：500，进化次数：1000，实验次数：10次

最优适应度截图：

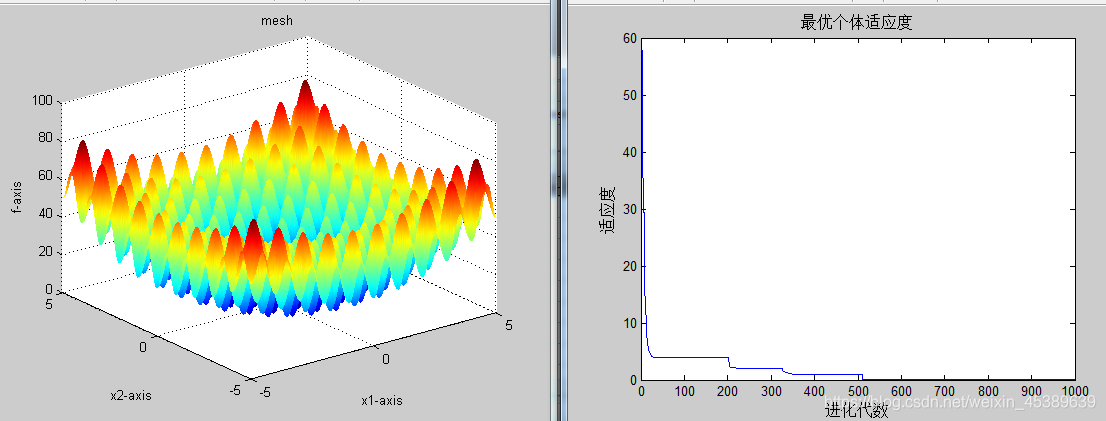
📊种群规模：200，进化次数：1000，实验次数：10次

最优适应度截图：

📊种群规模：200，进化次数：500，实验次数：10次

最优适应度截图：

📊种群规模：200，进化次数：1500，实验次数：10次

最优适应度截图：


结论：种群规模以及进化次数都不应过大或过小，两个影响着影响着算法的搜索能力和计算量，种群规规模过小，算法收敛速度快，但是容易陷入局部最优；导致很难迭代到最优适应度，同时增加了运行时间，进化次数的增加会降低种群的多样性所以不易过大过小。所以本实验取进化次数1000次，种群规模200

②基于加速因子 C2 和 C2 修改对优化函数的影响

📊加速因子C1:1.9 C2:1.4 种群规模：200，进化次数：1000，实验次数：10次

最优适应度截图

📊加速因子C1:1.5 C2:1.4 种群规模：200，进化次数：1000，实验次数：10次

最优适应度截图

![在这里插入图片描述](https://img-blog.csdnimg.cn/20191203230651675.pn

📊加速因子C1:1.5 C2:1.6 种群规模：200，进化次数：1000，实验次数：10次

最优适应度截图


结论：随着多次对算法的运算和数据的统计，设置c1较大的值，会使微粒过多地在局部范围内徘徊，而较大的c2的值，则又会促使微粒过早收敛到局部最小值。经过多次实验本实验取c1:1.3 c2:1.4

③基于惯性权值W以及加速因子 C2 和 C2 修改对优化函数的影响

w=w+(w2-w)/maxgen;

📊最大权重0.9 最小权重0.4 加速因子 C1:1.3 C2:1.4 种群规模：200，进化次数：1000，实验次数：10次

最优适应度截图

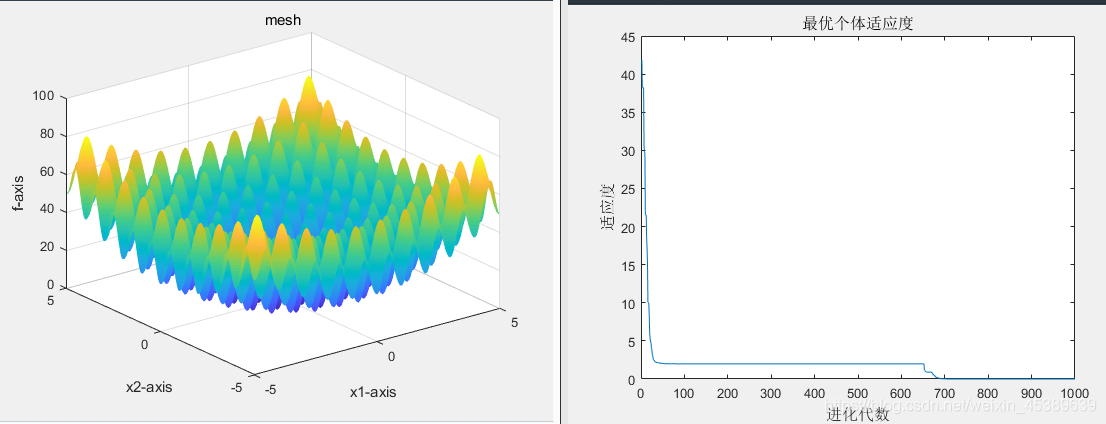
📊最大权重0.8 最小权重0.3 加速因子 C1:1.3 C2:1.4 种群规模：200，进化次数：1000，实验次数：10次

最优适应度截图

📊最大权重0.6 最小权重0.1 加速因子 C1:1.3 C2:1.4 种群规模：200，进化次数：1000，实验次数：10次

最优适应度截图


结论：经过研究，在粒子算法初期，选择较大的惯性权重值，可以使得算法有很强得全局搜索能力，而在粒子算法后期选择较小得权重可以使粒子逐渐收敛到全局最优。较高的w设置促进全局搜索，较低的w设置促进快速的局部搜索。设置惯性权重最大值越小，平均最优适应度越低，实验结果越优。所以本实验设置最大权重0.6，最小权重为0.1

④基于适应度函数维数修改对优化函数的影响

📊适应度维度：10 种群规模：200，进化次数：1000，实验次数：10次

📊适应度维度：15 种群规模：200，进化次数：1000，实验次数：10次

📊适应度维度：5 种群规模：200，进化次数：1000，实验次数：10次

结论：维度越低，越容易得到最优解，当维度=5的时候，每次都能找到最优解。维度很高的话，如果种群数量不够多的话，将很难找到最优解。

4.算法总结

• 加速因子c1,c2具有自我总结和向优秀个体学习的能力，从而使微粒向群体内最优点靠近。c1，c2分别调节微粒向个体最优或者群体最优方向飞行的最大步长，决定微粒个体经验和群体经验对微粒自身运行轨迹的影响。学习因子较小时，可能使微粒不在最优区域移动，无法得到最优解；学习因子较大时，可使微粒迅速向最优区域移动，过早收敛。
• 群里规模不能太大，太大反而不太容易找到全局最优解。太小无法体现算法得智能性能
• 维度过小导致算法陷入局部最优，过大增加运行时间，降低效率
• 惯性权重系数，决定了上次迭代速度保留得多少是算法的重要参数之一。算法通过调节它的大小来平衡算法的全局搜索和局部搜索能力。惯性权重采用先行递减的方式进行更新，一般认为，设置较大的，会使得粒子过多的在局部范围内徘徊，不利于全局搜索。设置较小的则会使得粒子过早的陷入局部极值，降低解的精度。