FMCW雷达模块5：角度估计

到达角（AoA）估算的基础

• IF信号的相对物体距离的微小变化非常敏感，具体而言，物体距离的微小变化Δd会导致相位变化ω，其值为4𝜋Δd除以𝜆。角度估计也用了类似的概念。

  

• 角度估算需要至少两个RX天线。利用的是物体相对每个天线的差分距离，TX天线发射一个线性调频脉冲信号，一束射线从物体到达第一个RX天线，另一束设线从物体到达第二个RX天线，而到达第二个RX天线的射线传播稍远一点的距离，即额外的距离Δd，才能到达那里。这个额外的距离Δd会导致额外的相位ω它等于2𝜋Δd除以𝜆。

  

如何使用2个RX天线测量一个物体的AoA

• 下图说明了额外距离与到达角的关系，如果与两个天线之间的距离d相比，物体足够远，从而可以假设从物体到达RX天线的射线是平行的。下图的d是两个天线之间的距离，𝛉是物体相对于雷达的达到角度，设线必须传播的该额外距离结果为dsin𝛉

• TX天线发射一个线性调频脉冲帧，每个RX天线会接收该数据，每个RX天线会处理该数据，并创建一个2D-FFT矩阵，其中包含与物体的距离和速度相对应的峰值，如下图所示，是与该接收器相对应的2D-FFT峰值，以及与该接收器相对应的另一个2D-FFT矩阵，峰值的位置将几乎与这两个2D-FFT相同，这两个峰值的相位差将为2𝜋dsin𝛉，dsin𝛉是额外的距离，然后除以𝜆。通过比较这两个到达信号峰值处的信号来测量的相位差之后，可以求该公式的反函数，并计算到达角。

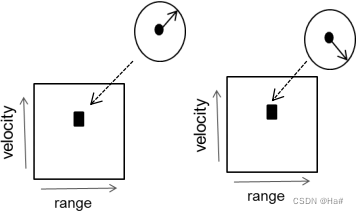
以上求出的𝛉，与测量出的相位差之间的关系是非线性的。在θ =0时，ω对θ的变化最为敏感。ω对𝛉的敏感性随着θ的增加而降低（在θ=90度时变成0），因此，随着θ值的增加，对θ值的估计更容易出错。

角视场，视角范围

• 雷达左侧=> ω>0

• 雷达右侧=> ω<0

• 只要沿顺时针或逆时针方向方向的移动小于180度或pi弧度，对该移动的测量就是明确的

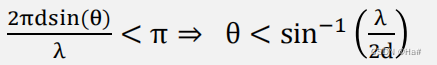
• 间隔为d的两个RX天线可提供服务的最大视场为（间距d为λ/2会导致视野最大）

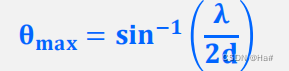
在相同的范围和速度下测量多个物体的AoA

• 假如雷达前方的两个物体，它们相对于雷达有相同的距离和速度，这样这两个物体将处于2D-FFT中相同的距离速度单元，峰值处的值具有来自这两个对象的相量分量。前面所使用的简单相位比较技术不再适用。

• 解决方法：将RX天线的数量从两个增加到N个，并创建N个接收天线的区域，所有这些天线处的二维FFT将在同一个位置具有一个峰值，该系列峰值处的信号将创建一个包含两个旋转相位的离散序列，该序列上的FFT将显示为𝝎1和𝝎2处的两个峰值，其中𝝎1和𝝎2是两个物体的旋转速度，以每个样本的弧度数为单位，就可以通过FFT读取这两个峰值的出现位置，然后计算两个物体的到达角。