IOI2020集训队作业-24,25,26,27,28

24.2 AGC035F Two Histograms

考虑如何建立从可能得到的矩阵到$((l_1,l_2\cdots l_m),(k_1,k_2,\cdots k_n))$的映射。

如果确定了$(k_1,k_2,\cdots k_n)$，显然$(l_1,l_2,\cdots l_m)$也会唯一确定，所以下面只考虑确定$(k_1,k_2\cdots k_n)$。

考虑最后一行，它一定是形如：（一段由1和2组成序列），2，（若干个【可能是0个】1形成的一段），0，（0和1组成的序列）。$k_n$可以取到那一段1中的任何一个位置和那一段1之前的2的位置。我们规定让$k_n$取到那个2的位置。接下来考虑第$n-1$行，情况是类似的，我们也可以做出类似的规定。这样就建立起了一个映射。

而要求一组$(l,k)$可以由一个矩阵通过这个映射得到，等价于要求不存在满足$k_i=j,l_j+1=i$的$(i,j)$。用容斥原理对合法的$(l,k)$计数，得到的就是可能的不同的矩阵的数量。

---

25.2 CF671E Organizing a Race

为了避免混淆，下文用$lim$表示原题中的$k$。

如何判断$[l,r]$是否合法：从$l$开始往$r$走，当汽油不够的时候就给当前城市加汽油使得恰好够走到下一个城市（也就是贪心地使加汽油的城市的位置尽量靠后）；然后把剩下的汽油都加在$r$，从$r$往$l$走判断是否能够走到$l$。

设$pr{e}_i=pr{e}_{i-1}+g_{i-1}-w_{i-1},su{f}_i=su{f}_{i-1}+g_i-w_{i-1}$。则$i$往右第一个无法到达的城市$x$，就是第一个满足$pr{e}_x-pr{e}_i<0$的$x$，我们记为$nex{t}_i=x$，若$x$不存在就记$nex{t}_i=n+1$。而且由于我们在$x-1$加的油量是让我们“恰好可以走到$x$”，所以从$i$到达$x$之后，再次出发时得到的油量就是$g_x$，所以下一个走不到的点就是$nex{t}_x$。将$nex{t}_i$作为$i$的父亲，会得到一个树形结构，并且{n+1,n,n−1,n−2⋯1}\{n+1,n,n-1,n-2\cdots 1\}{n+1,n,n−1,n−2⋯1}是这棵树的一个dfs序。

对整棵树进行dfs，令当前走到的点为$l$（也等价于从右到左枚举$l$），并对每个点维护$g_i^{\prime }$表示如果从$l$出发要走到$i+1$需要在这个城市额外加的油量（根据第一段描述的贪心策略），以及相应的$su{f}_i^{\prime },cos{t}_i$，其中$cos{t}_i={\sum }_{l\le k\le i}{g}_k^{\prime }-g_k$。从$nex{t}_i$走到$i$，会对$g_k^{\prime },su{f}_k^{\prime },cos{t}_k$造成的影响是：

• $g_{nex{t}_i-1}^{\prime }+=pre[i]-pre[nex{t}_i]$
• $su{f}_k^{\prime }+=pre[i]-pre[nex{t}_i](\forall k\ge nex{t}_i-1)$
• $cos{t}_k+=pre[i]-pre[nex{t}_i](\forall k\ge nex{t}_i-1)$

一个$r$合法的充要条件就是(costr−(gr′−gr))−min⁡l≤k<r{(sufr′−(gr′−gr))−sufk′}≤lim(cost_r-(g'_r-g_r)) - \min_{l\le k<r} \{(suf'_r-(g'_r-g_r))-suf'_k\} \le lim(costr​−(gr′​−gr​))−minl≤k<r​{(sufr′​−(gr′​−gr​))−sufk′​}≤lim且$cos{t}_r\le lim$，其中减去$g_r^{\prime }-g_r$是因为我们并不需要到达$r+1$。上面的表达式等价于max⁡l≤k<r{sufk′}+costr−sufr′≤lim∧costr≤lim\max_{l\le k<r}\{suf'_k\} + cost_r - suf'_r\le lim\wedge cost_r\le limmaxl≤k<r​{sufk′​}+costr​−sufr′​≤lim∧costr​≤lim。

由于每一次对$su{f}_r^{\prime },cos{t}_r$的修改量是相同的，所以$cos{t}_r-su{f}_r^{\prime }$对于每一个$r$都是一个定值，我们只需要维护对$su{f}^{\prime }$的修改。在线段树上对$r$二分，只要支持快速查询一个区间内的min⁡{max⁡l≤k<r{sufk′}+costr−sufr′}\min \{\max_{l\le k<r}\{suf'_k\} + cost_r - suf'_r\}min{maxl≤k<r​{sufk′​}+costr​−sufr′​}就能够判定一个区间内是否存在合法的$r$，这个用bzoj2957那道题的套路就可以维护。注意不能选择$cos{t}_r>lim$的那些$r$，由于那些$r$形成的是一段后缀，可以二分找出那段后缀的长度，然后对那段后缀的点的$su{f}^{\prime }$都加上$\infty$。

总时间复杂度$O(n{\log }^{2}n)$。

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define PB push_back
#define MP make_pair
#define PII pair<int,int>
#define FIR first
#define SEC second
#define ll long long
using namespace std;
template <class T>
inline void rd(T &x) {
	x=0; char c=getchar(); int f=1;
	while(!isdigit(c)) { if(c=='-') f=-1; c=getchar(); }
	while(isdigit(c)) x=x*10-'0'+c,c=getchar(); x*=f;
}
#define ls (c<<1)
#define rs (c<<1|1)
const int N=1e5+10,M=N*4;
const ll inf=1e16;
ll sum[M],mx[M],mi[M],tg[M];
inline void add(int c,ll t) { tg[c]+=t,sum[c]+=t,mx[c]+=t; }
inline void push_down(int c) { if(tg[c]) add(ls,tg[c]),add(rs,tg[c]),tg[c]=0; }
ll query(int l,int r,int c,ll v) {
    if(l==r) return v+mi[c];
    int mid=l+r>>1; push_down(c);
    if(v<=mx[ls]) return min(query(l,mid,ls,v),sum[c]);
    return min(v+mi[ls],query(mid+1,r,rs,v));
}
void push_up(int c,int l,int r) {
    mx[c]=max(mx[ls],mx[rs]);
    int mid=l+r>>1; sum[c]=query(mid+1,r,rs,mx[ls]);
}
ll suf[N],pre[N];
void build(int l,int r,int c) {
    if(l==r) return (void)(mi[c]=-suf[l],mx[c]=suf[l],sum[c]=inf);
    int mid=l+r>>1;
    build(l,mid,ls),build(mid+1,r,rs);
    mi[c]=min(mi[ls],mi[rs]); push_up(c,l,r);
}
int ql,qr; ll qt;
void upd(int l,int r,int c) {
    if(ql<=l&&qr>=r) return add(c,qt);
    int mid=l+r>>1; push_down(c);
    if(ql<=mid) upd(l,mid,ls);
    if(qr>mid) upd(mid+1,r,rs);
    push_up(c,l,r);
}
int m,n,g[N],w[N];
int Q(int l,int r,int c,ll d) {
    if(query(l,r,c,d)>m) return 0;
    if(l==r) return l;
    int mid=l+r>>1,t=0; push_down(c);
    if(t=Q(mid+1,r,rs,max(d,mx[ls]))) return t;
    return Q(l,mid,ls,d);
}
void ins(int x,int f,int d) {
    if(f<=n) {
        ql=f-1,qr=n,qt=d*(pre[x]-pre[f]);
        upd(1,n,1);
    }
}
int st[N],top;
int main() {
    rd(n),rd(m);
    for(int i=1;i<n;++i) rd(w[i]);
    for(int i=1;i<=n;++i) rd(g[i]);
    for(int i=1;i<=n;++i) {
        pre[i]=pre[i-1]+g[i-1]-w[i-1];
        suf[i]=suf[i-1]+g[i]-w[i-1];
    }
    build(1,n,1);
    st[0]=n+1; int ans=0;
    for(int i=n;i>=1;--i) {
        while(top&&pre[st[top]]>=pre[i]) ins(st[top],st[top-1],-1),top--;
        ins(i,st[top],1); st[++top]=i;
        int lb=0,rb=top;
        while(lb<rb) {
            int mid=lb+rb>>1;
            if(pre[i]-pre[st[mid]]<=m) rb=mid;
            else lb=mid+1;
        }
        if(i>1) { ql=1,qr=i-1,qt=-inf; upd(1,n,1); }
        if(rb>1) { ql=st[rb-1]-1,qr=n,qt=inf; upd(1,n,1); }
        ans=max(ans,Q(1,n,1,-inf)-i+1);
        if(i>1) { ql=1,qr=i-1,qt=inf; upd(1,n,1); }
        if(rb>1) { ql=st[rb-1]-1,qr=n,qt=-inf; upd(1,n,1); }
        // cout<<i<<':'<<ans<<endl;
    }
    printf("%d",ans);
    return 0;
}

---

26.3 ARC095F Permutation Tree

我们令$q_i$表示$i$这个元素在$p$中出现的位置。则建树的过程等价于是：对于每一个$i>1$，在$q_i$和max⁡j<i{qj}\max_{j<i}\{q_j\}maxj<i​{qj​}之间连一条边。

则得到的树的形态一定会有如下的形式：

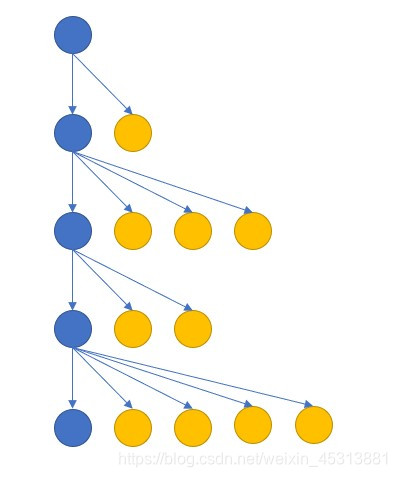
其中蓝色的点是满足$\forall j<i,q_j<q_i$的那些$q_i$。

找出树的直径，则每个点要么在直径上，要么与直径相邻，否则一定无解。

假设现在我们确定了树的层次结构（确定了哪个点是根，以及每个点的颜色），要确定一个最优的排列$p$，策略应该是这样的：第$i$层的蓝色点的$q_i$是（它前面的层的点数 + 这一层的点数），而第$i$层的那些黄色点的$q_i$从（前面的层的点数 + 1）开始，依次递增取。以上面的图为例，我们得到的$q$是这样的：1,3,2,7,4,5,6,10,8,9,15,11,12,13,14。

尽管对于一个具体的排列$q$，我们建出来的树中，最后一个蓝色点可能是有儿子的；但是现在我们只知道树的形态，如果我们构造出来的最后一个蓝色点有儿子的话，让那个儿子成为蓝色点显然会得到更优的答案。所以第一个蓝色点和最后一个蓝色点分别是直径的两端。枚举哪一个是根，然后在两个答案中取一个更优的就可以了。

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define PB push_back
#define MP make_pair
#define FIR first
#define SEC second
#define ll long long
using namespace std;
template <class T>
inline void rd(T &x) {
	x=0; char c=getchar(); int f=1;
	while(!isdigit(c)) { if(c=='-') f=-1; c=getchar(); }
	while(isdigit(c)) x=x*10-'0'+c,c=getchar(); x*=f;
}
const int N=1e5+10;
int n;
vector<int> G[N];
int mxd,cur;
void dfs1(int u,int last,int d) {
	if(d>mxd) mxd=d,cur=u;
	for(int i=0;i<G[u].size();++i)
		if(G[u][i]!=last) dfs1(G[u][i],u,d+1);
}
int st[N],top;
int mk[N];
vector<int> L;
void dfs2(int u,int last,int T) {
	st[++top]=u;
	if(u==T) {
		for(int i=1;i<=top;++i) mk[st[i]]=1,L.PB(st[i]);
	}
	for(int i=0;i<G[u].size();++i)
		if(G[u][i]!=last) dfs2(G[u][i],u,T);
	top--;
}
void sol(int *P) {
	int m=0;
	P[++m]=1;
	for(int i=1;i+1<L.size();++i) {
		int l=m+1,r=m+G[L[i]].size()-1;
		P[++m]=r;
		for(int j=l;j<r;++j) P[++m]=j;
	}
	P[++m]=n;
}
int P[N],Q[N];
int main() {
	rd(n);
	for(int i=1,x,y;i<n;++i) rd(x),rd(y),G[x].PB(y),G[y].PB(x);
	mxd=-1; dfs1(1,0,0); int L1=cur;
	mxd=-1; dfs1(cur,0,0); int L2=cur;
	dfs2(L1,0,L2);
	for(int i=1;i<=n;++i) {
		int flg=mk[i];
		for(int j=0;!flg&&j<G[i].size();++j)
			flg|=mk[G[i][j]];
		if(!flg) {
			printf("-1");
			return 0;
		}
	}
	sol(P);
	reverse(L.begin(),L.end());
	sol(Q);
	for(int i=1;i<=n;++i)
		if(P[i]!=Q[i]) {
			if(P[i]>Q[i]) swap(P,Q);
			break;
		}
	for(int i=1;i<=n;++i) Q[P[i]]=i;
	for(int i=1;i<=n;++i) printf("%d ",Q[i]);
	return 0;
}

---

28.1 CF585E Present for Vitalik the Philatelist

答案等价于（用$\gcd (S)$表示$S$集合中的数的$\gcd$）：

$$\begin{gathered} \sum _S|S|\cdot [\gcd (S)=1]-\sum _S(n-|S|)\cdot [\gcd (S)=1] \\ =2\cdot \sum _S|S|\cdot [\gcd (S)=1]-n\sum _S[\gcd (S)=1] \end{gathered}$$

令$A_d$表示${\sum }_i[d\mid a_i]$，$A$可以在O(max⁡{ai})O(\max\{a_i\})O(max{ai​})的时间通过高维前缀和求出。

对${\sum }_S[\gcd (S)=1]$直接莫比乌斯反演得到${\sum }_d(2^{A_d}-1)\mu (d)$。

而${\sum }_S|S|\cdot [\gcd (S)=1]$等价于${\sum }_i{\sum }_{a_i\in S}[\gcd (S)=1]$，反演得到${\sum }_d\mu (d)\cdot 2^{A_d-1}\cdot A_d$。

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define PB push_back
#define MP make_pair
#define PII pair<int,int>
#define FIR first
#define SEC second
#define ll long long
using namespace std;
template <class T>
inline void rd(T &x) {
	x=0; char c=getchar(); int f=1;
	while(!isdigit(c)) { if(c=='-') f=-1; c=getchar(); }
	while(isdigit(c)) x=x*10-'0'+c,c=getchar(); x*=f;
}
const int M=1e7+10,N=5e5+10;
const int mod=1e9+7;
int pri[M],mu[M],num;
void getpri(int n) {
    static int d[M];
    mu[1]=1;
    for(int i=2;i<=n;++i) {
        if(!d[i]) pri[d[i]=++num]=i,mu[i]=-1;
        for(int j=1;j<=d[i]&&pri[j]*i<=n;++j) {
            d[i*pri[j]]=j;
            if(j!=d[i]) mu[i*pri[j]]=-mu[i];
        }
    }
}
int n,a[N],d[M],m;
int pw[N];
int main() {
    getpri(m=10000000);
    rd(n);
    for(int i=1;i<=n;++i) rd(a[i]),d[a[i]]++;
    for(int j=1;j<=num;++j)
        for(int i=m/pri[j]*pri[j];i;i-=pri[j]) if(d[i])
            d[i/pri[j]]+=d[i];
    pw[0]=1; for(int i=1;i<=n;++i) pw[i]=pw[i-1]*2ll%mod;
    int ans1=0,ans2=0;
    for(int i=1;i<=m;++i) if(d[i]) {
        if(mu[i]) ans2=(ans2+mu[i]*(pw[d[i]]-1))%mod;
        ans1=(ans1+mu[i]*pw[d[i]-1]*(ll)d[i])%mod;
    }
    int ans=(ans1*2ll-ans2*(ll)n)%mod;
    printf("%d",(ans+mod)%mod);
    return 0;
}

---

28.2 AGC032C Three Circuits

如果存在度数为奇数的点显
然是No。

如果有点的度数大于等于$6$，说明这张图的欧拉回路会经过这个点至少三次，可以直接通过把欧拉回路拆成环来构造，所以答案是Yes。

接下来考虑所有点的度数都是$4$或者$2$的情况。

如果有至少三个点的度数为$4$，答案是Yes。用$A,B,C$分别表示三个点，找出一条欧拉回路，将回路从每一次经过$A$的地方断开得到两个不相交的环。如果$B$或者$C$在同一个环上出现过两次，就可以把那个环从$B$或者$C$两次出现的位置断开得到两个环；否则，每个环上$B,C$恰好出现了一次，所以$B,C$之间，$A,B$之间，$C,A$之间都存在两条边不相交的路径，可以构造$A\to B\to A,B\to C\to B,C\to A\to C$这三个环。

如果只有两个点度数为$4$，我们首先把度为$2$的点缩成一条边，那么就只有这样两种情况：

• 边集为：$(1,2),(1,2),(1,1),(2,2)$，答案是Yes，构造$(1,2),(2,1)$和$(1,1)$和$(2,2)$即可得到三个环。
• 边集为：$(1,2),(1,2),(1,2),(1,2)$，此时答案是No。

若度数为$4$的点数小于$2$，答案显然是No。

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define FAIL {printf("No");exit(0);}
#define SUCC {printf("Yes");exit(0);}
#define PB push_back
#define MP make_pair
#define PII pair<int,int>
#define FIR first
#define SEC second
#define ll long long
using namespace std;
template <class T>
inline void rd(T &x) {
	x=0; char c=getchar(); int f=1;
	while(!isdigit(c)) { if(c=='-') f=-1; c=getchar(); }
	while(isdigit(c)) x=x*10-'0'+c,c=getchar(); x*=f;
}
const int N=1e5+10;
vector<int> G[N],S;
int n,m,vis[N];
int dfs(int u,int last) {
    if(vis[u]) return vis[u];
    for(int i=0;i<G[u].size();++i)
        if(G[u][i]!=last) return vis[u]=dfs(G[u][i],u);
}

int main() {
    rd(n),rd(m);
    for(int i=1;i<=m;++i) {
        int x,y; rd(x),rd(y);
        G[x].PB(y),G[y].PB(x);
    }
    for(int i=1;i<=n;++i) if(G[i].size()&1) FAIL;
    for(int i=1;i<=n;++i) if(G[i].size()>=6) SUCC;
    for(int i=1;i<=n;++i) if(G[i].size()==4) S.PB(i);
    if(S.size()>=3) SUCC;
    if(S.size()<2) FAIL;
    int s=S[0],t=S[1];
    vis[s]=1,vis[t]=2;
    for(int i=1;i<=n;++i) if(!vis[i]) {
        if(dfs(G[i][0],i)==dfs(G[i][1],i)) SUCC;
        vis[i]=3;
    }
    FAIL;
}