机器学习—交叉熵代价函数—极大似然估计推导

最新推荐文章于 2025-07-05 10:11:49 发布
原创 最新推荐文章于 2025-07-05 10:11:49 发布 · 2.4k 阅读 · 4 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#极大似然估计 #交叉熵代价函数 #逻辑回归代价函数

本文深入探讨了逻辑回归模型及其背后的数学原理，通过极大似然估计推导出了交叉熵代价函数，揭示了逻辑回归如何通过Sigmoid函数预测样本属于正例的概率，并通过最大似然估计构建了逻辑回归的代价函数。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

一、极大似然估计

首先得知道什么是极大似然估计

吴恩达老师在公开课直接给出交叉熵代价函数并简单解释了交叉熵代价函数作为逻辑回归代价函数的合理性，在周志华老师的《机器学习》教材中，从极大似然估计角度详细证明了交叉熵代价函数的推导。

二、逻辑回归模型

周志华老师从模型开始详细的介绍了逻辑回归的由来与其实质。
在这里插入图片描述
加入Sigmoid函数后得出
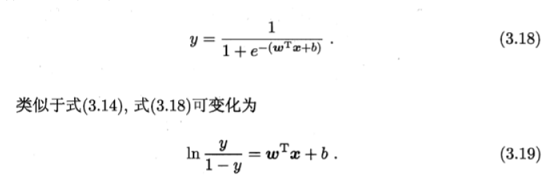
在这里插入图片描述
而在经过进一步的计算y=0和y=1时的概率
在这里插入图片描述
最终某样本属于正例的概率可以表示为
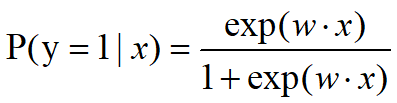
在这里插入图片描述
某样本属于负例的概率可以表示为
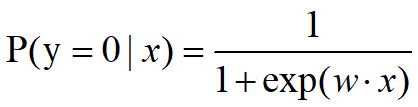
在这里插入图片描述
将w·x视为Sigmoid函数的输入，其中w是模型参数，x是特征向量，将Sigmoid函数的输出视为预测为正例的概率。

那模型将样本预测为正例的概率为sigmod(w·x)；将样本预测为负例概率为1- sigmod(w·x)。

三、极大化目标

极大化 => 将所有正例预测为正例的概率的累乘 * 将所有负例预测为负例的概率的累乘
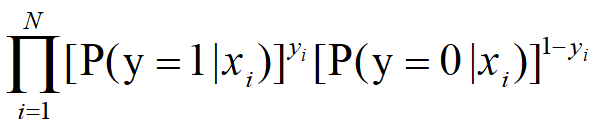
在这里插入图片描述
而在计算机中通常求最小化问题，对上述公式运用对数法则对数似然并转换为求解最小化问题得出交叉熵代价函数：
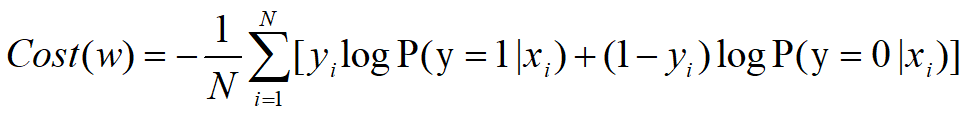
在这里插入图片描述

四、使用极大似然估计构建逻辑回归代价函数另一种写法

在这里插入图片描述

五、最大似然估计和最小代价函数两种方式推导逻辑回归

大佬链接：
最大似然估计和最小代价函数两种方式推导逻辑回归

交叉熵函数推导
ZJF的博客
05-12 890
交叉熵的推导 1.最大似然 何为最大似然？哲学上有句话叫做“存在就是合理的”，最大似然的意思是“存在就是最合理的”。具体来说，如果事件XXX的概率分布为p(X)p(X)p(X)，如果一次观测中具体观测到的值分别为X1,X2,…,XnX_1,X_2,…,X_nX1​,X2​,…,Xn​，并假设它们是相互独立，那么 P=∏i=1np(Xi)(1) \mathcal P=\prod_{i=1}^np(X_i) \tag{1} P=i=1∏n​p(Xi​)(1) 是最大的。如果p(X)p(X)p(X)是一个带有参数
交叉熵代价函数（作用及公式推导）
热门推荐
Arthur-Chen的专栏
04-02 12万+
交叉熵代价函数（Cross-entropy cost function）是用来衡量人工神经网络（ANN）的输出值与实际值的一种方式。与二次代价函数（Quadratic cost function）相比，它能更有效地配合反向传播算法，促进ANN的训练。
交叉熵的理解
最新发布
abc2812365481的博客
07-05 330
交叉熵衡量的是两个概率分布之间的“距离”；在机器学习中，是分类任务的标准损失函数；强调惩罚低置信预测，即当模型对真实类别的预测概率趋近于 0 时，损失趋近于。%24c%24。
理解交叉熵和最大似然估计的关系
elite666的专栏
11-08 8496
理解交叉熵作为神经网络的损失函数的意义： 交叉熵刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近，即拟合的更好。 cross entropy= H§+DKL(p||q) 当p分布是已知，则熵是常量；于是交叉熵和KL散度则是等价的。 最小化KL散度和模型采用最大似然估计进行参数估计又是一致的。（可以从公式推导上证明） 这也是很多模型又采用最大似然估计作为损...
最大化似然估计，交叉熵
weixin_42668508的博客
12-13 493
最大似然估计，交叉熵
【机器学习】交叉熵的推导
LogM的博客
07-02 1260
极大似然推导交叉熵，信息熵角度解释交叉熵
最大似然估计与损失函数
jediael_lu的专栏
07-14 7543
关于最大似然估计法的基本原理请参考《概率论与数理统计》P152或参考《深度学习》chpt 5.5 文章目录1、最大似然估计的一般理论2、最大似然估计的性质3、最大似然估计推导逻辑回归的损失函数4、线性回归的损失函数5、小结 1、最大似然估计的一般理论 我们希望可以有些准则可以让我们从不同的模型中得到特定函数作为好的估计。 最常用的准则是最大似然估计。 我们考虑一组含有m个样本的数据集X={x(1),...,x(m)}X=\{x^{(1)},...,x^{(m)}\}X={x(1),...,x(m)}，独立的
DeepLearning学习笔记——极大似然估计
hustqb的博客
08-14 6017
简介 条件对数似然和均方误差 最大似然的性质一般提到估计，我们首先想到的是通过输入，估计输出。这时，有很多准则，比如偏差和方差来帮我们估计。然而有时候，我们希望有些方法可以让我们估计输入到输出的函数（当函数模型确定时，就是估计函数的参数）。这些函数由于模型和参数的不同而不同，它们组成了在机器学习中常说的函数空间。极大似然估计就可以帮我们从函数空间中选定特定的函数作为好的估计简单来说，就对于y=f(x
【机器学习入门】交叉熵损失函数与MLE准则
jasonso97的博客
01-17 1609
交叉熵损失函数最小化与MLE估计是等价的，不同的任务（如线性回归、二分类、多分类）导出的交叉熵损失函数具体样子不同。这篇文章对以上三种任务的交叉熵损失函数\代价函数进行了一定的推导介绍。
交叉熵损失函数优缺点_【损失函数】常见的损失函数(loss function)总结
weixin_39520595的博客
12-19 5939
阅读大概需要7分钟跟随小博主，每天进步一丢丢机器学习算法与自然语言处理出品@公众号原创专栏作者yyHaker单位 |哈工大SCIR实验室损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越好，通常模型的性能越好。不同的模型用的损失函数一般也不一样。损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是指经验风险损失函数加上正则项。...
损失函数与代价函数
qq_44159782的博客
10-16 2569
【版权申明】未经博主同意，谢绝转载！（请尊重原创，博主保留追究权）； 本博客的内容来自于：java常见面试考点（四十三）：泛型； 学习、合作与交流联系q384660495； 本博客的内容仅供学习与参考，并非营利； 文章目录一、 损失函数、代价函数与目标函数二、常见的损失函数常见的代价函数 一、 损失函数、代价函数与目标函数 损失函数（Loss Function）：是定义在单个样本上的，是指一个样本的误差。 代价函数（Cost Function）：是定义在整个训练集上的，是所有样本误差的平均，也就是所..
softmax的交叉熵导数推导.docx
05-16
本文为softmax 的交叉熵 求导公式，来源于斯坦福cs224n 其中一题
最大似然估计与交叉熵
muyuu的博客
11-30 2021
熵，交叉熵，相对熵，最大似然估计，最大熵熵交叉熵相对熵（KL散度）最大似然估计最大熵 熵 熵是信息论中的概念，首先需要定义一个事件X=xX=xX=x的信息量，要求满足以下两个条件： 越不可能发生的事情，信息越大 几个独立事件同时发生的信息量=每一个事件的信息量之和 个满足以上两个条件的且最为简单的函数就是对数函数了，s.t. I(x)=−logP(x)I(x) = -logP(x)I(x)=−logP(x) Proof： 1. P(x)P(x)P(x)越大，I(x)=−logP(x)I(x) = -log
交叉熵与极大似然:
独钓寒江雪
08-26 883
KL散度、交叉熵与极大似然: https://www.cnblogs.com/jenny1000000/p/7745458.html KL散度、交叉熵与极大似然: http://www.360doc.com/content/17/1105/09/31747150_701004922.shtml  
极大似然估计与交叉熵
qq_34372112的博客
09-09 3327
前言 关于极大似然估计和交叉熵我就不介绍了，有兴趣的可以看我其他的博客，我这里只讲他们的联系。 公式 现有一个真实的分布 P(x)P(x)P(x)，现在为了减小模型的概率分布 Q(x;θ)Q(x;\theta)Q(x;θ) 与真实分布P之间的差异，使用最大似然： θMLE=argmax⁡∏i=1mQ(xi;θ)=argmax⁡∑i=1mlog⁡Q(xi;θ)≈argmax⁡Ex∼P(x)[log⁡...
【机器学习】分别从极大似然和熵的角度来看交叉熵损失
Mr_health的博客
07-28 539
从极大似然的角度 从熵的角度 假设样本为X，其对应的类别为Y，P(Y|X)就是给定X判断为Y的后验概率。我们希望每一个样本X被正确预测到相应类别Y的概率都最大，即max P(Y|X)，那么所有样本正确预测概率相乘最大化就是我们所期望的，因此采用极大似然的原理 Step1：构...
线性回归--经验最小化，结构最小化，最大似然估计，最大后验估计
baochunlei1的博客
12-08 1197
自己开发了一个股票智能分析软件，功能很强大，需要的点击下面的链接获取： https://www.cnblogs.com/bclshuai/p/11380657.html 1.1 线性回归 1.1.1 原理简介 线性回归是对一次函数的拟合y=θ1x1+……+θixi+b，其中xi为自变量，每一个输入向量（x1……xi）就是一个特征向量，可以用最小二乘法推导出参数矩阵计算公式，也可以用迭代的方法求出参数值。设定损失函数，一般为误差均方根（RMSE），或者直接用均方误差，对参数求偏导数，...
交叉熵函数推导CrossEntropy
专注“目标检测”领域技术分享
10-03 3748
本文演示了如何从零推导出交叉熵函数。通过对于下面这些概念的讲解，信息量、熵、KL散度，作者演示了交叉熵是如何从信息量的概念一步步推导到交叉熵。下一步作者对于交叉熵函数进行了变形，最后推导出用softmax函数表示交叉熵函数的公式。pytorch内置了这个函数F.log_softmax来实现上面这个公式。
机器学习中的代价函数
06-30
交叉熵代价函数的优势在于它能够直接反映预测概率与真实标签之间的差异，并且在反向传播过程中提供了更稳定的梯度更新方向 [^3]。 --- ### 代价函数的公式推导 以逻辑回归中的代价函数为例，其目标是最大化似然...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值