支持向量机（SVM）

一、优化目标

1.1 支持向量机

支持向量机（Support Vector Machine），简称SVM，在学习复杂的非线性方程时提供了一种更为清晰强大的方式。

用z表示θ^Tx
如果有一个y=1的样本，则希望h（x）≈ 1，θ^Tx >> 0；
如果有一个y=0的样本，则希望h（x）≈ 0，θ^Tx << 0；

1.2 建立支持向量机

当y=1时，

y=0时，

建立支持向量机

①无论是否有1/m这一项，最终得到的最优值θ都是一样的
②对于逻辑回归，在目标函数中，有两项：训练样本的代价和正则化项，需要用这一项来平衡。

A+λ×B，通过设置不同正则参数λ达到优化的目的，权衡对应的项，使得训练样本拟合的更好。如果给定的λ具有很大的值，意味着给予B更大的权重

对于支持向量机，C×A+B，如果C设定为非常小的值，那么会给B比A更大的权重

得到在支持向量机中我们的整个优化目标函数，最小化目标函数，得到SVM学习到的参数C

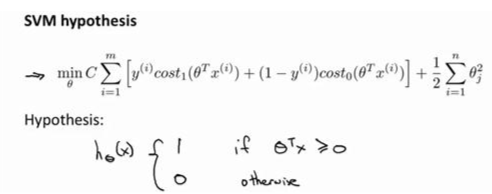
当θ^Tx ≥ 0时，学习参数θ是支持向量机假设函数的形式

二、大边界的直观理解

2.1 代价函数

左图表正样本，y = 1，关于z的代价函数cost₁^(z)，当θ^Tx ≥ 1 时，cost₁^(z) = 0

右图表负样本，y = 0，关于z的代价函数cost₀^(z)，当θ^Tx ≤ -1 时，cost₀^(z) = 0