【剑指 Offer 38. 字符串的排列】_剑指offer jz38 字符串的排列-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_45134475/article/details/123934393

本文介绍如何使用深度优先搜索算法解决字符串排列问题，并针对重复字符进行剪枝，以避免重复排列。讲解了如何在Java中实现字符排列的递归函数，以及复杂度分析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

排列
剪枝
字符串

题目描述

输入一个字符串，打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

示例:

输入：s = “abc”
输出：[“abc”,“acb”,“bac”,“bca”,“cab”,“cba”]

解题思路：
对于一个长度为 nn 的字符串（假设字符互不重复），其排列方案数共有：
$\times (n-1) \times (n-2) … \times 2 \times 1$

排列方案的生成：

根据字符串排列的特点，考虑深度优先搜索所有排列方案。即通过字符交换，先固定第 1 位字符（ n 种情况）、再固定第 2 位字符（ n-1 种情况）、… 、最后固定第 n 位字符（ 1 种情况）。
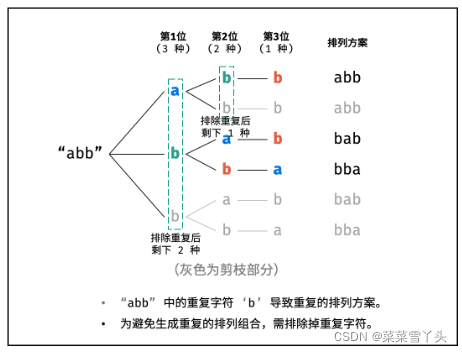
在这里插入图片描述
重复排列方案与剪枝：

当字符串存在重复字符时，排列方案中也存在重复的排列方案。为排除重复方案，需在固定某位字符时，保证 “每种字符只在此位固定一次” ，即遇到重复字符时不交换，直接跳过。从 DFS 角度看，此操作称为 “剪枝” 。
在这里插入图片描述

class Solution {
    List<String> res = new LinkedList<>();
    char[] c;
    public String[] permutation(String s) {
        c = s.toCharArray();
        dfs(0);
        return res.toArray(new String[res.size()]);
    }
    void dfs(int x) {
        if(x == c.length - 1) {
            res.add(String.valueOf(c));      // 添加排列方案
            return;
        }
        HashSet<Character> set = new HashSet<>();
        for(int i = x; i < c.length; i++) {
            if(set.contains(c[i])) continue; // 重复，因此剪枝
            set.add(c[i]);
            swap(i, x);                      // 交换，将 c[i] 固定在第 x 位
            dfs(x + 1);                      // 开启固定第 x + 1 位字符
            swap(i, x);                      // 恢复交换
        }
    }
    void swap(int a, int b) {
        char tmp = c[a];
        c[a] = c[b];
        c[b] = tmp;
    }
}
作者：jyd
链接：https://leetcode-cn.com/problems/zi-fu-chuan-de-pai-lie-lcof/solution/mian-shi-ti-38-zi-fu-chuan-de-pai-lie-hui-su-fa-by/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

复杂度分析

时间复杂度 $O (N! N)$ ： N 为字符串 s 的长度；时间复杂度和字符串排列的方案数成线性关系，方案数为 $\times (N-1) \times (N-2) … \times 2 \times 1$ ，即复杂度为 O(N!) ；字符串拼接操作 join() 使用 O(N) ；因此总体时间复杂度为 O(N!N) 。
空间复杂度 $O(N^2)$ ：全排列的递归深度为 N ，系统累计使用栈空间大小为 O(N) ；递归中辅助 Set 累计存储的字符数量最多为 $N + (N - 1) + . . . + 2 + 1 = (N + 1) N / 2$ ，即占用 $O(N^2)$ 的额外空间。