LeetCode第1天 | 动态规划 | 20220713

LeetCode第1天 | 动态规划 | 20220713

最大子数组和、动态规划、线段树、分治

本文章参考了许多他人的笔记，仅供自己学习复习使用。
leetcode官网
liweiwei李威威：解答多为java编写，思路非常清晰，读他的笔记对学习很有帮助。
负雪明烛：偶然在知乎看到，受到其leetcode刷题建议的指导。5 年在 优快云 上更新了 800多道题解，收获 160万 阅读。在中文力扣日更题解。

---

---

【第一题】 53. 最大子数组和

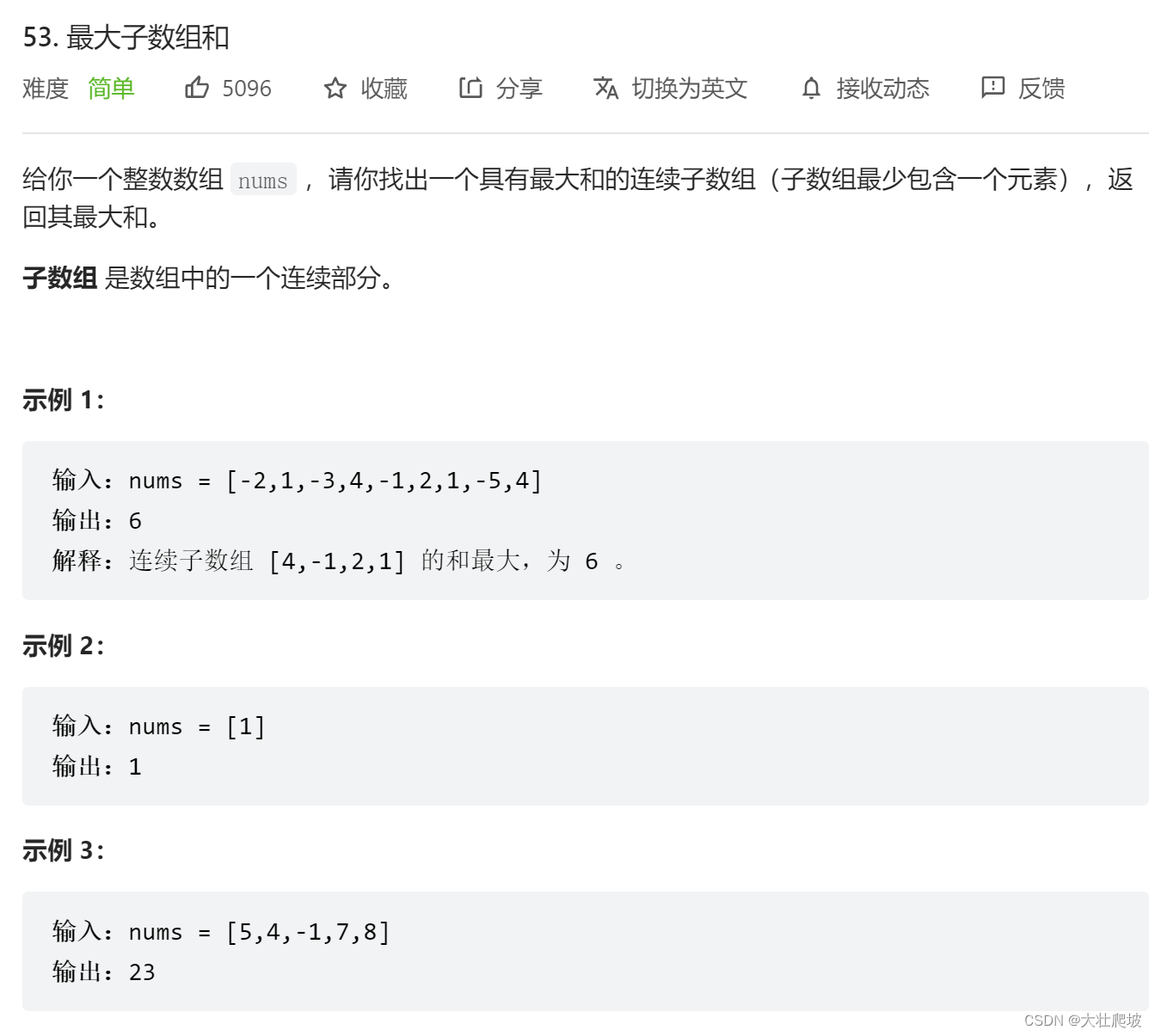
1.1 方法一 动态规划

1.1.1 贪心算法

若当前指针所指元素之前选中的子数列的和小于0，则丢弃当前元素之前选中的子数列（个人觉得这样的表述比官网原先的更符合理解）

1.1.2 代码

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if(nums.size() == 0)
            return -2147483648;
        
        int pre_sum = 0;
        int cur_sum = 0;
        int max_sum = 0;

        for(int i = 0; i<nums.size();i++){
            /*
            cur_sum 当前和
            max_sum 当前最大和
            pre_sum 之前i-1和

            当pre_sum < 0时，max(nums[i], pre_sum + nums[i]) = nums[i],
            相当于抛弃前面所包含的子序列
            */

            cur_sum = max(nums[i], pre_sum + nums[i]);
            max_sum = max(cur_sum, max_sum);
            pre_sum = cur_sum;
            /*代码可以更简洁：
            cur_sum = max(nums[i], cur_sum + nums[i]);
            max_sum = max(cur_sum, max_sum);
            */
        }

        return max_sum;
    }
};

1.1.3 问题与解决

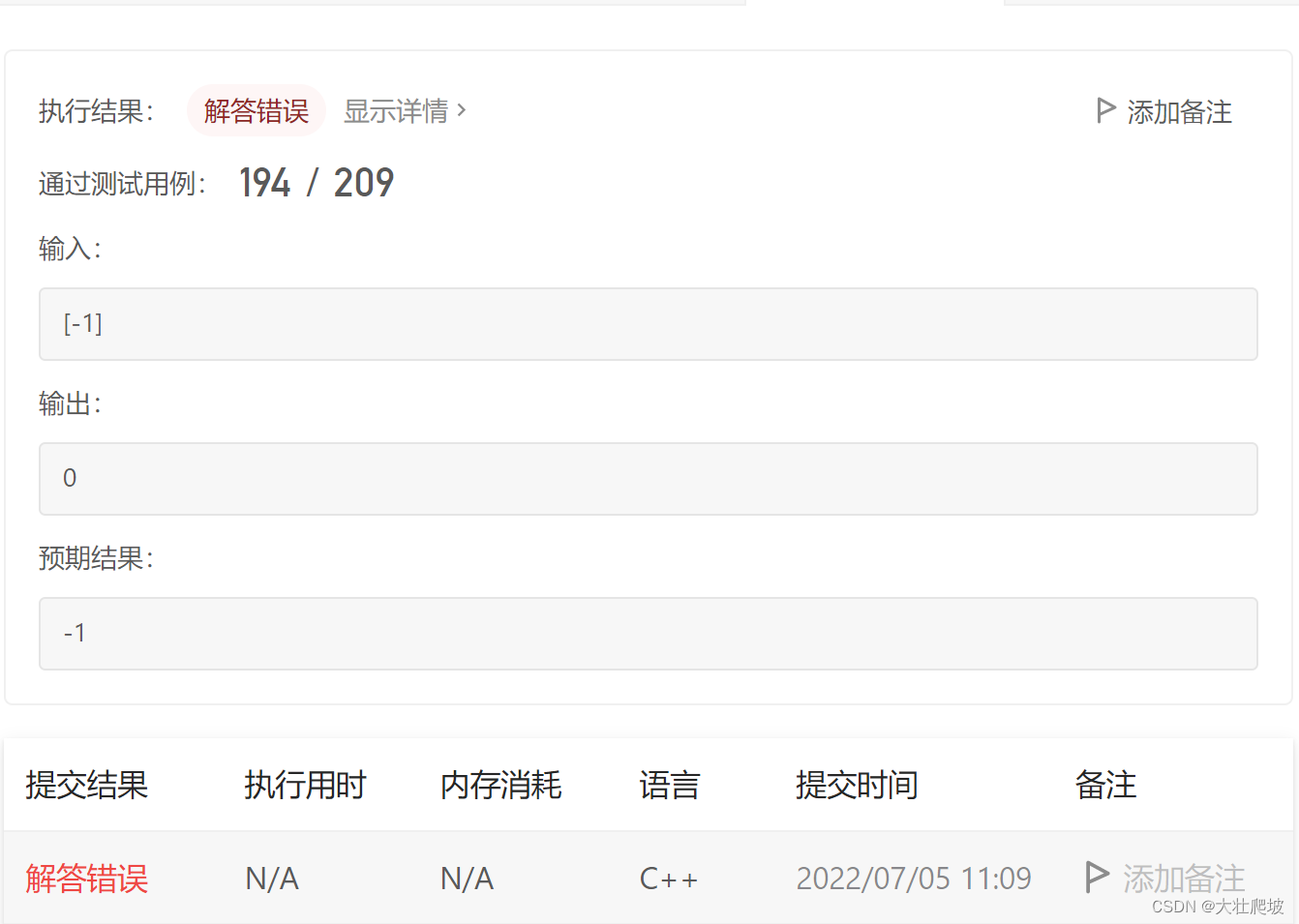
输入-1却输出0，问题出在max_sum设置的初始值。看看自己的代码：

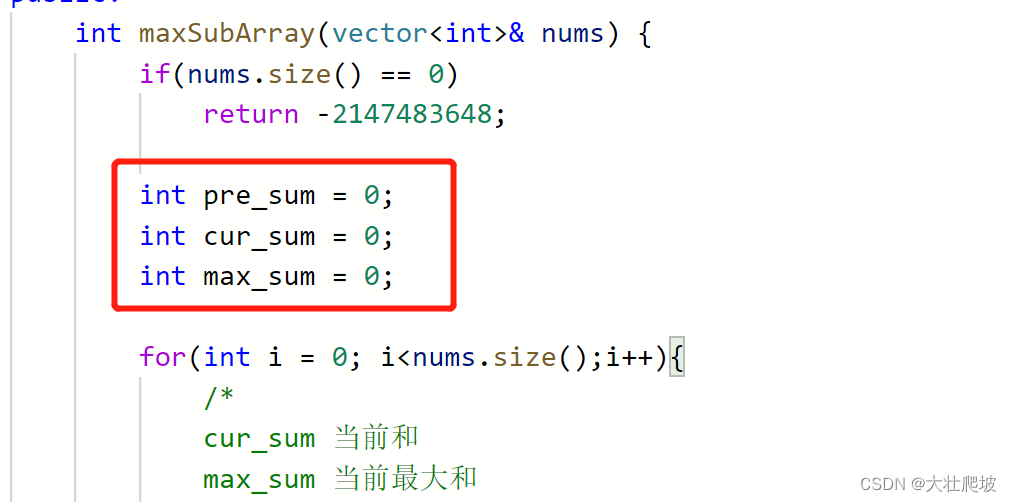
修改后成功通过：

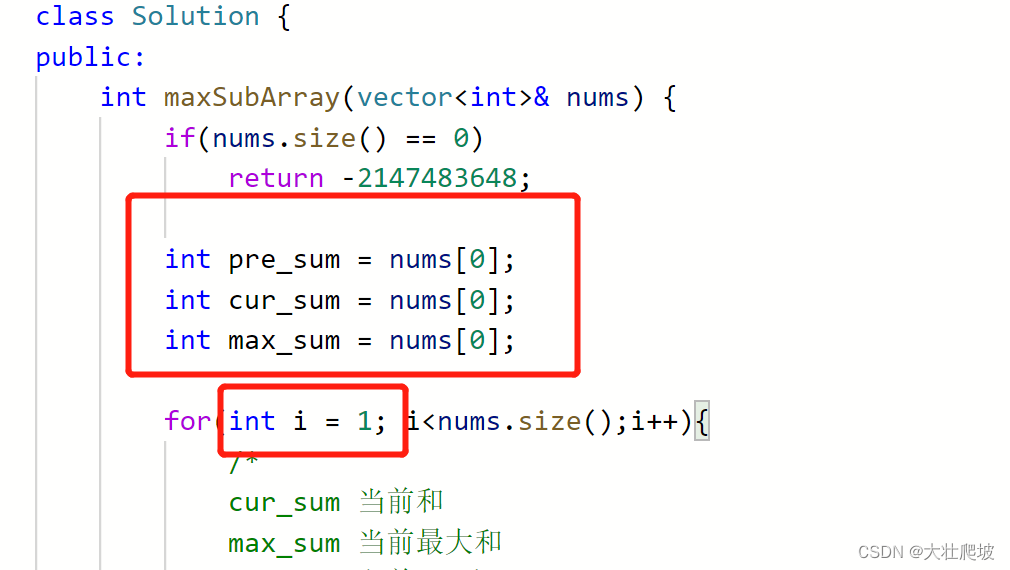
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if(nums.size() == 0)
            return -2147483648;
        
        int pre_sum = nums[0];
        int cur_sum = nums[0];
        int max_sum = nums[0];

        for(int i = 1; i<nums.size();i++){
            /*
            cur_sum 当前和
            max_sum 当前最大和
            pre_sum 之前i-1和

            当pre_sum < 0时，max(nums[i], pre_sum + nums[i]) = nums[i],
            相当于抛弃前面所包含的子序列

            动手模拟更清晰
            */

            cur_sum = max(nums[i], pre_sum + nums[i]);
            max_sum = max(cur_sum, max_sum);
            pre_sum = cur_sum;
            /*代码可以更简洁：
            cur_sum = max(nums[i], cur_sum + nums[i]);
            max_sum = max(cur_sum, max_sum);
            */
        }

        return max_sum;
    }
};

1.1.4 Leetcode官方解答

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int pre = 0, maxAns = nums[0];
        for (const auto &x: nums) {
            pre = max(pre + x, x);
            maxAns = max(maxAns, pre);
        }
        return pre;
    }
};

还是手动模拟一边算法最好理解

1.2 方法二 分治

1.3 查缺补漏

1.3.1 线段树

1.3.2 后无效性的理解

---

【第二题】 152. 乘积最大子数组

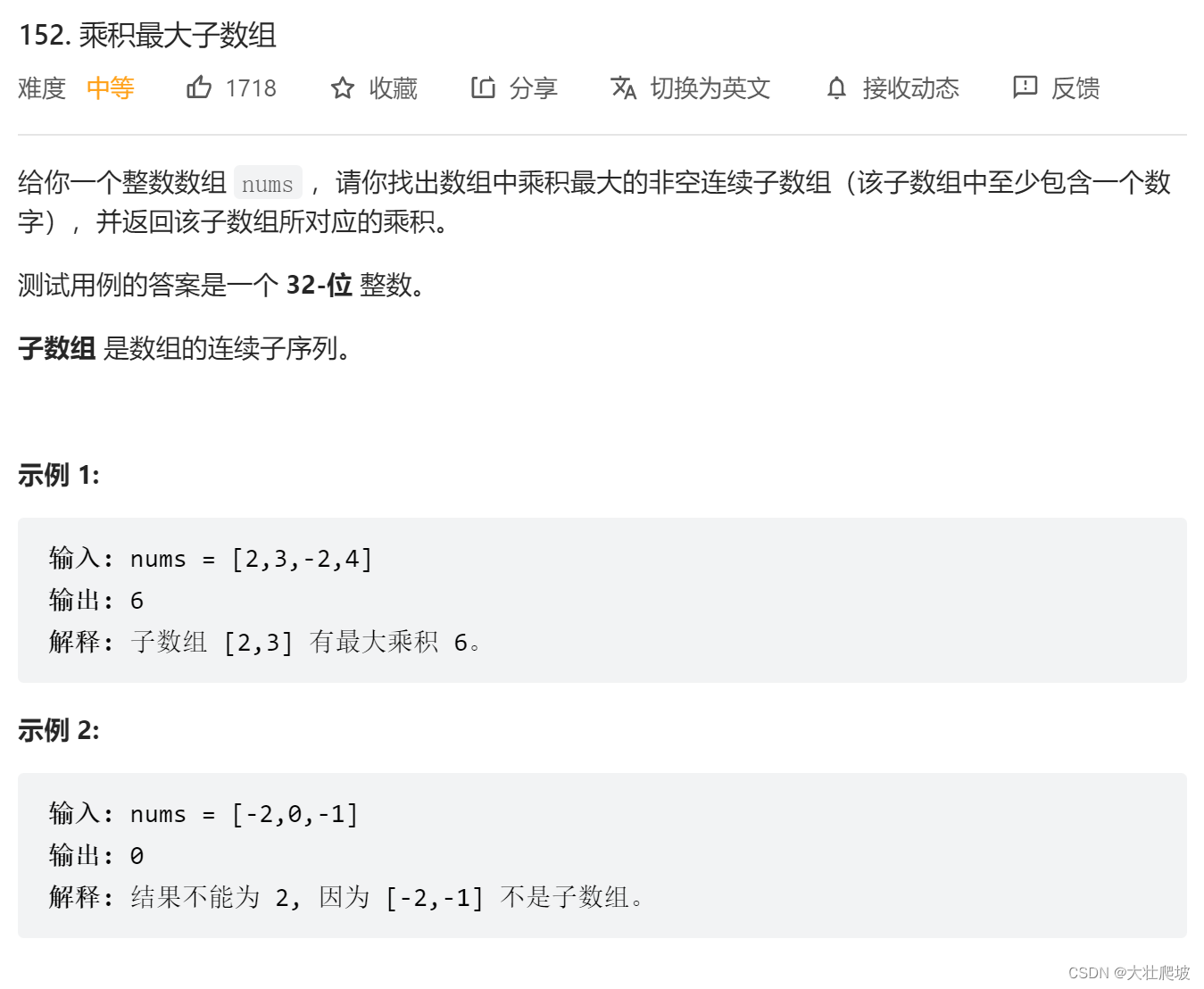
2.1 思路

根据上一题的经验，很容易想到下面的状态转移方程。但是在本题显然是不成立的。

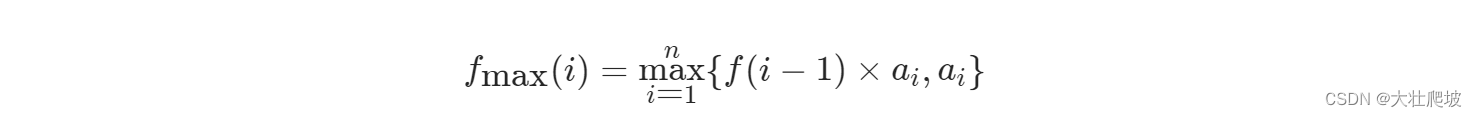
本题重要特征：当前位置的最优解未必是由前一个位置的最优解转移得到的。（对比上一题进行理解）

2.1.1 算法

根据当前位置的正负性进行分类讨论：

维护两个函数：

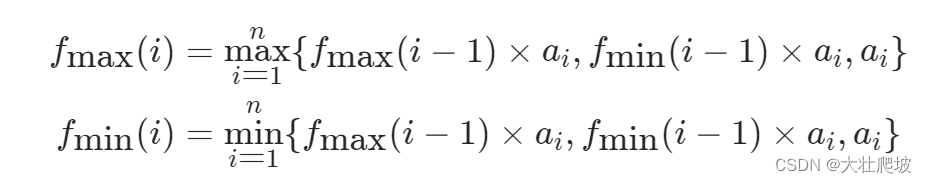
fmin(i)：它表示以第 i个元素结尾的乘积最小子数组的乘积
fmax(i)：它表示以第 i个元素结尾的乘积最大子数组的乘积

2.1.2 代码

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int maxAns = nums[0];
        int minF = nums[0];
        int maxF = nums[0];
        for(int i = 1; i< nums.size();i++){
            int x = nums[i];
            // 设置两个变量preMax和preMin保存上一轮的maxF和minF
            // 不然在minF中的maxF会由于在当轮的修改而导致答案出错
            int preMax = maxF, preMin = minF;
            
            maxF = max(preMax * x, max(x, preMin * x));
            minF = min(preMin * x, min(x, preMax * x));
            maxAns = max(maxAns, maxF);
        }
        return maxAns;
    }
};

---

【第三题】