3 遍历—哈密顿通路/回路/竞赛图

Zx-Chen

已于 2024-11-15 11:09:46 修改

阅读量1.1k

点赞数 6

分类专栏：图论基础文章标签： c++ 算法图论

于 2024-11-15 11:05:57 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_45034895/article/details/143789866

版权

图论基础专栏收录该内容

18 篇文章

订阅专栏

图论 —— 图的遍历 —— 哈密顿问题_哈密顿遍历-优快云博客

哈密尔顿回路总结 - jianzhang.zj - 博客园 (cnblogs.com)

语雀版本

1 概念

1.1 哈密顿通路

存在一条路径，访问了所有顶点，且每个顶点只访问一次。

1.2 哈密顿回路

存在一个回路，访问了所有顶点，每个顶点只访问一次。

1.3 竞赛图

是有向图

竞赛图的每一对顶点 u和v，要么存在从 u 指向 v 的有向边，要么存在从 v 指向 u 的有向边，但不会同时存在两条边。

n>=2的竞赛图存在哈密顿通路（数学归纳法可以证明）

2 ore定理-哈密顿通路的充分条件

在这里插入图片描述

证明见链接2

3 Dirac定理-哈密顿回路的充分条件

证明：

ore定理的证明过程中，推导出当某条路径的顶点数k小于n时，这k个顶点必能形成哈密顿回路。

根据这一点，当k=n-1时，也是有哈密顿回路的。此时可以得到对于这个图的任意的n-1个点，都有任意不相邻的u和v，且deg(u)+deg(v)>=n-1，，则必能推导出存在哈密顿回路。得证。

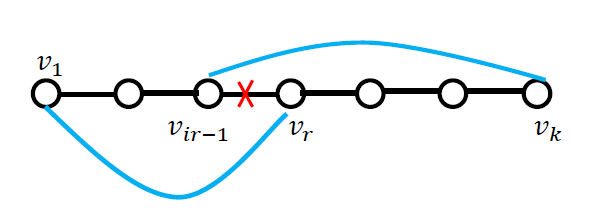
这个证明中有个很有用的信息：如果能够得到一条哈密顿回路，则肯定可以找到两个相邻的点，其中vir-1是vk的邻居，vr是v1的邻居，可以因此得到一条哈密顿回路。

4 例子

4.1 dfs得到无向图的哈密顿回路

用dfs搜索。

#include <iostream>
#include <vector>
#include <cstring>

using namespace std;

const int N = 101;

int n, m;                // n: 顶点数, m: 边数
vector<int> adj[N];      // 邻接表表示的图
int vis[N];              // 访问标记数组
int path[N];             // 当前路径
int path_len;            // 当前路径长度

void dfs(int start, int current) {
    vis[current] = 1;               // 标记当前顶点已访问
    path[path_len++] = current;     // 将当前顶点加入路径

    if (path_len == n) {            // 如果路径长度等于顶点数，表示已访问所有顶点
        // 检查是否存在从当前顶点回到起点的边，形成哈密顿回路
        for (int neighbor : adj[current]) {
            if (neighbor == start) {
                // 输出哈密顿回路
                for (int i = 0; i < path_len; i++) {
                    cout << path[i] << " ";
                }
                cout << start << endl; // 回到起点，形成回路
                break;
            }
        }
    } else {
        // 遍历所有未访问的邻接顶点
        for (int neighbor : adj[current]) {
            if (!vis[neighbor]) {
                dfs(start, neighbor);  // 递归访问下一个顶点
            }
        }
    }

    vis[current] = 0;    // 回溯，标记当前顶点未访问
    path_len--;          // 路径长度减一
}

int main() {
    cin >> n >> m;       // 输入顶点数和边数

    int u, v;
    for (int i = 0; i < m; i++) {
        cin >> u >> v;           // 输入每条边的两个顶点
        adj[u].push_back(v);     // 无向图，双向添加边
        adj[v].push_back(u);
    }

    memset(vis, 0, sizeof(vis)); // 初始化访问标记数组

    for (int x = 1; x <= n; x++) {
        path_len = 0;            // 重置路径长度
        dfs(x, x);               // 从每个顶点出发，尝试寻找哈密顿回路
    }

    return 0;
}

4.2 Dirac得到无向图的哈密顿回路

**前提：**Dirac条件成立，如果不成立则通过这种方式不一定能找到。

过程
1 任意找两个相邻的节点 S 和 T，在其基础上扩展出一条尽量长的没有重复结点的路径，即如果 S 与结点 v 
相邻，而且 v 不在路径 S -> T 上，则可以把该路径变成 v -> S -> T，然后 v 成为新的 S。从 S 和 T 
分别向两头扩展，直到无法继续扩展为止，即所有与 S 或 T 相邻的节点都在路径 S -> T 上
    
2 若 S 与 T 相邻，则路径 S -> T 形成了一个回路

3 若 S 与 T 不相邻，可以构造出来一个回路。设路径 S -> T 上有 k+2 个节点，依次为
S, v1, v2, ..., vk, T。可以证明存在节点 vi(i属于[1, k])，满足 vi 与 T 相邻，且 vi+1 与 S相邻，
找到这个节点 vi，把原路径变成 S -> vi -> T -> vi+1 -> S，即形成了一个回路

4 到此为止，已经构造出来了一个没有重复节点的的回路，如果其长度为 N，则哈密顿回路就找到了。如果回路的
长度小于 N，由于整个图是连通的，所以在该回路上，一定存在一点与回路之外的点相邻。那么从该点处把回路
断开，就变回了一条路径，同时还可以将与之相邻的点加入路径。再按照步骤 1 的方法尽量扩展路径，则一定
有新的节点被加进来，接着回到步骤2

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

#define N 1001

using namespace std;

bool G[N][N];    // 图的邻接矩阵表示
bool vis[N];     // 访问标记数组
int ans[N];      // 保存当前路径的顶点序列

// 将数组 arr 从下标 s 到下标 t 的部分进行反转
void Reverse(int arr[], int s, int t){
    while(s < t){
        swap(arr[s], arr[t]);
        s++;
        t--;
    }
}

// Hamilton 函数，用于构造哈密顿回路
void Hamilton(int n){
    int s = 1; // 初始化，选择 1 号顶点作为起点
    int t = -1;

    // 找到与 s 相邻的一个顶点 t
    for(int i = 1; i <= n; i++){
        if(G[s][i]){
            t = i;
            break;
        }
    }

    if(t == -1){
        cout << "图不连通，无法找到哈密顿回路。" << endl;
        return;
    }

    memset(vis, false, sizeof(vis));
    vis[s] = true;
    vis[t] = true;
    ans[0] = s;
    ans[1] = t;
    int ansi = 2; // 当前路径长度

    while(true){
        // 从 t 向外扩展
        while(true){
            bool extended = false;
            for(int i = 1; i <= n; i++){
                if(G[t][i] && !vis[i]){
                    ans[ansi++] = i;
                    vis[i] = true;
                    t = i;
                    extended = true;
                    break;
                }
            }
            if(!extended)
                break;
        }

        // 将当前路径反转
        Reverse(ans, 0, ansi - 1);

        // 交换 s 和 t
        swap(s, t);

        // 从新的 t（原来的 s）继续向外扩展
        while(true){
            bool extended = false;
            for(int i = 1; i <= n; i++){
                if(G[t][i] && !vis[i]){
                    ans[ansi++] = i;
                    vis[i] = true;
                    t = i;
                    extended = true;
                    break;
                }
            }
            if(!extended)
                break;
        }

        // 如果 s 和 t 不相邻，进行路径调整
        if(!G[s][t]){
            bool adjusted = false;
            // 寻找路径中的某个位置 i，使得 ans[i] 与 t 相邻，且 ans[i+1] 与 s 相邻
            for(int i = 0; i < ansi - 1; i++){
                if(G[ans[i]][t] && G[s][ans[i+1]]){
                    // 反转 ans[i+1] 到 ans[ansi - 1] 的部分
                    Reverse(ans, i + 1, ansi - 1);
                    // 更新 t
                    t = ans[ansi - 1];
                    adjusted = true;
                    break;
                }
            }
            if(!adjusted){
                cout << "无法调整路径使得 s 和 t 相邻，无法构造哈密顿回路。" << endl;
                return;
            }
        }

        // 如果当前路径包含了所有顶点，且 s 和 t 相邻，则找到哈密顿回路
        if(ansi == n && G[s][t]){
            ans[ansi] = ans[0]; // 回到起点，形成回路
            cout << "找到哈密顿回路：" << endl;
            for(int i = 0; i <= ansi; i++){
                cout << ans[i] << " ";
            }
            cout << endl;
            return;
        }

        // 当前路径未覆盖所有顶点，寻找未访问的顶点连接
        bool found = false;
        for(int i = 0; i < ansi; i++){
            for(int j = 1; j <= n; j++){
                if(!vis[j] && G[ans[i]][j]){
                    // 找到未访问的顶点 j，与路径中的顶点 ans[i] 相邻
                    // 将路径在 ans[i] 处断开，尝试扩展
                    s = ans[i];
                    t = j;
                    vis[j] = true;
                    // 反转 ans[0..i]
                    Reverse(ans, 0, i);
                    // 将 j 加入路径
                    ans[ansi++] = j;
                    found = true;
                    break;
                }
            }
            if(found)
                break;
        }
        if(!found){
            cout << "无法找到新的未访问顶点，无法构造哈密顿回路。" << endl;
            return;
        }
    }
}

int main(){
    int n, m;
    cout << "请输入顶点数和边数（n m）：";
    while(scanf("%d%d", &n, &m) != EOF && (n || m)){
        // 初始化图
        memset(G, false, sizeof(G));
        memset(ans, 0, sizeof(ans));

        cout << "请输入每条边（u v）：" << endl;
        for(int i = 0; i < m; i++){
            int u, v;
            scanf("%d%d", &u, &v);
            if(u < 1 || u > n || v < 1 || v > n){
                cout << "输入的顶点编号超出范围！" << endl;
                return 0;
            }
            G[u][v] = true;
            G[v][u] = true; // 无向图，双向连接
        }

        // 检查 Dirac 定理条件
        bool dirac = true;
        for(int i = 1; i <= n; i++){
            int degree = 0;
            for(int j = 1; j <= n; j++){
                if(G[i][j]){
                    degree++;
                }
            }
            if(degree < n / 2){
                dirac = false;
                break;
            }
        }
        if(!dirac){
            cout << "图不满足 Dirac 定理条件，无法保证存在哈密顿回路。" << endl;
            continue;
        }

        Hamilton(n);
        cout << "请输入顶点数和边数（n m）：";
    }
    return 0;
}

4.3 竞赛图得到有向图的哈密顿通路

#include <iostream>
#include <vector>

using namespace std;

const int MAXN = 105;

int n;                    // 顶点数
int adj[MAXN][MAXN];      // 邻接矩阵，表示有向边
vector<int> ans;          // 存储哈密顿通路

// 插入顶点到路径的适当位置
void insertVertex(int vertex) {
    int len = ans.size();
    // 情况 1：如果路径末端到 vertex 存在有向边，直接添加到路径末端
    if (adj[ans[len - 1]][vertex]) {
        ans.push_back(vertex);
    } else {
        bool inserted = false;
        // 从路径的起始位置开始向后搜索
        for (int j = 0; j < len - 1; ++j) {
            // 检查 ans[j] -> vertex 和 vertex -> ans[j+1]
            if (adj[ans[j]][vertex] && adj[vertex][ans[j + 1]]) {
                // 将 vertex 插入到位置 j+1
                ans.insert(ans.begin() + j + 1, vertex);
                inserted = true;
                break;
            }
        }
        if (!inserted) {
            // 情况 3：将 vertex 插入到路径末端
            ans.push_back(vertex);
        }
    }
}

int main() {
    cin >> n;
    int m = n * (n - 1) / 2;  // 竞赛图的边数

    // 初始化邻接矩阵
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            adj[i][j] = 0;
        }
    }

    // 读取边的信息
    for (int i = 0; i < m; ++i) {
        int u, v;
        cin >> u >> v;
        adj[u][v] = 1;  // 存在从 u 到 v 的有向边
    }

    // 初始化路径，起始顶点为 1
    ans.push_back(1);

    // 逐步插入顶点构建哈密顿通路
    for (int i = 2; i <= n; ++i) {
        insertVertex(i);
    }

    // 输出哈密顿通路
    for (int i = 0; i < ans.size(); ++i) {
        if (i > 0) cout << " ";
        cout << ans[i];
    }
    cout << endl;

    return 0;
}