Python实现斐波那契数列

1.斐波那契数列背景知识

斐波那契数列指的是这样一个数列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368…
这个数列从第3项开始，每一项都等于前两项之和。
斐波那契数列的定义者，是意大利数学家列昂纳多·斐波那契（Leonardo Fibonacci）

2.斐波那契数列的递推公式和通项公式

斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

如果设F(n）为该数列的第n项（n∈N*），那么这句话可以写成如下形式：:F(n)=F(n-1)+F(n-2)，F(1)=F(2)=1。

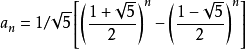
通项公式如上。

3.python程序实现。

3.1.1 递归函数

def fib(n):
    if n < 3:
        return 1
    else:
        return fib(n-1) + fib(n-2)

在python中，当使用递归形式时，需要注意的时，当使用python写的递归程序如果递归太深, 那么极有可能因为超过系统默认的递归深度限制而出现错误。一般默认递归长度在1000左右。

RecursionError: maximum recursion depth exceeded in comparison

3.1.2 栈溢出

在Python中，函数调用是通过栈（stack）这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，会导致栈溢出。

解决递归调用栈溢出的方法是通过尾递归优化，事实上尾递归和循环的效果是一样的，所以，把循环看成是一种特殊的尾递归函数也是可以的。
尾递归是指，在函数返回的时候，调用自身本身，并且，return语句不能包含表达式。这样，编译器或者解释器就可以把尾递归做优化，使递归本身无论调用多少次，都只占用一个栈帧，不会出现栈溢出的情况。
代码实现：

def fib(n,res=0,tmp=1):
	if n== 0:
	    return res
	return fib(n-1,tmp, res+tmp)

例如：fib(5) = = > fib(4, 1, 1) = => fib(3, 1 , 2) = = > fib(2 , 2 ,3) = = >fib(1, 3, 5)
= => fib(0, 5,8) = => 5
这里需要注意的是，函数内部，是按照命名参数传值的。但是当执行时，传参时按位置参数来赋值的。尾递归优化，按照我个人理解，就是将需要递归计算的值通过函数的参数来实现。不在函数内部通过表达式实现。以此来实现尾递归的优化。
或者我们可以手动来设置，

import sys
sys.setrecursionlimit(1000000) #括号中的值为递归深度

但是当我设置了之后，这个数字是非常大的。运行结果出来的也非常慢。

3.2 for循环

def fib(n):
	    f1 = f2 = 1
    for k in range(1, n-1):
        f1, f2 = f2, f2 + f1
    return f2

当然while循环同样可以实现上述的函数定义。

3.3 通项公式

def fib2(n):
    a = (1 + math.sqrt(5)) / 2
    b = (1 - math.sqrt(5)) / 2
    num_n = (1 / math.sqrt(5)) * (a ** n - b ** n)
    return int(num_n)

这种通项公式的写法复杂。而且需要对浮点型数据进行数据转换。同样会出现栈溢出的情况。

以上资料大部分来自于，和自己的一点整理。如有错误，烦请回复更正。