机器学习笔记-Task02-朴素贝叶斯

1.贝叶斯原理

贝叶斯原理是一个数学基础，人们利用该原理，设计出了贝叶斯分类器，而朴素贝叶斯是这类分类器中的一种形式。三者之间的关系，如下图所示。

　　因此为了弄懂朴素贝叶斯，需要从贝叶斯原理入手。

1.1相关概念

贝叶斯原理是为求解“逆向概率”问题而生的。为了介绍“逆向概率”，我们先来看看与之相对立的“正向概率”。

1.1.1正向概率

我们在高中在学概率时，都做过计算从盒子中任意取出一个球，是红球或黑球的概率。【一个袋子里5个球， 3个黑球，2个白球，我随便从里面拿出一个，问，是黑球的概率？。这时候，立即答：3/5。】该问题，就是一个正向概率问题。是站在上帝视角，了解问题的全貌之后作出的判断。

1.1.2逆向概率

But, 如果我们事先只知道，袋子里不是黑球就是白球，并不知道各自有多少个，而是通过我们摸出的球的颜色，我们能判断出袋子里黑白球各自多少个来吗？ 这就是逆向概率了。

1.2 具体例子加深理解

理解了上述概念，那么接下来通过一个具体的例子，通过计算过程，帮助我们进一步理解贝叶斯原理是如何求解“逆向概率”的。
【以下例子，摘自AI蜗牛车“【白话机器学习】算法理论+实战之朴素贝叶斯”】

但是，如果换一下问题：你在校园里随机游走，遇到了N个长裤的人（仍然看不清性别）， 问，这N个人里面有多少个男生，多少个女生？

学过数学的都知道，可以计算出这个学校里有多少穿长裤的，然后在穿长裤的同学当中，再计算出这里面有多少女生？多少男生就OK啦。

让我们开始动起笔来一起计算吧：
假设，学校里面有M个人。
则：
1.男生人数=MP（男），女生人数=MP(女)
2.计算一下男生里面有多少穿长裤 的，女生里面有多少穿长裤的。
（1）男生里面穿长裤的人数=男生人数xP(穿长裤|男生)【这是一个条件概率，哈哈，又是一个知识点，其读作：在该同学是男生的情况下，他穿长裤 概率，P(A|B)，即在B发生的条件下，A发生的概率】，从问题中可知:P(穿长裤|男生)=100%
（2）同理，女生里面穿长裤的人数= 女生人数*P(穿长裤|女生)，由题干可知，P(穿长裤|女生)=50%。
3.计算穿长裤的总人数
穿长裤的总人数=男生里面穿长裤的人数+女生里面穿长裤的人数
4.计算穿长裤的人数中，男女生的比例
穿长裤的同学中，男生的比例 =P(男|穿长裤)=$\frac{男生里面穿长裤的人数}{穿长裤的总人数}$=$\frac{P（男）\ast P(穿长裤|男生)}{P(穿长裤|男生)+P(穿长裤|女生)}$
【M可以约掉】

1.2.1 先验概率

过经验来判断事情发生的概率就是先验概率。比如上面的男生60%， 女生40%。这就是个事实，不用任何条件。再比如，南方的梅雨季是6-7月，就是通过往年的气候总结出来的经验，这个时候下雨的概率比其他时间高出很多，这些都是先验概率。

1.2.2 条件概率

事件 A 在另外一个事件 B 已经发生条件下的发生概率，表示为 P(A|B)，读作“在 B 发生的条件下 A 发生的概率”。比如上面的男生里面，穿长裤的P(长裤 | 男)，女生里面，穿长裤的人P(长裤 | 女)

1.2.3 后验概率

后验概率就是发生结果之后，推测原因的概率。比如上面的我看到了穿长裤的人， 我推测这是个男人P(男 | 长裤）还是个女人P(女 | 长裤)的概率。它属于条件概率的一种。

这里的P(男)， P(女)就是先验概率；P(长裤 | 男)，P(长裤 | 女)就是条件概率；P(男 | 长裤），P(女 | 长裤)就是后验概率。

上面长裤和男女可以指代一切东西，令长裤 = A, 男=B1, 女=B2, 那么整理一下上面的公式：

这个就是伟大的贝叶斯公式，更一般的形式下：

2.朴素贝叶斯

2.1何为“朴素”

朴素贝叶斯中的朴素，代表的是该算法存在的前提，即假设。它假设每个输入变量是独立的。这是一个强硬的假设，实际情况并不一定，但是这项技术对于绝大部分的复杂问题仍然非常有效。

这里的输入变量就类似与我们上面的性别特征，因为实际问题里面，可能不仅只有性别这一列特征，可能还会有什么身高啊，体重啊，这些特征，基于这些特征再利用贝叶斯公式去做分类问题的时候，就涉及很多个输入特征了。
朴素贝叶斯做的就是，假设这些身高，体重，性别这些特征之间是没有关系的，互相不影响。那么我们算同时符合这三个特征概率的时候，就可以分开算了$P(ABC)=P(A)\ast P(B)\ast P(C）$就是这个道理了

2.2朴素贝叶斯算法

改模型主要由两类概率组成：
1.每个类别的概率$P(y)$，即实例中的男女生概率；
2.每个属性的条件概率$P(xi|yi)$，即男生穿长裤的概率等。

由贝叶斯定理可知，如果需要确定属于何种类别，则需要知道如下后验概率。

因为朴素贝叶斯算法的条件独立性假设，所以

对全部i化简得：

因为$P(x1,...,xn)$是一个给定的输入常数，即用户属于一组给定的属性，想通过该算法判断其到底属于哪一类。因此后验概率（$P(y|x1,...,xn)$）的大小与$P(y){\prod }_{i=1}^{n}P(xi|y)$呈正比，即：

因此，我们的分类规则如下：

使得$P(y){\prod }_{i=1}^{n}P(xi|y)$值最大的那一类，为最终的归属类别。

2.3 朴素贝叶斯算法的工作过程

1.从训练数据中，利用极大似然估计得到$P(y)$和$P(xi|y)$；

2.计算$P(y){\prod }_{i=1}^{n}P(xi|y)$

2.4 朴素贝叶斯算法的分类

1.高斯朴素贝叶斯

其假设特征的概率服从高斯分布

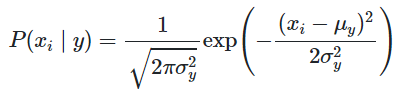
其中：
数学期望(mean)：$\mu$

方差：${\sigma }^2=\frac{\sum (X-\mu {)}^2}{N}$

【应用】主要用来处理特征量为连续变量的问题。

2.多项式朴素贝叶斯

主要用来处理离散变量问题，如文本分类。
注意
实际应用过程中，因为训练样本的原因，可能会出现零概率问题。
概率问题，就是在计算实例的概率时，如果某个量x，在观察样本库（训练集）中没有出现过，会导致整个实例的概率结果是0.

在实际的模型训练过程中，可能会出现零概率问题（因为先验概率和反条件概率是根据训练样本算的，但训练样本数量不是无限的，所以可能出现有的情况在实际中存在，但在训练样本中没有，导致为0的概率值，影响后面后验概率的计算），即便可以继续增加训练数据量，但对于有些问题来说，数据怎么增多也是不够的。这时我们说模型是不平滑的，我们要使之平滑，一种方法就是将训练（学习）的方法换成贝叶斯估计。
也可以对其进行拉普拉斯平滑处理，

其中，N表示数据集中分类标签， NiNi 表示第 ii 个属性的取值类别数，|D|样本容量， |Dc||Dc| 表示类别c的记录数量， |Dxi|c||Dxi|c| 表示类别c中第i个属性取值为 xixi 的记录数量。

将这两个式子应用到上面的计算过程中，就可以弥补朴素贝叶斯算法的这一缺陷问题

3.伯努利朴素贝叶斯算法

特征变量是布尔变量，符合 0/1 分布，在文档分类中特征是单词是否出现。
伯努利朴素贝叶斯是以文件为粒度，如果该单词在某文件中出现了即为 1，否则为 0。而多项式朴素贝叶斯是以单词为粒度，会计算在某个文件中的具体次数。而高斯朴素贝叶斯适合处理特征变量是连续变量，且符合正态分布（高斯分布）的情况。比如身高、体重这种自然界的现象就比较适合用高斯朴素贝叶斯来处理。而文本分类是使用多项式朴素贝叶斯或者伯努利朴素贝叶斯

参考资料

1.AI蜗牛车的【白话机器学习】算法理论+实战之朴素贝叶斯https://mp.weixin.qq.com/s/IXpv5QSoHM8Bx4ZQgYbm3g
2.Sklearn官方学习指南
https://scikit-learn.org/stable/modules/naive_bayes.html
3.黄博士的Github-李航04.朴素贝叶斯
https://github.com/fengdu78/lihang-code/blob/master/第04章 朴素贝叶斯/4.NaiveBayes.ipynb