剑指offer——位运算

（一）剑指Offer39. 数组中出现次数超过一半的数字

基本思路：
1.这道题最先想到也是最简单的思路就是用HashMap进行统计，或是将数组进行排序，中位数一定是超过一半的那个数字。
2.另一个方法是采用摩尔投票的方法，

（二）剑指Offer15. 二进制中1的个数

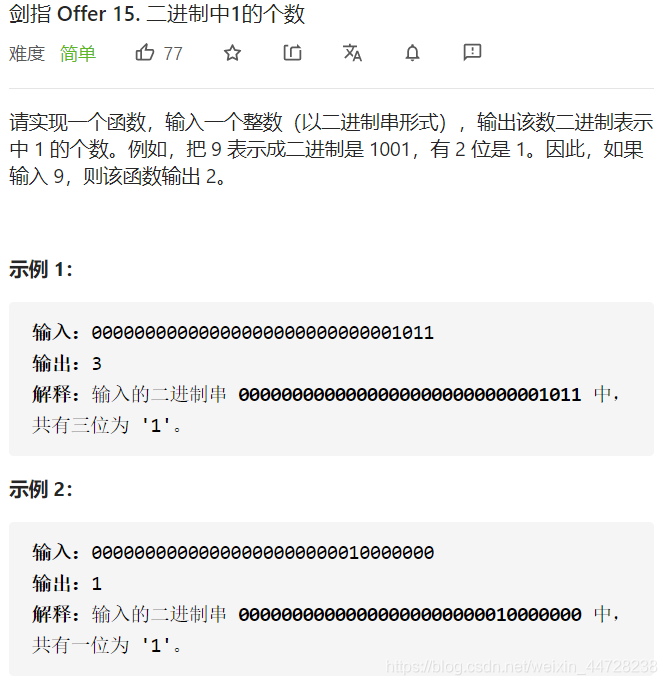
基本思路：
提取最低位，判断是否为1，并不断进行位右移。

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int total = 0;
        while(n != 0){
            if((n & 1) == 1){
                total ++;
            }
            n >>>= 1;//无符号右移
            
        }
        return total;
        
    }
}

（三）剑指 Offer 56 - I. 数组中数字出现的次数

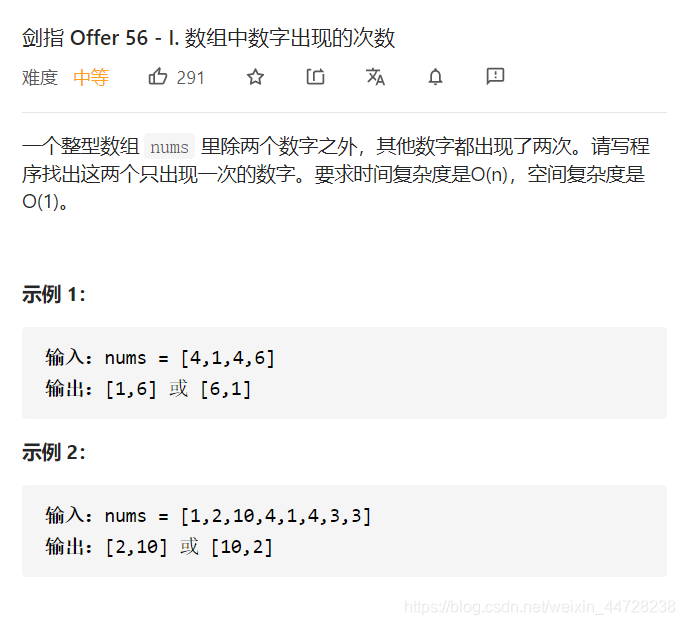
基本思路：
异或操作的结果是，两数相同为0、不同则为该数。基于这一性质，我们将所有的数异或，得到的结果是出现奇数次的数字的异或结果。
这一题中，有两个数字只出现一次，故我们需要采用一定的方法将两个数字分离开。分离方法如下：首先将所有的数字异或，得到这两个数字异或的结果；找到异或结果中为1的一个位，在这个位上，两个数字是不同的。于是我们重新对所有数字进行分组，这个位是0的数字为一组，这个数字为1的数字为一组，并将两组分别异或，得到的结果就是这两个数字。

class Solution {
    public int[] singleNumbers(int[] nums) {
        //原始题：有一个数字只出现了一次，用异或
        //现在的变形题：两个数字只出现了一次，需要找到方法把他分开
        /*将所有的数字异或，得到一个至少有一位是1的结果，这个1的位表示两个数字不同，所以根据这个为1的为是0还是1将整个数组分为两组，
        再分别异或就能得到两个数字*/
        int orr = 0;
        for(int n : nums){
            orr ^= n;
        }//得到异或结果
        int low = 1;
        while((orr & low) == 0){
            low = low<< 1;
        }//找到为1的位
        List<Integer> list1 = new ArrayList<>();
        List<Integer> list2 = new ArrayList<>();
        for(int m : nums){
            if((m & low) == 0){
                list1.add(m);
            }else{
                list2.add(m);
            }
        }
        int num1=0,num2=0;
        for(int i = 0; i < list1.size(); i++){
            num1^=list1.get(i);
        }
        for(int i = 0; i < list2.size(); i++){
            num2^=list2.get(i);
        }
        int[] res = {num1,num2};
        return res;
    }
}

（四）剑指 Offer 56 - II. 数组中数字出现的次数 II

基本思路：
1.简单的方法是进行遍历统计，存储这些数字的每一位的和，找到能被3整除的。
代码如下：

class Solution {
    public int singleNumber(int[] nums) {
        /*假设不存在这个 single number，那么 nums 中所有元素的二进制形式加起来之后，每一位必然都可以被 3 整除。因为每个数字都出现了三次，那么它们的二进制形式每一位也都出现了三次，那加起来之后每一位当然可以被 3 整除了*/
        int[] binary = new int[32];  
        for(int n : nums){
            for(int i = 0; i < 32; i++){
                binary[i] += n & 1;
                n >>= 1;
            }//最低位存在0
        }
        // for(int i=0; i<6; i++){
        //     System.out.println(i+":  "+binary[i]);
        // }
        int res = 0;
        for(int i = 31; i >= 0; i--){
            // System.out.println(i+"  "+res);
            res <<= 1;
            if(binary[i] % 3 == 1){
                res += 1;
            }
        }
        return res;
    }
}

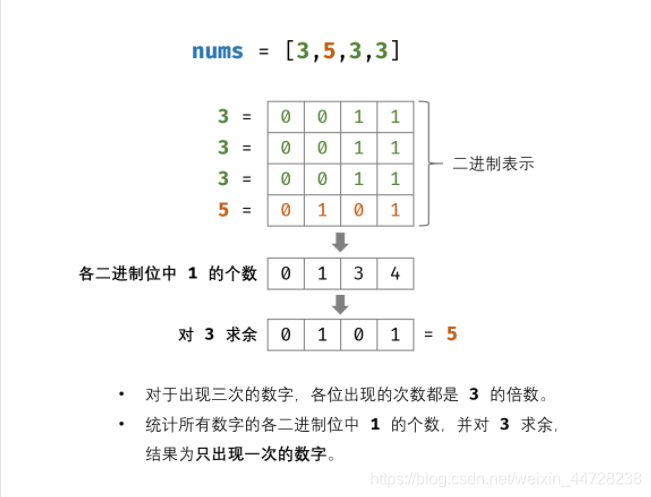
2.一个巧妙的方法是：考虑数字的二进制形式，对于出现三次的数字，各 二进制位 出现的次数都是 3 的倍数。
因此，统计所有数字的各二进制位中 1的出现次数，并对 3求余，结果则为只出现一次的数字。

（五）剑指 Offer 64. 求1+2+…+n

基本思路：
这道题基于&&运算的短路特性。A && B时，若 A 为 true，则计算并返回表达式 B 的 bool 值；若A 为 false，则直接返回 false。基于这一特性，这道题由于限制，只能采用递归方法，递归的代码如下，显然递归方法中的终止判断却无法实现。

但是，如果基于短路特性，令当n==1时，就不会执行后面的算式

class Solution {
    public int sumNums(int n) {
         /*&& 的短路特性
        A && B
        A 为 true，则计算并返回表达式 B 的 bool 值
        A 为 false，则直接返回 false
        所有的乘积，除了i
        */
        boolean x = (n > 1) && (n += sumNums(n - 1)) > 0;
        return n;
    }
}

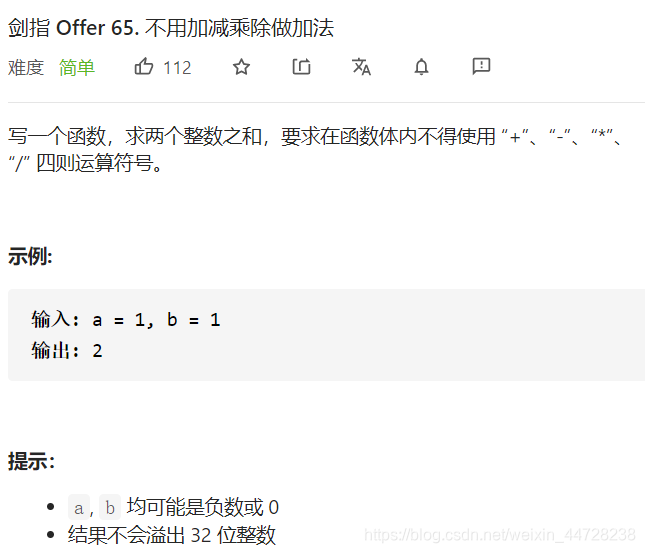
（六）剑指 Offer 65. 不用加减乘除做加法

class Solution {
    public int add(int a, int b) {
        //没有加减乘除，只能用位运算
        //位运算可以直接对数值进行，不需要转化为二进制，这都是我们便于理解才转化的
        //二进制包括：&与，|或，~非，^异或
        int c = 0;
        while(b!= 0){
            //a用于存储异或后的结果，b用于存储进位后的结果
            /* 0 1 0 0 
               1 1 1 1
               --------异或 ---------与
               1 0 1 1      0 1 0 0
               与中存在1的位置，恰好应该向前进一位
            */
            c = (a&b)<<1;
            a = a^b;
            //此时转化为c与a相加
            b = c;
        }
        return a;
    }

}