分类估计器--朴素贝叶斯算法

前言

分类算法的判定依据—目标值是离散的

一、朴素贝叶斯数学知识

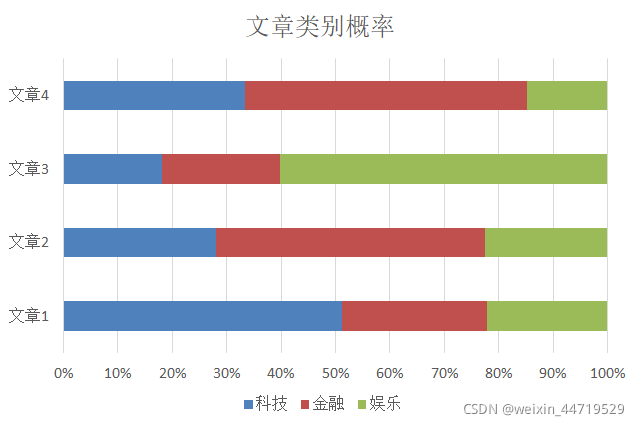
根据每篇文章所占不同类别（目标值）的比例，选择比例大的，就是该文章的目标类别。

1. 联合概率和条件概率

联合概率：包含多个条件，且所有条件同时成立的概率

记作：𝑃(𝐴,𝐵)

条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率

记作：𝑃(𝐴|𝐵)

特性：P(A1,A2|B) = P(A1|B)P(A2|B)
注意：此条件概率的成立，是由于A1,A2相互独立的结果

2.朴素贝叶斯-贝叶斯公式

公式分为三个部分：

𝑃(𝐶)：每个文档类别的概率(某文档类别词数／总文档词数)

𝑃(𝑊│𝐶)：给定类别下特征（被预测文档中出现的词）的概率

计算方法：

𝑃(𝐹1│𝐶)=𝑁𝑖/𝑁 （训练文档中去计算）

𝑁𝑖为该𝐹1词在C类别所有文档中出现的次数

N为所属类别C下的文档所有词出现的次数

𝑃(𝐹1,𝐹2,…) 预测文档中每个词的概率

3. 实例化计算

训练集统计结果(指定统计词频)：

4. 拉普拉斯平滑

问题：娱乐概率为0，这是不合理的，如果词频列表里面
有很多出现次数都为0，很可能计算结果都为零

二、代码实例化演示

1. 问题：

sklearn20类新闻分类
20个新闻组数据集包含20个主题的18000个新闻组帖子

2. 流程

1、加载20类新闻数据，并进行分割

2、生成文章特征词

3、朴素贝叶斯estimator流程进行预估

""" 
@author: Administrator 
@file: 04_朴素贝叶斯算法.py 
@time: 2021/10/21 
@desc:
1、加载20类新闻数据，并进行分割

2、生成文章特征词

3、朴素贝叶斯estimator流程进行预估
"""
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
def naviebayes():
    """
    加载20类新闻数据，并进行分割
    return: 训练集特征值，训练集目标值
    """
    # 1.获取20篇文章的数据
    news=fetch_20newsgroups(subset="all")
    # news.data:数据集的特征值
    # news.target:数据集的目标值
    # 2.根据目标值和特征值，进行划分数据：训练集特征值，训练集目标值，测试集特征值，测试集目标值
    x_train,x_test,y_train,y_test=train_test_split(news.data,news.target,test_size=0.25)

    """
    生成文章特征值，即利用TF-idF,进行特征抽取
    """
    # 1. 从训练集中抽取重要的特征词汇
    tf=TfidfVectorizer()
    x_train=tf.fit_transform(x_train)
    print(x_train)
    print(tf.get_feature_names_out())
    x_test=tf.transform(x_test)

    """
    朴素贝叶斯estimator流程进行预估
    """
    # 1. 进行朴素贝叶斯算法
    mlt=MultinomialNB(alpha=1.0)
    mlt.fit(x_train,y_train)
    # 2. 预测结果
    y_predict=mlt.predict(x_test)
    print("预测的类别是：" ,y_predict)
    # 3. 预测准确性：
    print("准确性是：", mlt.score(x_test,y_test))


    return None
if __name__=="__main__":
    naviebayes()

####################输出结果
(0, 82900)	0.04066757409925778
  (0, 18558)	0.04932446231068774
  (0, 14606)	0.04015491712404743
  (0, 23844)	0.02736935003835957
  (0, 135980)	0.02736935003835957
  (0, 59338)	0.02772103259381603
  (0, 44333)	0.027017954775042062
  (0, 36382)	0.019750636778344086
  (0, 50136)	0.02368661477290485
  (0, 121923)	0.030476757673450837
  (0, 117978)	0.025821957919404784
  (0, 143732)	0.023081128180837775
  (0, 106089)	0.01162692491469445
  (0, 116867)	0.02887904875099028
  (0, 74017)	0.027324149544884827
  (0, 49903)	0.03094110150584923
  (0, 59467)	0.03154715096242702
  (0, 80204)	0.01370454460156631
  (0, 110723)	0.02575429882515863
  (0, 66010)	0.028819283390889277
  (0, 33218)	0.04385212168209018
  (0, 30449)	0.010645033097993193
  (0, 87895)	0.03130590752301681
  (0, 134264)	0.0319041709800633
  (0, 149144)	0.03206474490638263
  :	:
  (14133, 144032)	0.06460974831099
  (14133, 108597)	0.03445275861544517
  (14133, 132153)	0.1391904871497609
  (14133, 31870)	0.049470922716430686
  (14133, 136617)	0.038864460094182415
  (14133, 34830)	0.04543728548790134
  (14133, 48545)	0.04684948625564704
  (14133, 70781)	0.04898754065975713
  (14133, 65950)	0.01810422752688703
  (14133, 134574)	0.07652487114630506
  (14133, 144711)	0.03156736876452181
  (14133, 79780)	0.0627926801990895
  (14133, 33576)	0.06521538507551371
  (14133, 104468)	0.0625644641687651
  (14133, 105029)	0.041009071921697976
  (14133, 133362)	0.018544610102790196
  (14133, 80455)	0.01845813844997291
  (14133, 133380)	0.044244051537279026
  (14133, 78017)	0.03222179060044167
  (14133, 42371)	0.022868506237760412
  (14133, 88989)	0.013835611568387645
  (14133, 105632)	0.014366423970969273
  (14133, 72870)	0.04189601280207307
  (14133, 129697)	0.013800418868204038
  (14133, 66743)	0.027600837736408076
['00' '000' '0000' ... 'ñaustin' 'óáíïìåô' 'ýé']
预测的类别是： [ 4 11  8 ...  8 17  2]
准确性是： 0.8431663837011885

三、朴素贝叶斯分类优缺点

优点：
朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。

对缺失数据不太敏感，算法也比较简单，常用于文本分类。

分类准确度高，速度快

缺点：
需要知道先验概率P(F1,F2,…|C)，因此在某些时候会由于假设的先验
模型的原因导致预测效果不佳。