Chapter1 基础算法(Ⅱ）

xiqiaong

已于 2024-12-25 15:09:57 修改

阅读量134

点赞数

文章标签：算法

于 2022-02-11 13:14:34 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_44674307/article/details/122760542

版权

一、高精度（C++要学，JAVA和Python其实没必要学）

（1）一般有四种应用场景：

A+B （A、B是大整数，长度小于等于10^6）
A-B
A×a (a<=1000小整数)
A÷a

（2）大整数如何存储？

一般用数组一位位存储；一般先存数的个位，方便进位

（3）运算

高精度加法 A+B

补充vector：

C++ vector的用法（整理）_wkq0825的专栏-优快云博客_c++ vector

#include <iostream>
#include <vector> 

using namespace std;

vector<int> add(vector<int> &A, vector<int> &B)//&? 没有也可以AC
{
	if (A.size()<B.size()) return add(B,A); //没有return会出错吧
	 
	vector<int> C;
	int t=0;
	for(int i = 0;i < A.size();i ++){
		t += A[i];
		if(i < B.size()) t += B[i];
		C.push_back(t%10);
		t /= 10;
	}
	if(t) C.push_back(t); //是否进位
	return C; 
}
int main(){
	string a, b;
	vector<int> A, B; //定义int类型的容器 
	cin >> a >> b;
	for (int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0'); //在A的最后一个向量后插入一个元素
	for (int i = b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
	
	auto C = add(A,B); //auto是指C的类型是由add的结果自动设定的
	
	for(int i = C.size()-1;i>=0;i--) cout<<C[i];
	cout << endl;
	
	return 0; 
}

高精度减法 A-B

#include <iostream>
#include <vector> 

using namespace std;

bool cmp(vector<int> &A, vector<int> &B) //a? 可以，无关 
{
	if(A.size()!=B.size()) return A.size()>B.size();
	
	for(int i = A.size()-1;i>=0;i--)
	{
		if(A[i]!=B[i]) return A[i]>B[i]; 
	}
	return true;
	
}
vector<int> sub(vector<int> &A,vector<int> &B)
{
	vector<int> C;
	for(int i=0,t=0;i<A.size();i++)
	{
		t = A[i] - t;
		if(i<B.size()) t-= B[i];
		C.push_back((t+10)%10); //注意是+10再%10
		if(t < 0) t=1; //更新进位的值。如果是直接+t呢
		else t = 0; 
	}
	while(C.size()>1&&C.back()==0) C.pop_back(); //去掉结果的前置0（存在vector的后部）
	return C; 
}
int main()
{
	string a,b;
	vector<int> A,B;
	cin >> a >> b;
	for (int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
	for (int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
	
	vector<int> C;
	
	if(cmp(A,B)) C =sub(A,B);
	else C = sub(B,A),cout << '-';
	
	for(int i = C.size()-1;i>=0;i--) cout << C[i];
	cout << endl;
	
	return 0; 
}

高精度乘法（大整数string×整数int）

#include <iostream>
#include <vector>

using namespace std;

vector<int> mul(vector<int> &A,int b)
{
	vector<int> C;
	int t = 0;
	for(int i=0;i<A.size();i++){
		t = A[i]*b+t; //注意逻辑，是先乘起来再加 
		C.push_back(t%10);
		t /= 10;
	}
	if(t) C.push_back(t);
	
	while(C.size()>1&&C.back()==0) C.pop_back();
	return C;
}
int main(){
	string a;
	int b;
	vector<int> A,C;
	cin >> a >> b;
	for(int i =a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
	
	C = mul(A,b);
	
	for(int i=C.size()-1;i>=0;i--) cout << C[i];
	cout << endl;
}

高精度除法

#include <iostream>
#include <vector>
#include <algorithm> 

using namespace std;

vector<int> div(vector<int> &A,int b,int &r)
{
	vector<int> C;
	r = 0;
	for(int i = A.size()-1;i>=0;i--)
	{
		r = r*10 + A[i];
		C.push_back(r/b); //是b不是10，与加减乘不同 
		r = r%b; 
	}
	reverse(C.begin(),C.end()); //记得颠倒，与加减乘不同 
	while(C.size()>1&&C.back()==0) C.pop_back(); 
	return C;
}
int main(){
	string a;
	int b,r;
	vector<int> A;
	cin >> a >> b;
	for(int i =a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
	
	auto C = div(A,b,r);
	
	for(int i=C.size()-1;i>=0;i--) cout << C[i];
	cout << endl << r <<endl;
}

二、前缀和与差分

1. 前缀和

有数组a1 a2 a3 ...an,则前缀和为s1 s2 s3 ...sn ,其中si=a1+a2+...+ai

为了统一操作，a0=0,s0=0

（1）计算前缀和

si=si-1+ai

（2）有何作用

计算数组在[ l , r ]之间的和，若使用常用的方法遍历，需O(n)，而使用前缀和计算只需要sr-sl-1,即O(1）

#include <iostream>

using namespace std;

const int N = 100010; //const少了会出错 
int a[N], s[N];
int main()
{
	int m, n;
	cin >> n >> m;
	for(int i = 1;i <= n;i ++){
		scanf("%d",&a[i]);
	}
	for(int i = 1;i <=n;i ++){ //前缀和的初始化 
		s[i]=s[i-1]+a[i];
	}
 	while(m--){ //区间和的计算 
 		int l,r;
 		scanf("%d %d",&l,&r);
 		printf("%d\n",s[r]-s[l-1]);
    }
    return 0;
}

补充：一般情况下scanf比cin快，可以在开头输入 " ios::sync_with_stdio(false); ” 使cin的速度与scanf类似，但此时不可使用scanf

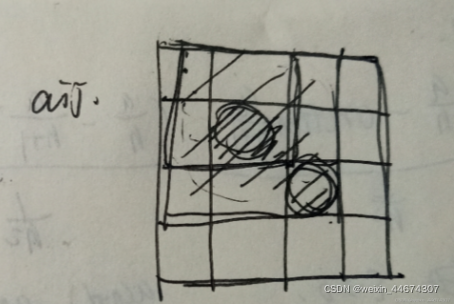
2. 二维前缀和（子矩阵的和）

（1）二维前缀和

s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j]

（2）作用

计算某子矩阵的和时，不用前缀和需要O(n^2)，利用前缀和只需要O(1)

即s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] + s[x1-1][y1-1]

3. 差分（前缀和的逆运算）

（1）有a1 a2 a3 ... an，构造b1 b2 b3 ... bn使得a是b的前缀和，b是a数组的差分

（2）作用

一般情况下给原数组[l,r]之间每个数＋c需要O(n)，而若构造了差分数组只需要O(1)，

即b[l]+c;b[r+1]-c

(3)如何构造差分数组

已知全为0的数组的差分数组也是全0。假设a数组刚开始全为0，其对应的差分数组b也全为0，要使a数组变成现在的a数组，可以看成是给a数组[i,i]区间加上ai，则只需全为0的差分数组b数组进行insert操作

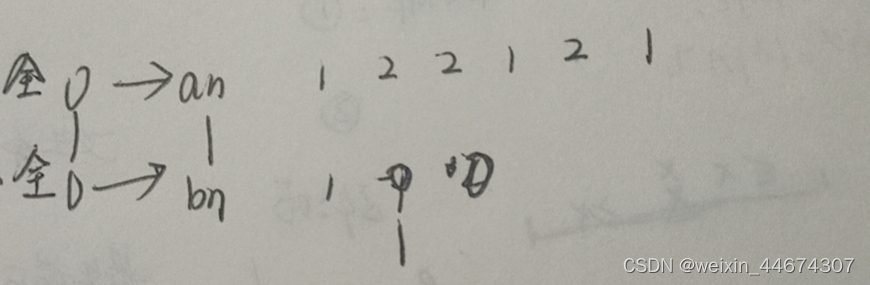
#include <iostream>

using namespace std;

const int N = 100010; //const少了会出错 
int a[N],b[N];
void insert(int l,int r,int c){
	b[l] += c;
	b[r+1] -= c;
}
int main()
{
	int n,m;
	cin >> n >> m;
	for(int i= 1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	//构造差分数组
	for(int i =1;i<=n;i++){
		insert(i,i,a[i]);
	}  
	while(m--){
		int l,r,c;
		scanf("%d %d %d",&l,&r,&c);
		insert(l,r,c);
	}
	//构造回前缀和数组 
	for(int i = i;i<=n;i++){
		a[i]=a[i-1]+b[i];
	}
	for(int i = 1;i<=n;i++){
		cout << a[i] << ' ';
	}
    return 0;
}

4. 二维差分

（1）二维数组an，构造一个二维数组bn使bn为an的差分数组，an为bn的前缀数组

（2）作用：对an的子矩阵中的数都加上c，若不使用差分数组需O(n^2)，而借助差分数组只需O(1),即

b[x1][y1] +=c;
b[x1][y2+1] -= c;
b[x2+1][y1] -= c;
b[x2+1][y2+1] += c;

构造an的差分数组，方法与上文类似

#include <iostream>

using namespace std;

const int N = 1010; //const少了会出错 
int a[N][N],b[N][N];
void insert(int x1,int y1, int x2, int y2, int c){
	b[x1][y1] +=c;
	b[x1][y2+1] -= c;
	b[x2+1][y1] -= c;
	b[x2+1][y2+1] += c;
}
int main()
{
	int n,m,q;
	cin >> n >> m >> q;
	for(int i = 1;i<=n;i++){
		for(int j =1;j<=m;j++){
			scanf("%d",&a[i][j]);
		}
	}
	//构造差分数组
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			insert(i,j,i,j,a[i][j]);
		}
	} 
	while(q--){
		int x1,y1,x2,y2,c;
		scanf("%d %d %d %d %d",&x1,&y1,&x2,&y2,&c);
		insert(x1,y1,x2,y2,c);
	}
	for(int i =1;i<=n;i++){
		for(int j=1;j<=m;j++){
			b[i][j] = b[i][j-1] + b[i-1][j] - b[i-1][j-1] +b[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			printf("%d ",b[i][j]);
		}
		printf("\n");
	}
    return 0;
}